5.3　判别分析

在生产、科研和日常生活中经常遇到需要根据事物的各种特性（测量指标）来判别其类别的问题．如对所采集的某植物的标本，根据对某花瓣、花萼等指标的测量判断它属于那个品种．一般地，若研究对象已给定用某种方式划分的若干类型（类别）的观测资料，希望构造一个或多个判别函数，能由此函数对新的未知其属性的总体的样品做出判断，从而确定该样品属于已知类型中的哪一类，这类问题属于判别分析．判别分析的方法有距离判别法、贝叶斯判别法、费歇尔判别法、最大似然法、逐步判别法等，本书仅以距离判别法为例说明判别分析法在数学建模中的应用．

5.3.1　距离判别

下面仅就两个总体的距离判别方法进行介绍．

“距离”是多维数据分析中的一个重要概念，许多多维数据分析方法是建立在距离概念基础上的，对于p 维空间中的两个点

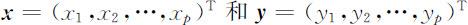
最常见的距离是欧氏距离，即

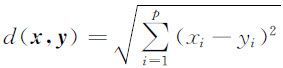
在判别分析中直接采用欧氏距离是不甚合适的，其原因是没有考虑总体分布的分散性信息．判别分析中通常采用Mahalanobis距离，简称马氏距离．首先给出马氏距离的定义．

（1）设 x，y 是来自均值向量为 μ 、协方差矩阵为 Σ 的总体G 的两个样品．则 x，y 之间的马氏平方距离是

又定义 x 与总体G 的马氏平方距离是

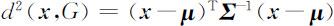
（2）设有两个总体G ₁ 和G ₂ ，其均值向量分别是 μ ₁ 和 μ ₂ ，G ₁ 和G ₂ 的协方差矩阵相等，皆为 Σ ，则总体G ₁ 和G ₂ 间的马氏平方距离是

这样，设 x 和 y 是来自均值向量为 μ 、协方差矩阵为 Σ 的总体G 的两个样品．则 x，y 之间的马氏距离是

x 至总体G 的马氏距离是

马氏距离满足距离的三个基本性质：设 x，y，z 是来自总体G 的三个样品，则

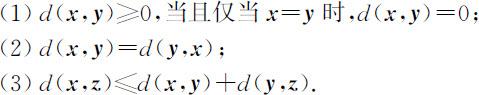
下面介绍两个总体的距离判别准则．

设G ₁ ，G ₂ 是两个不同的p 维已知总体，G ₁ 的均值向量是 μ ₁ ，协方差矩阵是 Σ ₁ ；G ₂ 的均值向量是 μ ₂ ，协方差矩阵是 Σ ₂ ．设x ＝（x ₁ ，x ₂ ，…，x_p ）^T 是一个待判样品，距离判别准则为

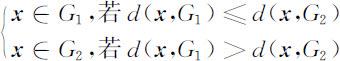
即当 x 到G ₁ 的马氏距离不超过到G ₂ 的马氏距离时，判定 x 来自G ₁ ；反之，判定 x 来自G ₂ ．

我们在特殊情况下对马氏距离判别准则的合理性给出解释．

设G ₁ 是正态总体N_p （ μ ₁ ， Σ ），G ₂ 是正态总体N_p （ μ ₂ ， Σ ），G ₁ 的概率密度

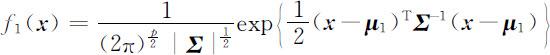
G ₂ 的概率密度

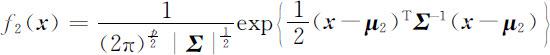
两个总体的协方差矩阵相等，皆为 Σ ，对于新样品 x ，要判别 x 属于哪个总体．根据统计学似然比准则，很自然应将 x 判归在该样品观测值处于概率密度较大的那个总体，即有下列判别准则：

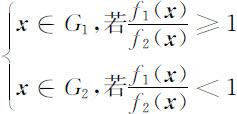
而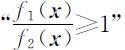 的充分必要条件是

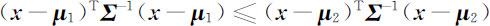
即

因此，当两总体G ₁ ，G ₂ 为正态总体且其协方差矩阵相等时，采用马氏距离判别准则与似然比准则是一致的．

下面仅就两个总体协方差矩阵相等情况进一步讨论距离判别准则．

假设两个总体协方差矩阵相等，即： Σ ₁ ＝ Σ ₂ ＝ Σ

考虑样品 x 到两总体的马氏平方距离的差：

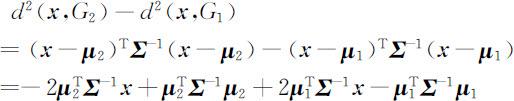
记

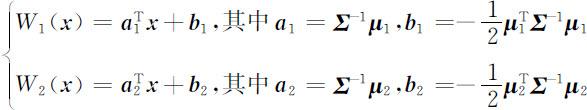
则

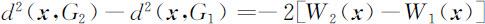
或者从另一角度看，有

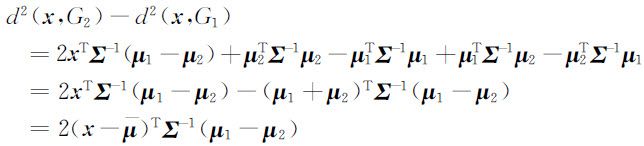
其中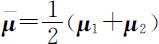 ，即 u 是两总体均值向量的平均．记

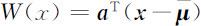
其中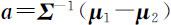 ，则

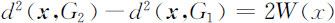
这样，距离判别准则化为

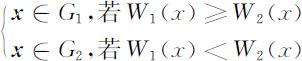
或者

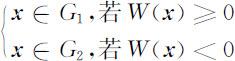
上述W ₁ （x ），W ₂ （x ）及W （x ）皆是线性判别函数．

5.3.2　判别分析建模案例

例　DNA序列分类问题 ^［17］

5.3.2.1　问题分析：根据题意，我们首先要提出一个序列的特征，然后给出它的数学表示，最后选择并构造基于这种数学表示的分类方法，对于任意一个DNA序列，反映该序列特征的方面有两个：

1．碱基的含量，反映了该序列的内容；

2．碱基的排列情况，反映了该序列的形式．

5.3.2.2　基于碱基含量特征分类的模型

首先，我们考虑采取序列中的A，G，T，C 的含量百分比作为该序列的特征．这样的抽取特征的方法具有其生物学的意义，前面提到过，在不用于编码蛋白质的序列片段中，A 和T 的含量特别多些，因此某些碱基特别丰富作为特征去研究DNA序列的结构是具有可行性的．将序列中的A，G，T，C 的含量百分比分别记为na，ng，nt，nc 则得到一组表征该序列的四维向量（na，ng，nt，nc ）．考虑到（na，ng，nt，nc ）线性相关（na ＋ng ＋nt ＋nc ＝1），所以我们采用简化的三维向量（na，nt，ng ）来进行计算，对于标号为i 的序列，记它们的特征向量为 X _i ．显然，任意序列的特征向量与一个三维空间的点对应．

一般的判别问题为：设k 个类别G ₁ ，G ₂ ，…，G_k ，对任意一个属于G_i 类样品x ，其特征向量的值都可以获得．现给定一个由已知类别的一些样品x ₁ ，x ₂ ，…，x_n 组成的学习样本，要求对一个来自这k 个类别的某样品x ，根据其特征向量的值作出其所属类别的判断．

在本题DNA序列分类中，k ＝2，G ₁ ＝A，G ₂ ＝B ，特征向量x 是三维的，学习样本中共包含n ＝20个样本，其中10个属于A ，10个属于B ，我们分别采用了欧氏距离（Euclid）分类模型，马氏距离（Mahalanobis ）分类模型和Fisher判别模型来对序列样本分类．

（1）欧氏距离（Euclid）分类模型

在欧氏距离（Euclid）分类模型中，把每个样本视为三维空间的一个点，以其到不同几何中心的欧氏距离作为判据，具体算法如下：

①计算属于A 类与属于B 类的10个样本点的各自的几何中心：

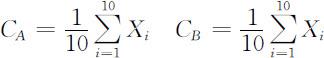
②对于给定的样本点X_i ，分别计算该点到C_A 的欧氏距离D_A ＝|X_i -C_A |，以及该点到C_B 的欧氏距离D_B ＝|X_i -C_B |．

③判别准则如下：

a．若D_A <D_B ，则将X_i 点判为A 类；

b．若D_A >D_B ，则将X_i 点判为B 类；

c．若D_A ＝D_B ，则将X_i 点判为不可判类．

④判别结果：

用上述算法对已知学习样本A ₁ ～A ₂₀ 进行分类，结果是除了A ₄ 被错误的分到了B 类，其余的19个样本全部正确，分类准确率达到95％．

用上述算法对未知的人工序列A ₂₁ ～A ₄₀ 进行分类，得到的结果是：

A 类，22，23，25，27，29，30，32，34，35，36，37，39；B 类：21，24，26，28，31，33，38，40

同样可用上述算法对未知的自然序列N ₁ ～N ₁₈₂ 进行分类，得到的结果（略）．

用欧氏距离作为判据虽然简便直观，但存在着明显的缺陷：从概率统计的角度来看，用欧氏距离描述随机点之间的距离并不好，因此当待分类样本是随机样本时且具有一定的统计性质时，这个模型并不能很好地描述两个随机点之间的接近程度．

（2）马氏距离（Mahalanobis ）分类模型

为了克服采用欧氏距离的缺陷，我们采用马氏距离来代替欧氏距离，改进后的算法如下：设：三维总体G 的均值 μ ＝（μ ₁ ，μ ₂ ，μ ₃ ）^T ，协方差矩阵为非奇异阵 V _3×3 ，则三维样本 X 到总体G 的马氏距离为：

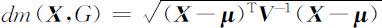
其中未知的μ 可用学习样本的均值来代替，协方差矩阵 V 可用学习样本的样本协方差矩阵来代替．

将马氏距离用于判别模型，遵循判据如下：

1．若dm （ X ，A ）<dm （ X ，B ），则判定x 为A 类；

2．若dm （ X ，A ）>dm （ X ，B ），则判定x 为B 类；

3．若dm （ X ，A ）＝dm （ X ，B ），则判定x 为不可判类．

用上述算法对已知学习样本A ₁ ～A ₂₀ 进行分类，结果是除了A ₄ 被错误的分到了B 类，其余的19个样本全部正确，分类准确率达到95％．

用上述算法对未知序列A ₂₁ ～A ₄₀ 进行分类，得到的结果是：

A 类：22，23，25，27，29，30，32，33，34，35，36，37

B 类：21，24，26，28，31，38，39，40

用上述算法可对未知的自然序列N ₁ ～N ₁₈₂ 进行分类，得到的结果．

（3）Fisher判别模型

在多维空间里分类方法不仅仅是距离分类法一种，常用的Fisher分类法就是另一种基于几何特性的分类法．在距离判别模型中，三维空间的样品 X 被映射为一维的距离d 来做判别，Fisher分类法的思想也是把三维空间的样本映射到一维的特征值 y ，并依据 y 来进行判别，具体的做法是先引入一个与样本同维的待定量μ ，再将 y 取为 X 坐标的线性组合y ＝ μ ^T X ，而μ 的选取要使同一类别产生的y 尽量靠拢，不同类别产生的 y 尽量拉开，这样，我们便可将样品 X 到某一类G 的距离定义为 y ＝ μ ^T X 与 y _c ＝ μ ^T c 之间的欧氏距离：

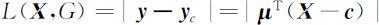
其中c 为G 的几何中心．

Fisher分类的判据为：

1．若L （ X ，A ）<L （ X ，B ），则判定 X 为A 类；

2．若L （ X ，A ）>L （ X ，B ），则判定 X 为B 类；

3．若L （ X ，A ）＝L （ X ，B ），则判定 X 为不可判类．

根据对 μ 的要求，Fisher提出了比较有效的选择算法，利用该算法，从学习样本中获得：

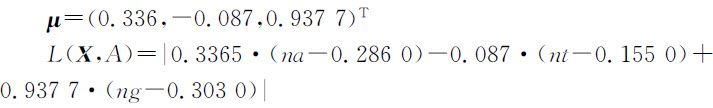
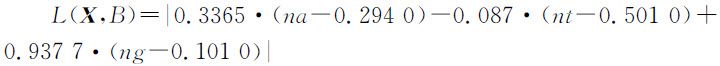
用上述算法对已知学习样本A ₁ ～A ₂₀ 进行分类，结果是除了A ₄ 被错误的分到了B 类，其余的19个样本全部正确，分类准确率达到95％．

用上述算法对未知序列A ₂₁ ～A ₄₀ 进行分类，得到的结果是：

A 类：22，23，25，27，34，35，36，37

B 类：21，24，26，28，30，31，32，33，38，39，40

用上述算法对未知的自然序列N ₁ ～N ₁₈₂ 进行分类，可以得到分类的结果．

5.3.3　三种距离分类模型的比较

这三种模型在分类结果上有一定的区别，对于序列A ₃₀ A ₃₂ A ₃₃ 及A ₃₉ ，三种方法给出了不同结果，见表5.8．