3.2　简单优化模型建模与案例分析

工厂定期订购原料，存入仓库供生产之用；车间一次加工出一批零件，供装配线每天生产之需；水库在雨季蓄水，用于旱季的灌溉和发电．显然，这些情况下都有一个存贮量多大才合适的问题．存贮量过大，存贮费用太高；存贮量太小，会导致一次性订购费用增加，或不能及时满足需求．

这里，讨论两个简单的存贮模型：不允许缺货模型和允许缺货模型．

1．不允许缺货模型

先考察这样一个问题：配件厂为装配线生产若干种部件，轮换生产不同的部件时因更换设备要付生产准备费（与生产数量无关），同一部件的产量大于需求时因积压资金、占用仓库要付贮存费．

已知某一部件的日需求量为100件，生产准备费5000元，贮存费每日每件1元．如果生产能力远大于需求，并且不允许出现缺货，试安排该产品的生产计划，即多少天生产一次（称为生产周期），每次产量多少，可使总费用最小．

（1）分析

生产周期短、产量少，会使周期内总贮存费小，而每天的准备费大；而周期长、产量多，会使周期内总贮存费大，每天的准备费小．所以，必然存在一个最佳周期，使得总费用最小．要使总费用最小，也就是使得周期内每天的平均费用最低．

（2）模型假设

为了处理的方便，考虑连续模型，即设生产周期T 和产量Q 均为连续量．根据问题性质作如下假设：

①产品每天的需求量为常数r ；

②每次生产准备费为c ₁ ，每天每件产品贮存费为c ₂ ；

③生产能力为无限大（相对于需求量），当贮存量降到零时，Q 件产品立即生产出来供给需求，即不允许缺货．

（3）模型建立

将贮存量表示为时间t 的函数q （t ），t ＝0生产Q 件，贮存量q （0）＝Q，q （t ）以需求速率r 递减，直到q （t ）＝0，如图3.1，显然有

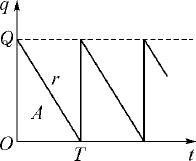
图3.1　不允许缺货模型的贮存量q （t ）

一个周期内的贮存费是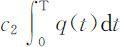 ，其中积分恰等于图3.1中三角形A 的面积 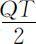．因为一个周期的准备费是c ₁ ，再注意到（3.2.1）式，得到一周期的总费用为

于是每天的平均费用是

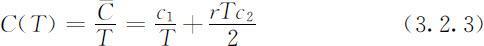
（3.2.3）式为这个优化模型的目标函数．

（4）模型求解

求T 使（3.2.3）式的C 最小．容易得到

代入（3.2.1）式可得

由（3.2.3）式算出最小的总费用为

（3.2.4）、（3.2.5）式是经济学中著名的经济订货批量公式（EOQ公式）．

（5）结果解释

由（3.2.4）、（3.2.5）式可以看到，当准备费c ₁ 增加时，生产周期和产量都变大；当贮存费c ₂ 增加时，生产周期和产量都变小；当需求量r 增加时，生产周期变小而产量变大．这些定性结果都是符合常识的，当然，（3.2.4）、（3.2.5）式的定量关系（如平方根、系数2等）凭常识是无法猜出的，只能由数学建模得到．

用得到的模型计算本节开始的问题：以c ₁ ＝5000，c ₂ ＝1，r ＝100代入（3.2.4），（3.2.6）式可得到T ＝10天，C ＝1000元．

（6）敏感性分析

讨论参数c ₁ ，c ₂ ，r 有微小变化时对生产周期T的影响．用相对该变量衡量结果对参数的敏感程度，T 对c ₁ 的敏感度记作S （t，c ₁ ），定义为

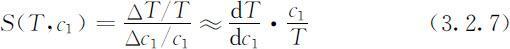
由（3.2.4）式容易得到S （T，c ₁ ）＝1/2，即c ₁ 增加1％，T增加0.5％．作类似的定义并可得到S （t，c ₂ ）＝-1/2，S （t，r ）＝-1/2，即c ₂ 或r 增加1％，T 减少0.5％．c ₁ ，c ₂ ，r有微小变化时对生产周期T 的影响是很小的．

考察用户向供方订货的情况：如果订货时要付一笔订货费（与订货量无关），贮存费和用户需求量的假设与上面模型一样，并且当贮存量降到零时所订货物立即到达，那么只需将订货费类比于生产准备费，就会得到完全相同的模型，实际上，EOQ公式原本就是针对这种订货情况的．

2．允许缺货模型

在某些情况下用户允许短时间的缺货，虽然会造成一定的损失，但是如果损失费不超过缺货导致的准备费和贮存费的话，允许缺货就应该是可以采取的策略．

（1）模型假设

下面讨论一种简单的允许缺货模型：不允许缺货模型的假设1，2不变，假设3改为：

生产能力为无限大（相对于需求量），允许缺货，每天每件产品缺货损失费为c ₃ ，但缺货数量需在下次生产（或订货）时补足．

（2）模型建立

因贮存量不足造成缺货时，可认为贮存量函数q （t ）为负值，如图3.2周期仍记作T ，每周期初的贮存量为Q ，当t ＝T ₁ 时，q （t ）＝0，于是有

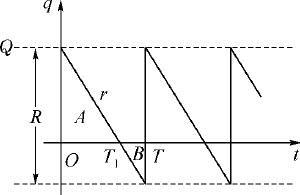
图3.2　允许缺货模型的贮存量q （t ）

在T ₁ 到T 这段缺货时段内需求率r 不变，q （t ）按原斜率继续下降．由于规定缺货量需补足，所以在t ＝T 时，数量为R 的产品立即到达，使下周期初的贮存量恢复到Q ．

与建立不允许缺货模型时类似，一个周期内的贮存费是c ₂ 乘以图3.2中三角形A 的面积，缺货损失费则是c ₃ 乘以图3.2中三角形B 的面积．计算这两块面积，并加上准备费c ₁ ，得到一周期的总费用为：

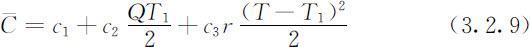
利用（3.2.8）式将模型的目标函数（每天的平均费用）记作T 和Q 的二元函数：

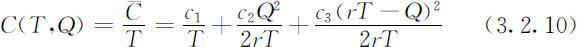
（3）模型求解

利用微分法求T 和Q 使C （T，Q） 最小，令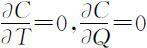 ，可得（为了和不允许缺货模型相区别，最优解记作T ′，Q ′）

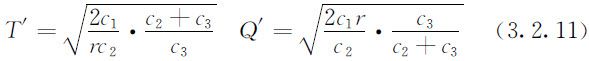
注意每周期的供货量R ＝rT ′，有

记

与不允许缺货模型的结果（3.2.4）、（3.2.5）式比较不难得到

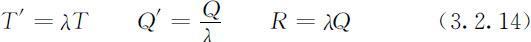
（4）结果解释

由（3.2.13）式，λ >1，故（3.2.14）式给出T ′>T，Q ′<Q，R >Q ，即允许缺货时周期及供货量应增加，周期初的贮存量减少．缺货损失费c ₃ 越大（相对于贮存费c ₂ ），λ 越小，T ′越接近T，Q ′、R 越接近Q ．考虑到c ₃ 的意义，可知当c ₃ →∞时λ →1，于是T ′→T，Q ′→Q，R →Q ，这说明：不允许缺货模型可视为允许缺货模型的特例．