表5.1　方差分析表

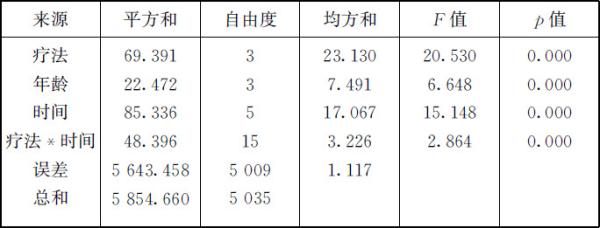
由方差分析表可知：观察变量log（CD4count＋1）的总变差可以分解为三大部分：

（1）各控制变量独立作用造成的变差．不同疗法造成的变差平方和为69.391，均方为23.130，不同年龄段造成的变差平方和为22.472，均方为7.491，不同测量时间造成的变差平方和为85.336，均方为17.067，可见，疗法种类对CD4浓度的影响要大于年龄和测量时间对CD4的影响．再从它们的F 值看，分别为20.530，6.648，15.148，对应的p 值都为0.000，说明年龄、疗法、时间对CD4浓度都有显著影响．

（2）疗法和时间的交互作用造成的变差．这里，不同疗法和不同时间交互作用造成的CD4浓度变差平方和为48.396，均方3.226，F 值2.864，p 值为0.000，说明不同疗法与不同测量时间的交互作用对CD4浓度有显著的影响．

（3）其他随机因素

通过方差分析，我们可知三个控制变量对疗效的影响程度．

例2　高等学校学费问题 （CUMCM2007年B题）

《高等学校学费问题研究》中要求分析高校学费对城乡居民的承受能力的影响，如果单纯从学费收入比数据分析，仅能反映家庭的学费负担情况，但不能说明城乡差异，因此可以用方差分析的方法进行分析建模．

根据题中给出的2003年我国高校平均学费占家庭年收入的比例的数据，用统计软件SPSS进行初步数据处理和分类，可以得到基本的描述性统计量和学费占收入比例的城乡差距状况．将控制变量设为城镇家庭和农村家庭，建立方差分析模型，可以得到以下结果：平均而言，对于城乡居民家庭来说，2003年高校学费平均占家庭收入的19.34％，而对于农村居民家庭而言，却占到43.34％．另外，在等方差假设条件下的F 检查概率值P ＝0.07<0.53，拒绝原假设，这说明了两类家庭的承受能力存在显著差异，城镇家庭的变异系数为0.83，远远小于农村家庭的变异系数4.65，说明农村家庭承受学费的压力更大且波动范围广泛．