图6.3 金属资源开发的综合判断
6.1.3 层次分析建模方法与步骤
下面以旅游地选择问题来说明这类决策问题的层次分析法的建模与求解步骤.
运用层次分析法构造系统模型时,大体可以分为以下四个步骤:
(1)建立层次结构模型.通过分析系统中各因素之间的关系,建立系统的递阶层次结构,一般层次分为三层:第一层为目标层,第二层为准则层,第三层为方案层.
(2)构造判断(成对比较)矩阵.对同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造成对比较矩阵.
(3)层次单排序及其一致性检验.由成对比较矩阵计算被比较元素对于每一准则的相对权重,并进行成对矩阵的一致性检验.
(4)层次总排序及其一致性检验.计算方案层元素对系统目标合成权重和进行组合一致性检验,并进行排序.
1.确定各层次互相比较的方法——成对比较矩阵和权向量
在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不容易被别人接受,因而Saaty等人提出了构造一致矩阵法的原理,即
(Ⅰ)不把所有因素放在一起比较,而是两两相互比较;
(Ⅱ)对比时采用相对尺度,以尽可能减少性质不同的诸因素相互比较的困难,提高准确度.
假设要比较某一层n 个因素C 1 ,C 2 ,…,Cn 对上一层因素O 的影响(例如:旅游决策中,比较景色等5个准则在选择旅游地这个目标中的重要性).每次取两个因素Ci 和Cj 比较其对目标因素O 的影响,并用aij 表示,全部比较的结果用成对比较矩阵表示,即:
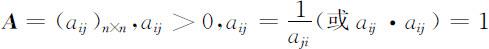
我们称具有上述性质的成对比较矩阵 A 为正互反矩阵.显然,由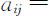
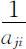 即:
即: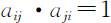 ,故有:
,故有:
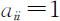
例如:在旅游决策问题中:
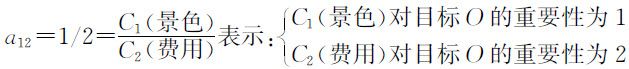
故:a 12 =1/2,即景色重要性为1,费用重要性为2.

即:景色为4,居住为1.

即:费用重要性为7,居住重要性为1.
因此有成对比较矩阵:
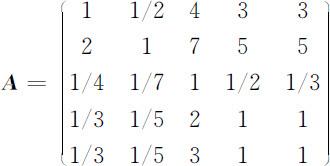
稍加分析就发现上述成对比较矩阵存在如下问题:
①即存在各元素的不一致性,例如:
既然: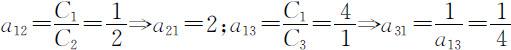
所以应该有: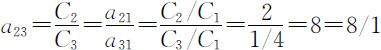
而不应为矩阵A 中的a 23 =7/1
②成对比较矩阵比较的次数要求太多.因为,n 个元素比较次数为: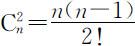 次,全部一致的要求太苛刻了.对此Saaty提出了:在成对比较出现不一致情况下,计算各因素C 1 ,…,Cn 对因素(上层因素)O 的权重方法,并确定了这种不一致的容许误差范围.我们来看成对比较完全一致的情况.为此,先给出一致性矩阵的定义及性质.
次,全部一致的要求太苛刻了.对此Saaty提出了:在成对比较出现不一致情况下,计算各因素C 1 ,…,Cn 对因素(上层因素)O 的权重方法,并确定了这种不一致的容许误差范围.我们来看成对比较完全一致的情况.为此,先给出一致性矩阵的定义及性质.
定义:设有正互反成对比较矩阵:
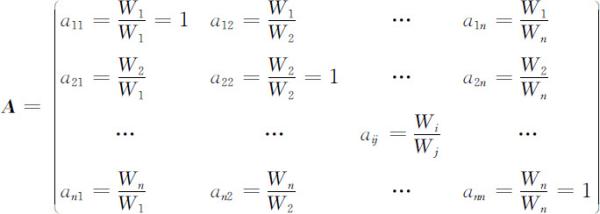
除满足:(i)正互反性:即
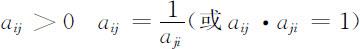
而且还满足:(ii)一致性:即
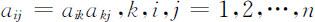
则称满足上述条件的正互反对称矩阵 A 为一致性矩阵,简称一致阵.
容易证明,一致性矩阵(一致阵)有如下性质:
性质1 A 的秩 Rank( A )=1
A 的唯一非0的特征根为n
性质2 A 的任一列(行)向量都是对应特征根n 的特征向量:

既然一致矩阵有以上性质,即n 个元素W 1 ,W 2 ,W3 ,…,Wn 构成的向量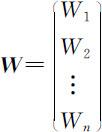 是一致矩阵 A 的特征向量,则可以把向量 W 归一化后的向量w ,看成是诸元素W 1 ,W 2 ,W3 ,…,Wn 目标的权向量,因此,可以用求 A 的特征根和特征向量的办法,求出元素W 1 ,W 2 ,W3 ,…,Wn 相对于目标O 的权向量.
是一致矩阵 A 的特征向量,则可以把向量 W 归一化后的向量w ,看成是诸元素W 1 ,W 2 ,W3 ,…,Wn 目标的权向量,因此,可以用求 A 的特征根和特征向量的办法,求出元素W 1 ,W 2 ,W3 ,…,Wn 相对于目标O 的权向量.
也就是说,假设有n 件物体M 1 ,M 2 ,…,Mn ,它们重量分别为W 1 ,W 2 ,…,Wn ,将它们两两比较重量,其比值构成一致矩阵,若用重量向量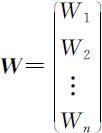 右乘 A ,则:
右乘 A ,则:

若重量向量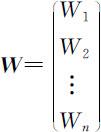 未知时,则可由决策者对物体M 1 ,M 2 ,…,Mn 之间两两比较,主观作出比值的判断,使 A 矩阵(不一定有一致性)为已知的,并记此主观判断作出的矩阵为(主观)判断矩阵 A ,并且此 A (不一致)在不一致的容许范围内,再依据 A 的特征根和特征向量 W 连续地依赖于矩阵的元素aij ,即当aij 离一致性的要求不太远时, A 的特征根 λ 和特征值(向量) W 与一致矩阵 A 的特征根λ 和特征向量 W 也相差不大的道理,由特征向量 W 求权向量w 的方法即为特征向量法,并由此引出一致性检查的方法.
未知时,则可由决策者对物体M 1 ,M 2 ,…,Mn 之间两两比较,主观作出比值的判断,使 A 矩阵(不一定有一致性)为已知的,并记此主观判断作出的矩阵为(主观)判断矩阵 A ,并且此 A (不一致)在不一致的容许范围内,再依据 A 的特征根和特征向量 W 连续地依赖于矩阵的元素aij ,即当aij 离一致性的要求不太远时, A 的特征根 λ 和特征值(向量) W 与一致矩阵 A 的特征根λ 和特征向量 W 也相差不大的道理,由特征向量 W 求权向量w 的方法即为特征向量法,并由此引出一致性检查的方法.
2.一致性检验——一致性指标:
(1)一致性检验指标的定义和确定——C·I 的定义
当人们对复杂事件的各因素,采用两两比较时,所得到的主观判断矩阵 A ,一般不可直接保证正互反矩阵 A 就是一致正互反矩阵 A ,因而存在误差(及误差估计问题).这种误差,必然导致特征值和特征向量之间的误差 及
及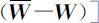 .此时就导致问题
.此时就导致问题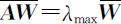 与问题 AW =nW 之间的差别(上述问题中λ max 是主观判断矩阵 A 的最大特征值, W 是带有偏差的相对权向量),这是由判断矩阵不一致性所引起的.
与问题 AW =nW 之间的差别(上述问题中λ max 是主观判断矩阵 A 的最大特征值, W 是带有偏差的相对权向量),这是由判断矩阵不一致性所引起的.
因此,为了避免误差太大,就要衡量主观判断矩阵 A 的一致性.
因为:
①当主观判断矩阵 A 为一致阵 A 时就有:
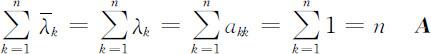 为一致阵时有:aii =1
为一致阵时有:aii =1
此时存在唯一的特征值λ =λ max =n
②当主观判断矩阵 A 不是一致矩阵时,此时一般有:λ max ⩾n
此时,应有:
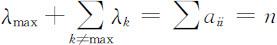
即: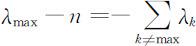
所以,可以取其平均值作为检验主观判断矩阵的准则,一致性的指标,即
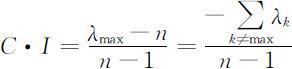
显然:
①当λ max =n 时,有:C·I =0, A 为完全一致性;
②C·I 值越大,主观判断矩阵 A 的完全一致性越差,即: A 偏离 A 越远(用特征向量作为权向量引起的误差越大);
③一般若C·I ⩽0.1,认为主观判断矩阵 A 的一致性可以接受,否则应重新进行两两比较,构造主观判断矩阵.
(2)随机一致性检验指标——R·I
实际操作时发现:主观判断矩阵 A 的维数越大,判断的一致性越差,故应放宽对高维矩阵的一致性要求.于是引入修正值R·I 来校正一致性检验指标:即定义R·I 的修正值表,如表6.1所示.
表6.1 R·I 的修正值

并定义新的一致性检验指标为: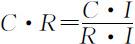
随机一致性检验指标——R·I 的解释:
为确定 A 的不一致程度的容许范围,需要确定衡量 A 的一致性指示C·I 的标准.于是Saaty又引入所谓随机一致性指标R·I ,其定义和计算过程为:
①对固定的n ,随机构造正互反矩阵 A ′,其元素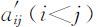 从1~9和1~1/9中随机取值,且满足
从1~9和1~1/9中随机取值,且满足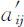 与
与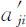 的互反性,即:
的互反性,即: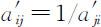 ,且
,且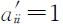 .
.
②然后再计算 A ′的一致性指标C·I ,因此 A ′是非常不一致的,此时,C·I 值相当大.
③如此构造相当多的 A ′,再用它们的C·I 平均值作为随机一致性指标.
④Saaty对于不同的n (n =1~11),用100~500个样本 A ′计算出上表所列出的随机一致性指标R·I 作为修正值表.
由随机性检验指标C·R 可知:
当n =1,2时,R·I =0,这是因为1,2阶正互反阵总是一致阵.
对于n ⩾3的成对比较阵 A ,将它的一致性指标C·I 与同阶(指n 相同)的随机一致性指标R·I 之比称为一致性比率——简称一致性指标,即有:一致性检验指标的定义——一致性比率
定义: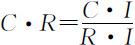
当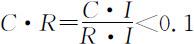 时,认为主观判断矩阵 A 的不一致程度在容许范围之内,可用其特征向量作为权向量.否则,需对主观判断矩阵 A 重新进行成对比较,构重新的主观判断矩阵 A .
时,认为主观判断矩阵 A 的不一致程度在容许范围之内,可用其特征向量作为权向量.否则,需对主观判断矩阵 A 重新进行成对比较,构重新的主观判断矩阵 A .
(3)标度——比较尺度解释(表6.2)
表6.2 标度——比较尺度解释
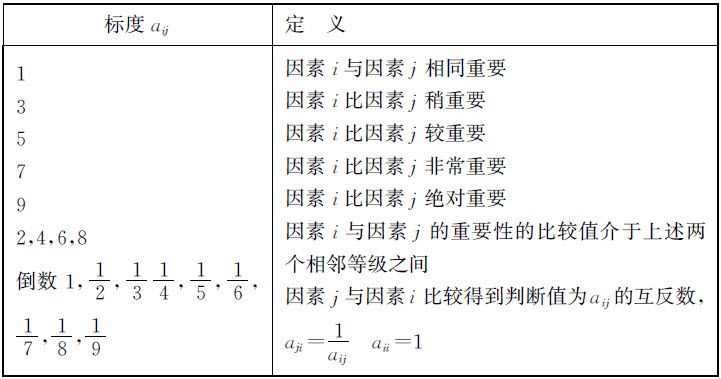
在构造正互反矩阵时,当比较两个可能是有不同性质的因素Ci 和Cj 对于上层因素O 的影响时,采用什么样的相对刻度较好,即aij 的元素的值在(1~9)或(1~1/9)或更多的数字,Saaty提出用尺度最好,即aij 取值为1~9或其互反数1~1/9,心理学家也提出:人们区分信息等级的极限能力为7±2.
6.1.4 组合权向量的计算——层次总排序的权向量的计算
根据层次分析法的基本思想,可按如下步骤计算层次总排序的权向量,即计算同一层次所有元素对最高层相对重要性的排序权值.
1.计算出下一层每个元素对上一层每个元素的权向量 W
(1)构造下一层每个元素对上一层每个元素的成对比较矩阵;
(2)计算出成对比较矩阵的特征向量;
(3)由特征向量求出最大特征根λ max ;
(4)用最大特征根λ max 由公式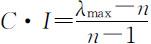 及
及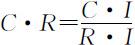 对成对比较矩阵进行一致性检验并通过.
对成对比较矩阵进行一致性检验并通过.
2.构建排序权向量表
把下层每个元素对上层每个元素的权向量按列排成表6.3所示表格形式:例如,假定:上层A 有m 个元素,A 1 ,A 2 ,…,Am ,且其层次总排序权向量为a 1 ,a 2 ,…,am ;下层B 有n 个元素B 1 ,B 2 ,…,Bn ,则按Bj 对Ai 个元素的单排序权向量的列向量为bij ,即如表6.3所示.
