表5.8　三种模型的比较

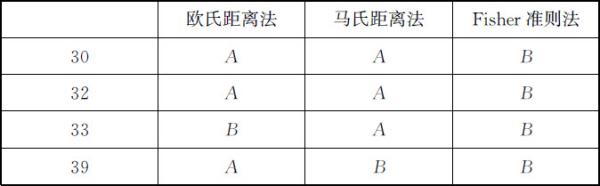
5.4　聚类分析

聚类分析是研究物以类聚的一个方法．分类问题在科学研究、生产实践、社会生活中到处存在．人们可以凭经验和专业知识实现分类，但当反映事物的性质、特性的指标较多，且对分类要求较高时，光凭经验和专业知识不能达到确切的分类目的，于是数学方法就被引进到分类问题中来．

在用聚类分析解决实际问题时，我们总把每个分类对象称为样品，并根据对象的性质和分类的目的选定若干指标（变量），对每一个样本测出所有的指标量，将得到的结果列成一个数据矩阵，这个样本资料矩阵就是聚类分析的出发点．从形式上看，这与相关分析、判别分析的出发点是一样的，这一点体现了多元统计方法的共性，但和多元分析的其他方法相比，聚类分析的方法是很粗糙的，且没有形成合适的模型，不论是聚类统计量还是聚类方法都没定型，理论也不完善．不过由于聚类分析方法能广泛应用于实际问题，在许多领域内不乏成功的范例．因此它和相关分析、判别分析一起被称为多元分析的三大分析．

需要指出的是，聚类分析和上节讨论的判别分析同是研究分类问题，但聚类分析一般是在不知类型的个数或对各种类型的结构未作任何假设情况下寻找处理客观分类的方法，而判别分析是在分类已知条件下寻找客观分类的依据，以此对新的不知所属的对象进行判别．

设所考察的对象有p 项指标，今有n 个样本，测得样本资料阵为：

其中x_ik 表示第i 个样品的第k 个指标值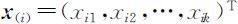． 表示第i 个样品观测值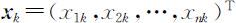， 则表示第k 个指标的n 次观测值．

一般的指标可分为如下的三类：

（1）间隔尺度　如人的身高、体重；零件的长度、直径；元件的电阻等，即指标可以用连续的数值表示．

（2）有序尺度　如酒可分为好、中、差三等；考核等级可分为为优、良、及格、不及格四级，即指标只可以用有序的等级号来描述，而没有明确数量表示．

（3）名义尺度　如业余爱好的体育、音乐、诗画等；人的职业有工人、农民、教师等，即指标既不能用数量表示，也没有次序关系．

对于不同类型的指标，应该用不同的处理方法来进行分类．下面介绍的聚类统计量、聚类方法都是针对间隔的尺度指标的．

1．样品间的距离

距离是一种聚类统计量，距离近的样品归为一类，而距离远的样品则应属于不同的类．

样品间最常用的距离是

（1）绝对值距离

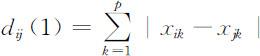
（2）欧氏距离

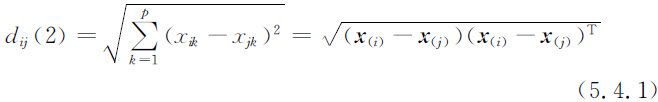
（3）闵可夫基斯（Minkowski）距离

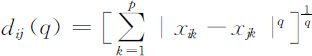
（4）马氏距离

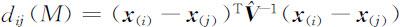
其中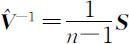 ，而 S 为样本离差阵，即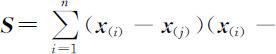 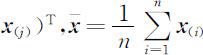．注意，当p 个指标之间数值差异太大时，直接使用以上各式计算距离常使数值较小的指标失去作用，这显然是很不合适的，为此需作标准化处理，即令

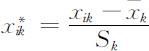
其中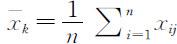 ，即n 个样品的第k 个指标的平均值， ．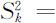

2．样品的相似系数

相似系数也是一种聚类统计量，它表示两样品之间的相似程度．因此，相似系数绝对值大的样品应归于一类，相似系数绝对值小的样品应属于不同的类．

常用的相似系数有以下三种：

（1）夹角余弦

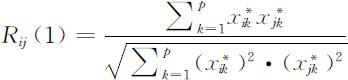
（2）相关系数

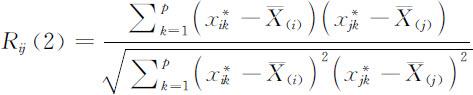
其中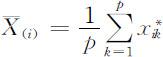 ，即第i 个样品的各标准化指标值的平均值．

（3）指数相似系数

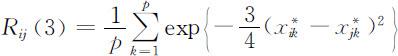
容易看出， ．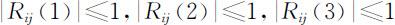

3．类与类之间的距离

设X ＝｛ x _（1） ， x _（2） ，…， x _{（n ）} ｝是样品集，G ₁ ，G ₂ ，…，G_m 是X 的非空子集，且满足条件

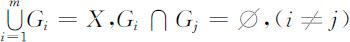
则称G ₁ ，G ₂ ，…，G_m 是X 的一个分类．

以下总用D （r，s ）表示类G_r 和G_s 之间的距离．又设G_r 、G_s 中样品个数分别记为n_r 、n_s ，以d_ij 表示类G_r 中第i 个样品与类G_s 中第j 个样品之间的距离，以i ∈G_r 表示样品X _{（i ）} 是G_r 中的一员．

记D （r，s ）表示类G_r 和G_s 之间的距离，G _r ，G_s 中样品个数分别记为n_r ，n_s ，以d_ij 表示类G_r 中第i 个样品与类G_s 中第j 个样品之间的距离，以i ∈G_r 表示样品 x _{（i ）} 是G_r 中的一员．

类与类之间的距离有多种定义法，常用的有以下四种：

（1） ．

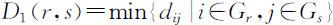称为类G_r 与G_s 之间的最短距离．

（2）

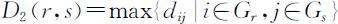
称为类G_r 与G_s 之间的最长距离．

（3）

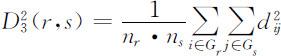
称为类G_r 与G_s 之间的类平均距离．

（4）

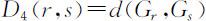
称为类G_r 与G_s 之间的类重心距离，其中d （G_r ，G_s ）表示类G_r 与G_s 的重心之间的距离．