3.3　线性规划建模方法基础

建立优化模型要确定实际中的优化问题通常有多个决策变量，用x 表示决策变量，f （x ）表示目标函数．实际问题一般对决策变量x 的取值范围有限制，不妨记作x ∈Ω，Ω 称为可行域．优化问题的数学模型可表示为：

Min（或Max）f （x ），x ∈Ω

当x 为1维或2维变量时，就是上节讨论的简单优化模型．

实际中的优化问题通常有多个决策变量，用n维向量 x ＝（x ₁ ，x ₂ ，…，x_n ）^T 表示，目标函数f （x ）是多元函数，可行域Ω 比较复杂，常用一组不等式（也可以有等式）g_i （x ）⩽0（i ＝1，2，…，m ）来界定，称为约束条件．一般地，这类模型可以表述成如下形式：

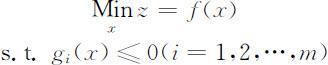
这里的s．t．（subject to）是“受约束于”的意思．

显然，上述模型属于多元函数的条件极值问题的范围，然而许多实际问题归结出的这种形式的优化模型，其决策变量个数n 和约束条件的个数m 一般较大，并且最优解往往在可行域的边界上取得，这样就不能简单地用微分法求解．数学规划是解决这类问题的有效方法．

许多实际问题，如生产计划这样的经济管理领域的问题，其数学模型大多是线性规划．线性规划有哪些特征？实际问题具有什么性质，其模型才是线性规划？

①比例性

每个决策变量对目标函数的“贡献”，与该决策变量的取值成正比；每个决策变量对每个约束条件右端项的“贡献”，与该决策变量的取值成正比．

②可加性

各个决策变量对目标函数的“贡献”，与其他决策变量的取值无关；各个决策变量对每个约束条件右端项的“贡献”，与其他决策变量的取值无关．

③连续性

每个决策变量的取值是连续的．

比例性和可加性保证了目标函数和约束条件对于决策变量的线性性，连续性则允许得到决策变量的实数最优解．

一般地，线性规划模型可归结为如下形式：

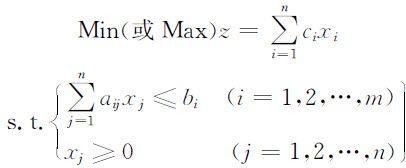
上述模型也可以表示为矩阵形式：

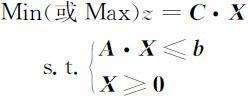
由此，可以定义线性规划模型的标准形为：

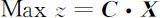
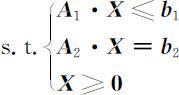
对于非标准形的线性规划模型都可以化为标准形，其方法如下：

（1）目标函数为最小化问题；即要求“Minz ”，可以换成“Max（-z ）＝- C·X ”．

（2）约束条件中的不等号问题；若约束条件中要求的是“ A ₁ · X ⩾ b ₁ ”，可换成“- A ₁ · X ⩽- b ₁ ”

可以利用数学工具Matlab软件、Lindo软件或者Lingo软件编程实现模型的求解．下面举一个例子．