图7.6　多层感知器结构示意图

多层感知器只允许一层连接权可调，这是因为无法给出一个有效的多层感知器学习算法．直到Rumelhart等人提出了BP算法之后，才真正实现了多层感知器的设想．

②BP算法

BP算法仍然是一种监督学习算法，它由两个阶段组成：逐层状态更新的正向传播阶段和误差的反向传播阶段．在正向传播阶段，给定的模式从输入层单元传到隐层单元，隐层单元处理后将输出传给下一层，这种状态的更新逐层向后传播，每一层神经元的状态只影响下一层神经元的状态，最终到达输出层，如果输出层得不到期望的输出结果，则进入误差反向传播阶段．在误差反向传播阶段，误差信号沿原来的连接通路返回，网络根据反向传播的误差信号修改各层之间的连接权，使误差信号达到最小．

BP算法的学习是对简单的δ 学习规则的推广和发展，其输出单元与隐层单元的误差计算是不同的．下面详细介绍采用BP算法的学习过程．

由图7.6可知，输入层中任一神经元的输入等于输入模式向量的相应分量，对其余各层，设某层的任一神经元j 的输入为net_j ，输出为y_j ，与j 相邻的低一层（靠输入层方向）中任一神经元i 的输出为y_i ，则有：

式中，ω_ij 为神经元i 与神经元j 之间的连接权；f （net_j ）为神经元的输出函数，这里取S型函数，为：

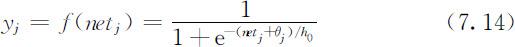
式中，θ_j 为神经元的阈值，它影响输出函数水平方向的位置；h ₀ 是用来修改输出函数形状的参数，输出函数如图7.7所示．设输出层中第k 个神经元的实际输出为y_k ，输入为net_k ，与输出层相邻的隐层中任一神经元j 的输出为y_j ，则y_k 和net_k 分别为：

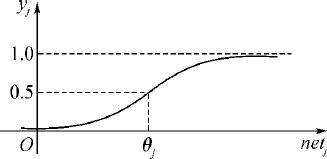
图7.7　输出函数f （net_j ）

对于一个输入模式X_p ，若输出层中第k 个神经元的期望输出为d_pk ，实际输出为y_pk ，则输出层的输出方差为：

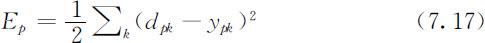
若输入N 个模式，则网络的系统均方差为：

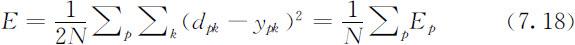
权值ω_jk 的修改应使E或E_p 最小，因此ω_jk 应沿E_p 的负梯度方向变化．也就是说，当输入X_p 时，ω_jk 的修正增量Δ_p ω_jk 应与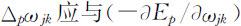 成正比，即：

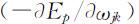又可以写为：

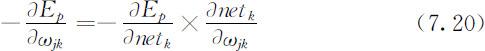
由式（7.15）得到：

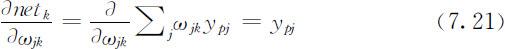
令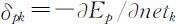 ，经推导得输出单元的误差和修正增量为

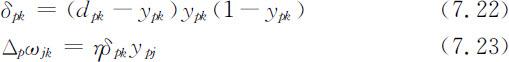
对于与输出层相邻的隐层中的神经元j 和比该隐层低一层中的神经元i ，可算得误差和修正增量为

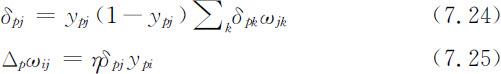
式如（7.22）和式（7.24）所示，输出层中神经元输出的误差反向传播到前面各层，对各层之间的权值进行修正．

③BP算法的具体步骤

Step1：对权值和神经元阈值初始化．给所有权值和阈值赋以在（0，1）上分布的随机数．

Step2：输入样本，指定输出层各神经元的希望输出值d ₁ ，d ₂ ，…，d_M ．

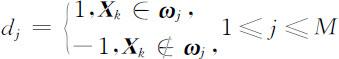
式中，d_j 为第j 个神经元的期望输出；ω_j 表示第j 个模式类．

Step3：依次计算每层神经元的实际输出，直到计算出输出层各神经元的实际输出y ₁ ，y ₂ ，…，y_M ．各神经元的输出根据式（7.14）进行计算．

Step4：修正每个权值．从输出层开始，逐层向低层递推，直到第一隐层．递推公式如下：

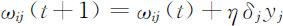
式中，ω_ij （t ）是t 时刻从神经元i （输入层或隐层神经元）到高一层神经j （隐层或输出神经元）的连接权；y_i 是神经元i 在t 时刻的输出．η 是步长调整因子，0<η <1．如果神经元j 是输出层的一个神经元，则：

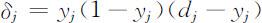
如果神经元j 是隐层的一个神经元，则：

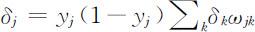
式中，y_j 是神经元j 在t 时刻的输出，k 是神经元j 的上一层（靠输出层方向）神经元的编号．如果权值按下面的方式修正，收敛可能更快，且权值会平滑地变化

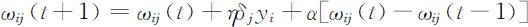
式中，α 是平滑因子，0<α <1．若把神经元的阈值当成一个权值，相应的输入模式增加一个分量1，则可以用调整权值的方法调整阈值．

Step5：转到第二步．如此循环，直到权值稳定为止．

BP算法是一个很有用的算法，因此受到广泛重视，但也存在一些问题，主要是存在局部极小值问题；算法收敛速度很慢；如何选取隐层单元的数目尚无一般性指导原则；新加入的学习样本会影响已学完样本的学习结果等．

对于隐层数目的问题，Lippman做了简单的论证．可以证明，包含两个隐层的多层感知器能形成任意复杂的判决界面．第一个隐层形成一些超平面，第二个隐层形成一些判决区，并根据第一个隐层形成的超平面进行“与”运算，输出层进行“或”运算．即使同类模式处于模式空间几个不连通的区域中，这种网络也能进行正确的判决．一般说来，隐层越多，网络的学习能力越强．有研究发现，若隐层单元的数目以指数规律增加，则学习异或问题的速度线性增加；另一些研究发现，在某些问题中学习速度会随着隐层数目的增加而减少．

7.2.5　BP神经网络Matlab程序举例

例1　对两个输入一个输出的神经网络学习

％创建一个新的前向神经网络

％函数newff建立一个可训练的前馈网络．这需要4个输入参数．

％第一个参数是一个R×2的矩阵以定义R个输入向量的最小值和最大值．

％第二个参数是一个设定每层神经元个数的数组．

％第三个参数是包含每层用到的传递函数名称的细胞数组．tansig和logsig统称Sigmoid函数，logsig是单极性S函数，tansig是双极性S函数，也叫双曲正切函数，pureln是线性函数，是结点的传输函数．

％最后一个参数是用到的训练函数的名称．traingdm是带动量的梯度下降法，trainlm是指L-M优化算法，trainscg是指量化共轭梯度法，除此之外还有traingdx、traingda、traingd等，都是权值的训练算法．

net.trainParam.epochs＝500；％设置训练参数，最多训练步数

net.trainParam.goal＝1e-6；％设置训练参数，误差性能目标值

net.trainParam.show＝50；％设置训练参数，系统每50步显示一次训练误差的变化曲线

net.trainParam.lr＝0.05；％设置训练参数，学习速率0.05

［net tr］＝train（net，P，T）；

％格式：train（net，P，T，Pi，Ai，VV，TV）

其中net为所建网络，P为网络输入，T为目标值，Pi为初始输入延迟，Ai为初始网络层延迟，VV为验证向量结构，TV为测试网络结构．

％返回值：net训练之后的网络，tr训练记录，Y网络输出，E网络误差，Pf最终输入延迟；％Af最终网络层延迟

A＝sim（net，P）；％A网络输出，T目标输出

例2　对单输入单输出的神经网络学习

close all

clear all

clc

P＝［-1∶0.05∶1］；％P为输入矢量

T＝sin（2piP）＋0.1*randn（size（P））；％T为目标矢量P在正弦曲线的附近取点

net＝newff（minmax（P），［20，1］，｛′tansig′，′purelin′｝）；％创建一个新的前向神经网络

net.trainFcn ＝′trainlm′；％采用L-M优化算法TRAINLM

net.trainParam.epochs＝500；％设置训练参数

net.trainParam.goal＝1e-6；％设置训练参数

net＝init（net）；％重新初始化

［net，tr］＝train（net，P，T）；％调用相应算法训练BP网络

A＝sim（net，P）；

E＝T-A；％计算仿真误差

MSE＝mse（E）％绘制匹配结果曲线

figure

plot（P，A，′o′，P，T，′＋′，P，sin（2piP），′：′）；

legend（′网络输出′，′目标值-带噪声′，′目标值-不带噪声′）