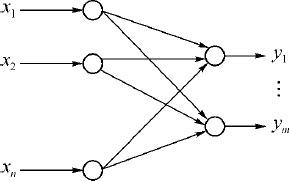
图7.4　Hebb学习规划示意图

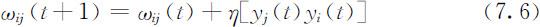
因为x_i （t ）＝y_i （t ）．（7.6）式可写成：

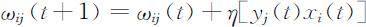
Hebb学习规则已经得到神经细胞学说的证实，由于具有一定的生物学依据，其思想很容易被接受，因此得到了较广泛的应用．

（2）δ 学习规则

误差修正学习方法是神经网络学习中另一类更重要的方法．最基本的误差修正学习方法，即常说的δ 学习规则描述如下：

Step1：选择一组初始权值ω_ij （1）；

Step2：计算某一输入模式对应的实际输出与期望输出的误差；

Step3：更新权值，阈值可视为输入恒为-1的一个权值：

式中，η 为学习因子，d_j ，y_j （t ）分别表示第j 个神经元的期望输出与实际输出；x_i （t ）为第j 个神经元的第i 个输入；

Step4：返回第（Step2）步，知道对所有的训练模式，网络输出均能满足要求．

生理学和解剖学的研究已表明，在动物学习过程中神经网络的结构修正即拓扑变化起着重要的作用．这意味着神经网络的学习不仅体现在权值的变化，而且在网络结构上已有变化．人工神经网络中关于结构变化的学习方法与权值修正方法并不完全脱离，两者具有补充作用．

7.2.3　神经网络的结构分类

神经网络按照结构、学习方式、功能等的不同有不同的分类，从连接结构上可以分为两大类：分层结构与相互连接结构．分层结构网络有明显的层次，信息的流向由输入层到输出层，构成一大类网络，即前馈网络．而相互连接结构的网络没有明显的层次，任意两个神经元之间都是可达的，具有输出单元到隐层单元或输入单元的反馈连接，这就形成了另一类网络，即反馈网络．

7.2.4　前馈神经网络

（1）感知器

感知器（perceptron）是F．Rosenblatt于1957年提出的一种神经网络模型．早期的研究人员试图用感知器模拟人脑的感知特征，但后来发现感知器的学习能力有很大的局限性，以致人们曾经对它的能力和应用前景得出了十分悲观的结论．尽管如此，这种神经网络模型的出现对早期神经网络的研究以及对后来许多神经网络模型的出现都产生了极大的影响．感知器的结构如图7.5所示．