3.4　线性规划方法建模案例分析

例1　加工奶制品的生产计划

1．问题

一奶制品加工厂用牛奶生产A ₁ ，A ₂ 两种奶制品，1桶牛奶可以在甲类设备上用12小时加工成3公斤A ₁ ，或者在乙类设备上用8小时加工成4公斤A ₂ ．根据市场需求，生产的A ₁ ，A ₂ 全部能售出，且每公斤A ₁ 获利24元，每公斤A ₂ 获利16元．现在加工厂每天能得到50桶牛奶的供应，每天正式工人的劳动时间为480小时，并且甲类设备每天至多能加工成100公斤A ₁ ，乙类设备的加工能力没有限制．试为该厂制订一个生产计划，使每天的获利最大，并进一步讨论一下3个附加问题：

①若用35元可以买到1桶牛奶，是否应作这项投资？若投资，每天最多购买多少桶牛奶？

②若可以聘用临时工人以增加劳动时间，付给临时工人的工资最多是每小时几元？

③由于市场需求变化，每公斤A ₁ 的获利增加到30元，是否应改变生产计划？

2．问题分析

这个优化问题的目标是使每天的获利最大，要做的决策是生产计划，即每天用多少桶牛奶生产A ₁ ，用多少桶牛奶生产A ₂ （也可以是每天生产多少公斤A ₁ ，多少公斤A ₂ ），决策受到3个条件的限制：原料（牛奶）供应、劳动时间、甲类设备的加工能力．按照题目所给，将决策变量、目标函数和约束条件用数学符号及式子表示出来，就可以得到如下的模型．

3．基本模型

（1）决策变量：设每天用x ₁ 桶牛奶生产A ₁ ；用x ₂ 桶牛奶生产A ₂ ．

（2）目标函数：设每天获利为z ．x ₁ 桶牛奶生产3x ₁ 公斤A ₁ ，获利24×3x ₁ ，x ₂ 桶牛奶生产4x ₂ 公斤A ₂ ，获利16×4x ₂ ，故z ＝72x ₁ ＋64x ₂ ．

（3）约束条件

原料供应生产A ₁ ，A ₂ 的原料（牛奶）总量不得超过每天的供应，即x ₁ ＋x ₂ ⩽50桶．

劳动时间　生产A ₁ ，A ₂ 的总加工时间不得超过每天正式工人总的劳动时间，即12x ₁ ＋8x ₂ ⩽480小时．

设备能力　A ₁ 的产量不得超过甲类设备每天的加工能力，即3x ₁ ⩽100．

非负约束　x ₁ 和x ₂ 均不能为负值，即x ₁ ⩾0和x ₂ ⩾0．

线性模型为：

4．模型求解

可以采用图解法和软件实现．这里介绍一下软件实现．用Lindo软件可以很方便地实现．在Lindo下打开一个新文件，像书写模型（3.4.1）～（3.4.5）一样，直接输入：

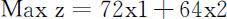
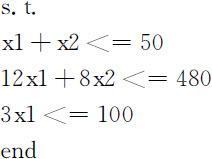
若做灵敏度分析，则有如下结果：

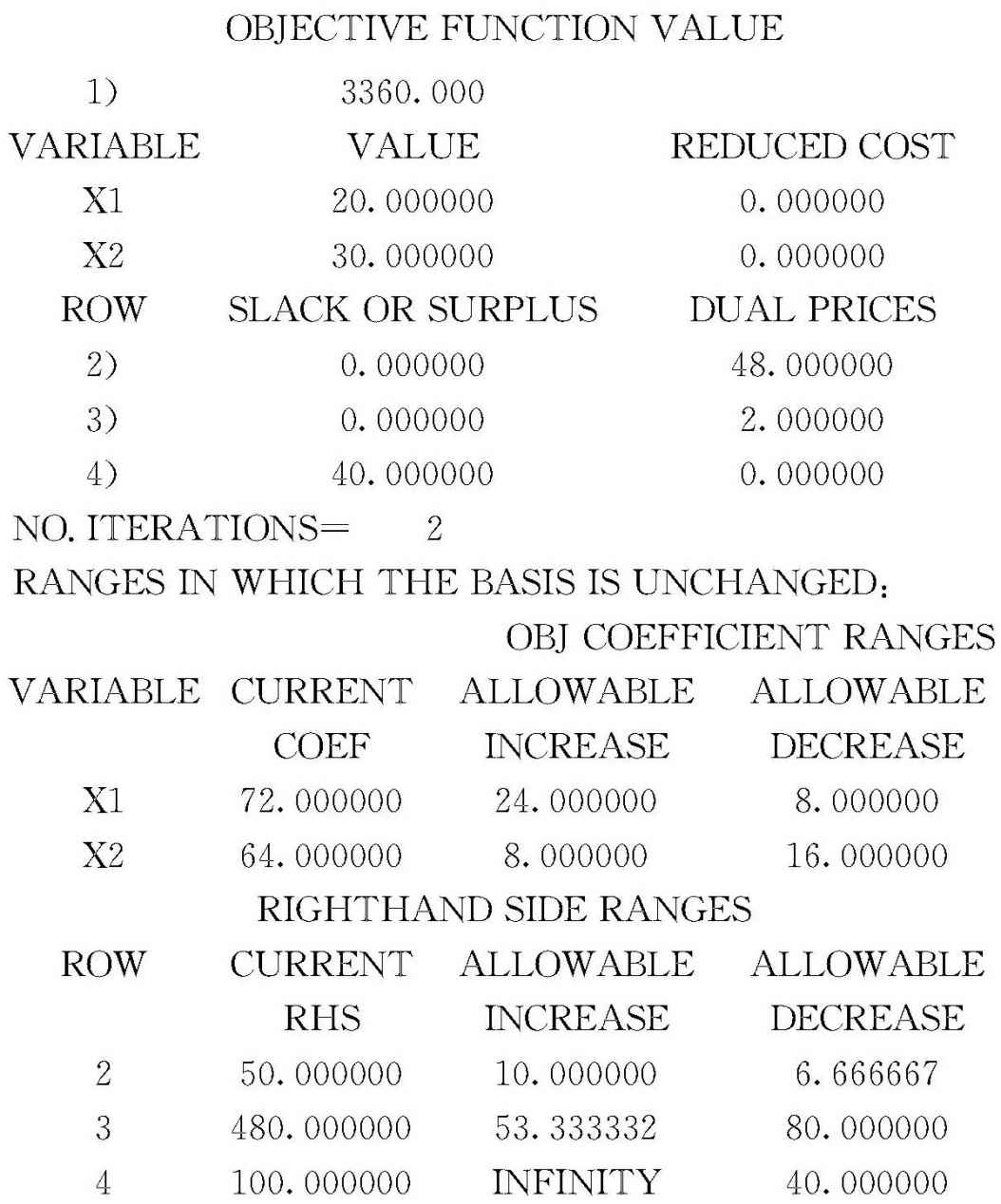
上述结果表明：当x ₁ ＝20，x ₂ ＝30时模型取得最优解z ＝3360．即用20桶牛奶生产A ₁ ，30桶牛奶生产A ₂ ，可获最大利润3360元．

5．结果分析

上面的输出中除了告诉我们问题的最优解和最优值以外，还有许多对分析结果有用的信息．

（1）3个约束条件的右端不妨看作3种“资源”：原料、劳动时间、甲类设备的加工能力．输出中的“SLACK OR SURPLUS”项给出这3种资源在最优解下是否有剩余；原料；2）和劳动时间；3）的剩余均为0，甲类设备的加工能力；4）尚有40公斤剩余．这表明：原料和劳动时间已用完，而甲类设备的能力有余．一般称“资源”剩余为0的约束为紧约束（或有效约束）．

（2）目标函数可以看作“效益”，成为紧约束的“资源”一旦增加，“效益”必然跟着增长．输出中的“DUAL PRICES”项给出这3种资源在最优解下“资源”增加一个单位时“效益”的增量．原料2）增加1个单位（1小时）时利润增长2元，而增加非紧约束甲类设备的生产能力时显然不会使利润增加．这里，“效益”的增量可以看作“资源”的潜在价值，经济学上称为“影子价格”，即1桶牛奶的影子价格为48元，1小时劳动的影子价格为2元，甲类设备的影子价格为0．

读者可以用直接求解的办法验证上面的结论，即将输入文件中原料约束2）右端的50改为51，会发现得到的最优值（利润）恰好增长48元．

用影子价格的概念很容易回答附加问题①：用35元可以买入1桶牛奶，低于1桶牛奶的影子价格，当然应该做这项投资．回答附加问题②：聘用临时工人以增加劳动时间，付给的工资低于劳动时间的影子价格才可以增加利润，所以工资最多是每小时2元．

（3）目标函数的系数发生变化时（假定约束条件不变），最优解和最优值会改变吗？上面输出的目标系数变化范围“OBJ COEFFICIENT RANGES”项中的“ALLOWABLE INCREASE”项和“ALLOWABLE DECREASE”项给出了最优解不变条件下目标函数系数的允许变化范围：x ₁ 的系数为：（72-8，72＋24）＝（64，96），x ₂ 的系数为：（48，72）．注意：x ₁ 系数的允许范围需要x ₂ 系数64不变，反之亦然．

用这个结果很容易回答附加问题③：若每公斤A ₁ 的获利增加到30元，则x ₁ 的系数变为30×3＝90，在允许范围内，所以不应改变生产计划．

（4）对“资源”的影子价格作进一步的分析.35元一桶的牛奶可以买入，可以买入无限桶牛奶吗？显然，他受到“资源”紧约束条件的限制，不可能无限制的买入．要买入多少桶牛奶能使得获利最大？上面输出的右端变化范围“RIGHTHAND SIDE RANGES”项中的“ALLOWABLE INCREASE”项和“ALLOWABLE DECREASE”项给出的是影子价格有意义条件下约束右端的限制范围：原料2）最多增加10桶牛奶，劳动时间最多增加53小时．

现在可以回答附加问题①的第2问：虽然应该批准用35元买1桶牛奶的投资，但每天最多购买10桶牛奶．也可以用低于每小时2元的工资聘用临时工人以增加劳动时间，但最多增加53小时．

评注：本例在产品利润、加工时间等参数均可设为常数的情况下，建立了线性规划模型．线性规划模型的三要素：决策变量、目标函数和约束条件．线性规划模型可以方便地用Lindo软件求解，得到内容丰富的输出，利用其中的影子价格和灵敏度分析（一般情况下Lindo给出的是充分条件），可对模型结果作进一步的研究，它们对实际问题常常是十分有益的．