3.5　整数规划建模方法案例分析

上节中，研究的对象都是连续可分的，于是决策变量是连续的，建立的模型是线性规划．本节中考虑研究对象是不可分的情形．

例2　汽车厂生产计划

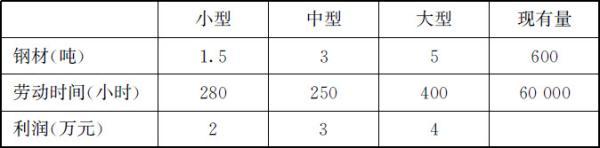
问题：一汽车厂生产小、中、大三种类型的汽车，已知各类型每辆汽车对钢材、劳动时间的需求，利润以及每月工厂钢材、劳动时间的现有量如下表所示．试制订月生产计划，使工厂的利润最大．

进一步讨论：由于各种条件限制，如果生产某一类型汽车，则至少要生产80辆，那么最优的生产计划应作何改变？

汽车厂的生产数据

（1）模型建立与求解

设每月生产小、中、大型汽车的数量分别为x ₁ ，x ₂ ，x ₃ ，工厂的月利润为z，问题中所给参数均不随生产数量变化的假设下，立即可得线性规划模型：

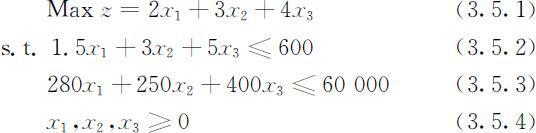
用Lindo求解，得到输出：

可以看到：最优解x ₁ ＝64.51629，x ₂ ＝167.741928，x ₃ ＝0，出现了小数，显然不合适．通常的解决办法有如下3种：

①简单地舍去小数，取x ₁ ＝64，x ₂ ＝167，它可能会接近最优的整数解，可算出相应的目标函数值z ＝629，与线性规划模型得到的最优解z ＝632.2581相差不大．

②在上面这个解的附近试探：如取x ₁ ＝65，x ₂ ＝167；x ₁ ＝64，x ₂ ＝168等．从输出可知：约束是紧的，所以若试探x ₁ ，x ₂ 大于线性模型最优解时，必须检验他们是否满足约束条件（3.5.2），（3.5.3）然后计算函数值z ，通过比较可能得到更优的解．

③在线性规划模型中增加约束条件：

这样得到的（3.5.1）～（3.5.5）式称为整数规划．整数规划可以用Lindo直接求解，输入以下语句即可：

其中“gin 3”是“3个变量均为整数”的说明语句．求解得到输出：

整数规划的最优解x ₁ ＝64，x ₂ ＝168，x ₃ ＝0，最优值z ＝632，即问题要求的月生产计划为生产小型车64辆，中型车168辆，不生产大型车．

对于问题中提出的“如果生产某一类型汽车，则至少要生产80辆”的限制，上面得到的整数规划的最优解不满足这个条件．这种类型的要求是实际生产中经常提出的．下面以本问题为例说明解决这类要求的办法．

原问题建立的线性模型（3.5.4）式修改为：

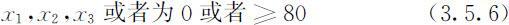
下面提供求解模型（3.5.1）～（3.5.3），（3.5.6）的2种线性规划方法：

①分解为多个线性规划模型

（3.5.6）式分解为以下8种情形：

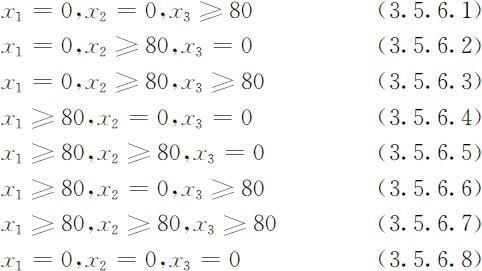
情形（3.5.6.8）显然不是方程的解．通过简单的判断，容易知道情形（3.5.6.3）和情形（3.5.6.7）不满足约束条件（3.5.2），也不可能是问题的解．对剩余的5种情形下分别求解，然后比较目标函数值，可知最优解在情形（3.5.6.5）得到：x ₁ ＝80，x ₂ ＝150.399994，x ₃ ＝0，z ＝611.2．最后，加上对x ₁ ，x ₂ ，x ₃ 的整数约束，在这个解的附近试探，可得x ₁ ＝80，x ₂ ＝150，x ₃ ＝0，最优解z ＝610．

当然，也可以不检查是否满足约束条件，解8种情形的线性规划模型，结果和上述结果一样．

②引入0-1变量，化为整数规划

设y ₁ 只取0，1两个值，则“x ₁ 或者为0或者⩾80”等价于：

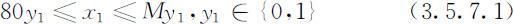
其中M 为相当大的正数，本例可取1000（x ₁ 不可能超过1000）．类似地有

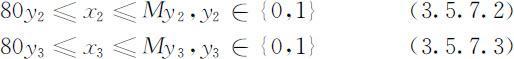
于是（3.5.1）～（3.5.3），（3.5.5），（3.5.7.1）～（3.5.7.3）构成了一个特殊的整数规划模型（既有一般的整数变量，又有0-1变量），用Lindo直接求解时，输入的最后要加上0-1变量的说明语句：

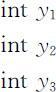
得到输出（只列出需要的结果）：

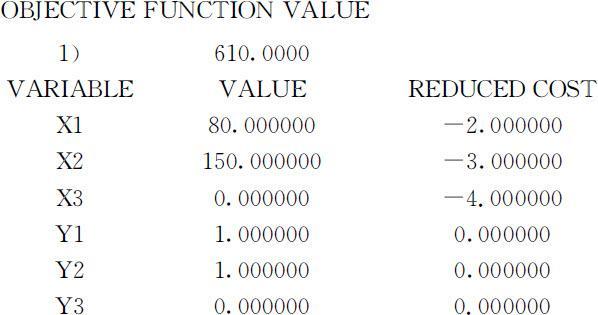
其结果和方法①结果相同．