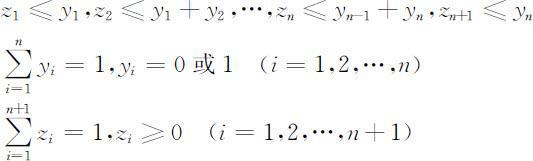3.6　非线性规划方法建模案例分析

上节中的例2中模型（3.5.1）～（3.5.3），（3.5.6）也可以化为非线性规划来求解．

条件（3.5.4），（3.5.6）可表示为

式子左端是决策变量的非线性函数，（3.5.1）～（3.5.3），（3.6.1）～（3.6.3）构成非线性规划．非线性规划虽然也可以用现成的数学软件求解（如Lingo或Matlab），但是其结果常依赖于初值的选择．实践说明，本例仅当初值非常接近上面方法算出的最优解时，才能得到正确的结果．

像汽车这样的对象自然是整数变量，应该建立整数规划模型，但是求解整数规划比线性规划要难得多（即使使用数学软件），所以当整数变量取值很大时，常作为连续变量用线性规划处理．

为了考虑（3.5.6）式这样的条件，通常是引入0-1量，建立整数规划模型，而一般尽量不用非线性规划．

下面介绍用Lingo软件求非线性规划模型的解的方法．

例3　原油采购与加工

某公司用两种原油（A 和B ）混合加工成两种汽油（甲和乙）．甲、乙两种汽油含原油A 的最低比例分别为50％和60％，每吨售价分别为4800元和5600元．该公司现有原油A 和B 的库存量分别为500吨和1000吨，还可以从市场上买到不超过1500吨的原油A ．原油A 的市场价为：购买量不超过500吨时的单价为10000元／吨；购买量超过500吨但不超过1000吨时，超过500吨的部分8000元／吨；购买量超过1000吨时，超过1000吨的部分6000元／吨．该公司应如何安排原油的采购和加工？

问题分析

安排原油采购、加工的目标只能是利润最大，题目中给出的是两种汽油的售价和原油A 的采购价，利润为销售汽油的收入与购买原油A 的支出之差．这里的难点在于原油A 的采购价与购买量的关系比较复杂，是分段函数关系，能否及如何用线性规划、整数规划模型加以处理是关键所在．

模型建立

设原油A 的购买量为x ，根据题目所给数据，采购的支出c （x ）可表示为如下的分段线性函数（以下价格以千元／吨为单位）：

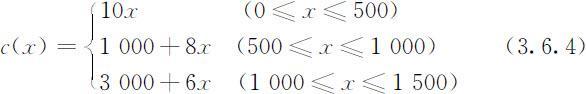
设原油A 用于生产甲、乙两种汽油的数量分别为x ₁₁ 和x ₁₂ ，原油B 用于生产甲、乙两种汽油的数量分别为x ₂₁ 和x ₂₂ ，则总的收入为4.8（x ₁₁ ＋x ₂₁ ）＋5.6（x ₁₂ ＋x ₂₂ ）．于是本例的目标函数（利润）为

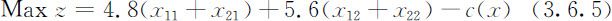
约束条件包括加工两种汽油用的原油A 、原油B 库存量的限制，和原油A 购买量的限制，以及两种汽油含原油A 的比例限制，它们表示为：

由于（3.6.4）式中的c （x ）不是线性函数，（3.6.4）～（3.6.11）给出的是一个非线性规划．而且，对于这样用分段函数定义的c （x ），一般的非线性规划软件也难以输入和求解．能不能想办法将该模型化简，从而用现成的软件求解呢？

模型求解

下面介绍三种求解方法：

（1）方法Ⅰ

一个自然的想法是将原油A 的采购量x 分解为三个量，即用x ₁ ，x ₂ ，x ₃ 分别表示以价格10千元／吨、8千元／吨、6千元／吨采购的原油A 的吨数，总支出为c （x ）＝10x ₁ ＋8x ₂ ＋6x ₃ ，且：

这里目标函数变为线性函数：

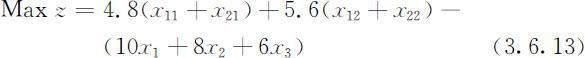
应该注意到，只有当以10千元／吨的价格购买x ₁ ＝500吨时，才能以8千元／吨的价格购买x ₂ （x ₂ >0），这个条件表示为

同理，只有当以8千元／吨的价格购买x ₂ ＝500吨时，才能以6千元／吨的价格购买x ₃ （x ₃ >0）

此外，x ₁ ，x ₂ ，x ₃ 的取值范围是

由于有非线性约束（3.6.14），（3.6.15），（3.6.6）～（3.6.15）构成非线性规划模型．将该模型输入Lingo软件如下：

运行程序得到如下的输出结果：

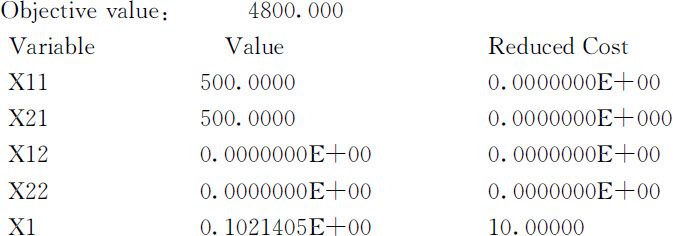
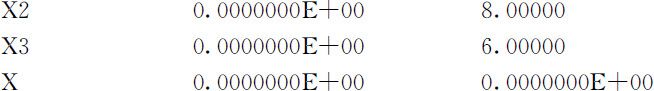
最优解是用库存的500吨原油A 、500吨原油B 生产1000吨汽油甲，不购买新的原油A ，利润为4800000元．

值得注意的是：Lingo得到的结果只是一个局部最优解，还能得到更好的解吗？

（2）方法Ⅱ

引入0-1变量将（3.6.14）和（3.6.15），转化为线性约束．

令y ₁ ＝1，y ₂ ＝1，y ₃ ＝1分别表示以10千元／吨、8千元／吨、6千元／吨的价格采购原油A ，则约束（3.6.14）和（3.6.15）可以替换为

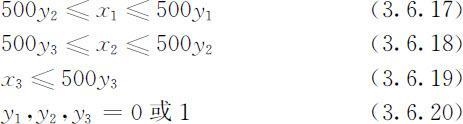
（3.6.6）～（3.6.13），（3.6.16）～（3.6.20）构成整数规划模型，利用Lindo软件求解，可得如下结果：

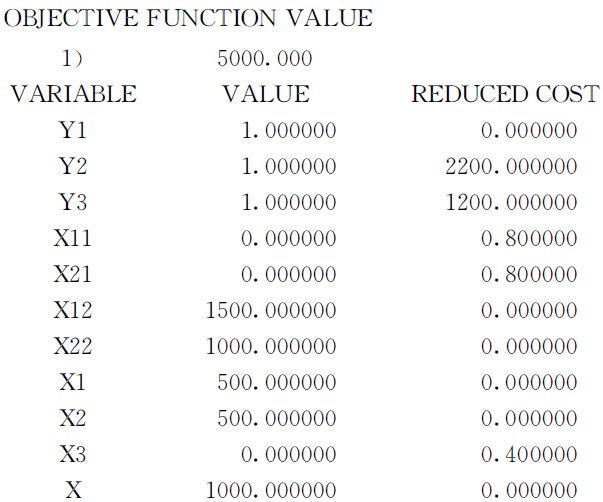
最优解中购买1000吨原油A ，与库存的500吨原油A 和1000吨原油B 一起，共生产2500吨汽油乙，利润为5000000元，高于非线性规划模型得到的结果．

（3）方法Ⅲ

直线处理分段线性函数c （x ）．（3.6.4）式表示的c （x ）图象如图3.3所示．

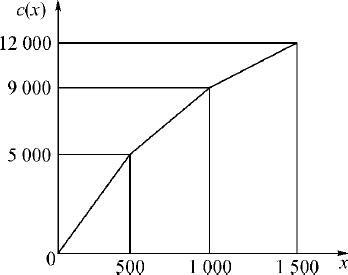
图3.3　分段线性函数c （x ）的图象

记x 轴上的分点为b ₁ ＝0，b ₂ ＝500，b ₃ ＝1000，b ₄ ＝1500．当x 在第1个小区间［b ₁ ，b ₂ ］时，记x ＝z ₁ b ₁ ＋z ₂ b ₂ ，z ₁ ＋z ₂ ＝1，z ₁ ，z ₂ ⩾0，因为c （x ）在［b ₁ ，b ₂ ］是线性的，所以c （x ）＝z ₁ c （b ₁ ）＋z ₂ c （b ₂ ）．同样，当x 在第2个小区间［b ₂ ，b ₃ ］时，记x ＝z ₂ b ₂ ＋z ₃ b ₃ ，z ₂ ＋z ₃ ＝1，z ₂ ，z ₃ ⩾0，c （x ）＝z ₂ c （b ₂ ）＋z ₃ c （b ₃ ）．当x 在第3个小区间［b ₃ ，b ₄ ］时，记x ＝z ₃ b ₃ ＋z₄ b ₄ ，z ₃ ＋z₄ ＝1，z ₃ ，z₄ ⩾0，c （x ）＝z ₃ c （b ₃ ）＋z₄ c （b ₄ ）．

为了表示x 在哪个小区间，引入0-1变量y_k （k ＝1，2，3），当x 在第i 个小区间时，y_k ＝1，否则y_k ＝0．这样，z_i （i ＝1，2，3，4），y_k （k ＝1，2，3）应该满足：

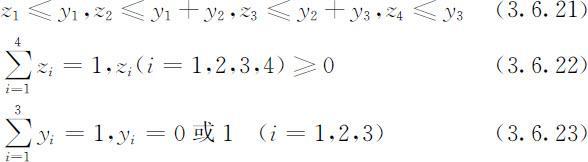
此时，x 和c （x ）统一表示为：

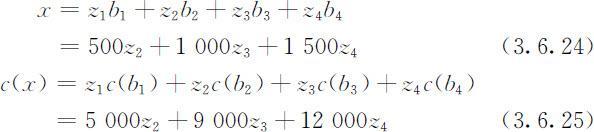
（3.6.5）～（3.6.11），（3.6.21）～（3.6.25）也构成一个整数规划模型，将它输入Lindo软件求解，得到的结果与方法Ⅱ相同．

这个问题的关键是处理分段线性函数，我们推荐化为整数规划模型的方法Ⅱ和方法Ⅲ，方法Ⅲ更具一般性，其做法如下：

设一个n 段线性函数f （x ）的分点为b ₁ ⩽…⩽b_n ⩽b _{n ＋1} ，引入z_k 将x 和f （x ）表示为

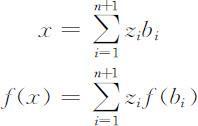
z_k 和0-1变量满足：