3.7　动态规划方法建模与案例分析

动态规划是一种将复杂的阶段决策问题转化为一系列比较简单的最优化问题的方法，它的基本特征是优化过程的多阶段性．

动态规划是求解某一类问题的一种方法，是考查问题的一种途径，而不是一种算法，它没有标准的数学表示式和具体的算法，必须具体问题具体分析．

动态规划是一种用于处理多阶段决策问题的数学方法，主要是先将一个复杂的问题分解成相互联系的若干阶段，每个阶段即为一个子问题，然后逐个解决，当每个阶段的决策确定之后，整个过程的决策也就确定了．阶段一般用时间段来表示（即与时间有关），这就是“动态”的含义，把这种处理问题的方法称为动态规划方法．

3.7.1　动态规划的基本概念和基本方法

1．动态规划的基本概念

（1）阶段和阶段变量：阶段是指一个问题需要作出决策的步骤，即把问题的过程分为若干个相互联系的阶段，使能按阶段的次序求解，描述阶段的变量称为阶段变量，常用k 表示．

（2）状态和状态变量：在多阶段决策过程中，每一阶段都具有一些特征（自然状况或客观条件），这就是状态，用来描述状态的变量称为状态变量．通常第k 阶段的状态变量用s_k （k ＝1，2，…，n ）表示，它的取值可以是一个数，一组数或一个向量等，状态变量可取值的全体所构成的集合称为可达状态集合（或允许状态集合），用S_k （k ＝1，2，…，n ）表示．

（3）决策和决策变量：当过程处于某一阶段的某个状态时，可以做出不同的决定（或选择），从而确定下一阶段的状态，这种决定称为决策，描述决策的变量称为决策变量，用x （s_k ）表示第k 阶段s_k （k ＝1，2，…，n ）状态的决策变量．决策变量的取值范围称为允许决策集合，用D_k （s_k ）表示第k 阶段状态s_k （k ＝1，2，…，n ）状态的决策变量集合，即x_k （s_k ）∈D_k （s_k ）（k ＝1，2，…，n ）．

（4）策略与子策略：一个按顺序排列的决策组成的集合称为策略．由第k 阶段开始到终止状态为止的过程，称为问题的后部子过程，或k 子过程．由k 子过程的每一阶段的决策按顺序排列组成的决策函数序列｛x_k （s_k ），…，x_n （s_n ）｝，称为k 子策略，记为P_k，n （s_k ），即

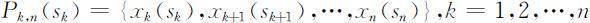
当k ＝1时，此决策函数序列称为全过程的一个策略，记为P _1，n （s ₁ ），即

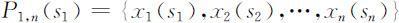
可供选择的策略范围称为允许策略集合，用P 表示，从允许策略集合中找出达到最优效果的策略称为最优策略．

（5）状态转移函数：状态转移函数是在确定多阶段决策过程中，由一个状态到另一个状态的演变过程．

如果给定了第k 阶段状态变量s_k 和该阶段的决策变量x_k （s_k ），则第k ＋1阶段的状态变量s _{k ＋1} 的值也随之而定，即s _{k ＋1} 随s_k 和x_k （s_k ）的变化而变化．这种对应关系记为s _{k ＋1} ＝T_k （s_k ，x_k （s_k ）），称为状态转移方程，T_k （s_k ，x_k ）称为状态转移函数．

（6）指标函数（回收函数）：在多阶段决策过程中，用来衡量所实现过程优劣的一种数量指标，称为指标函数，或回收函数．它是定义在全过程或所有子过程上的数量函数，即是各阶段的状态和决策变量的函数，记为V_k，n ，即

指标函数具有可分离性和递推关系：

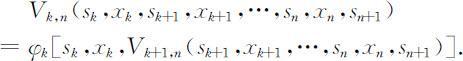
特别地，有两种常见的形式：

①全过程和任一子过程的指标函数是它所包含的各阶段指标函数的和，即

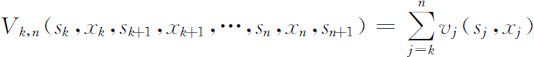
递推关系式为：

②全过程和任一子过程的指标函数是它所包含的各阶段指标函数的乘积，即

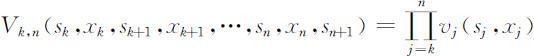
递推关系式为：

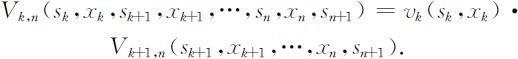
（7）最优值函数：从第k 阶段状态变量s_k 开始到第n 阶段的终止状态s _{n ＋1} 的过程，采取最优策略所得到的指标函数值，称为最优值函数，记为f_k （s_k ）（k ＝1，2，…，n ），即

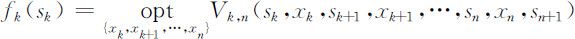
说明：在实际中，指标函数的含义可以是距离、利润、成本、时间、产品的产量、资源消耗等．

2．动态规划的基本条件

要对一个实际问题建立动态规划模型必须要满足下面的五个要素：

（1）问题可以转化为恰当的n 个阶段；

（2）正确选择状态变量s_k ，使它既能表达过程，又要具有无后效性和可知性；

①无后效性：如果某阶段状态已给定，则以后过程的发展不受以前各阶段状态的影响，也就是说当前状态就是未来过程的初始状态；

②可知性：规定的各阶段状态变量的值，由直接或间接地都是可以知道的．

（3）确定决策变量x_k 及每一阶段的允许决策集合D_k （s_k ）；

（4）写出状态转移方程：s_k ＝T_k （s_k ），k ＝1，2，…，n ；

（5）正确写出指标函数V_k，n 的关系，它满足下列性质：

①它是过程各阶段状态变量和决策变量的函数；

②具有可分离性和递推关系，即

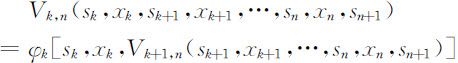
③函数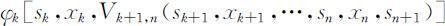 是关于V _{k ＋1，n} 严格单调的．

现在的问题是：对于动态规划的问题如何求解呢？

3．动态规划的基本方程

（1）逆序解法

设指标函数的形式为

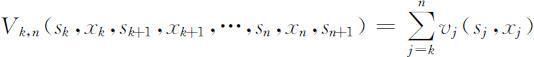
且具有上面的三条性质，则

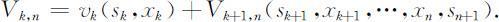
如果初始状态s_k 给定，则决策变量x_k （s_k ）随之确定，k 子过程的策略p_k，n （s_k ）也就确定，从而指标函数V_k，n 也同时确定了．于是，指标函数可以看成是初始状态和策略的函数，即对k 子过程的指标函数为V_k，n ［s_k ，p_k，n （s_k ）］，且有递推关系：

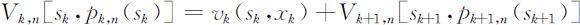
其中子策略为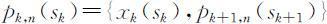 ，为决策变量x_k （s_k ）和子策略p _{k ＋1，n} （s _{k ＋1} ）的集合．

如果用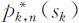 表示以第k 阶段状态s_k 为初始状态的后部子过程所有子策略中的最优子策略，则最优值函数为：

其中

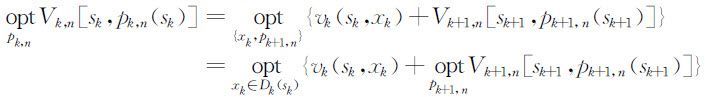
而

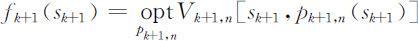
故：

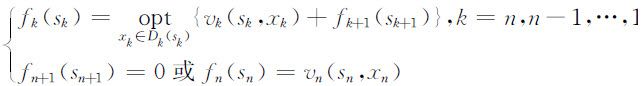
上式为动态规划逆序解法的基本方程．

求解时，由边界条件，从k ＝n 开始，由后向前逆推，逐段求最优决策和过程的最优值，最后求出f ₁ （s ₁ ）为问题的最优解．

（2）顺序解法

设过程的第k 阶段的状态为s_k ，其决策变量x_k 表示当状态处于s _{k ＋1} 的决策，即由x_k （s _{k ＋1} ）确定，则状态转移方程为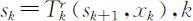 阶段的允许决策集合记为 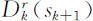，指标函数定义为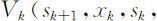 ，其最优值函数为：

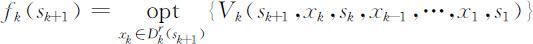
则

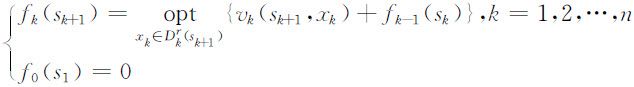
此为动态规划顺序解法的基本方程．

求解时，由边界条件，从k ＝1开始，由前向后顺推，逐段求出最优决策和过程的最优解，最后求出f_n （s _{n ＋1} ）为问题的最优解．

3.7.2　动态规划的求解方法

动态规划的求解方法有逆序解法和顺序解法两种．如果已知过程的初始状态s ₁ ，则用逆序解法；如果已知过程的终止状态s _{n ＋1} ，则用顺序解法．

1．逆序解法

设已知初始状态为s ₁ ，用f_k （s_k ）表示从第k 阶段初始状态s_k 到第n 阶段的最优值．

第n 阶段：指标函数的最优值记为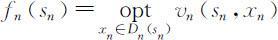 ，这是一维极值问题，不妨设有最优解x_n ＝x_n （s_n ），于是可有最优值f_n （s_n ）．

第n -1阶段：类似地有

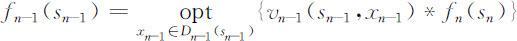
其中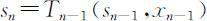 ，可解得最优解 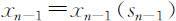，于是最优值为 ．

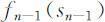不妨设第k ＋1阶段的最优解为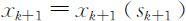： 和最优值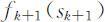 ，则对于第k 阶段有

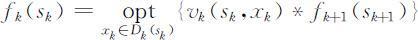
其中*表示“＋”或“×”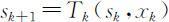， ，可解得最优解 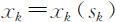和最优值为f_k （s_k ）．

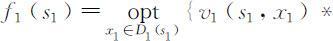
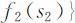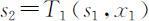依次类推，直到第1阶段，有 ，其中 ，可解得最优解x ₁ ＝x ₁ （s ₁ ）和最优值为f ₁ （s ₁ ）．

由于已知s ₁ ，则可知x ₁ 与f ₁ （s ₁ ）．从而可知s ₂ ，x ₂ ，f ₂ （s ₂ ），按上面的过程反推回去，即可得到每一阶段和全过程的最优决策．

2．顺序解法

设已知初始状态s _{n ＋1} ，用f_k （s _{k ＋1} ）表示从第1阶段初始状态s ₁ 到第k 阶段末的结束状态s _{n ＋1} 的最优值．

第一阶段：指标函数的最优值记为

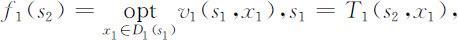
可解得最优解x ₁ ＝x ₁ （s ₂ ）和最优值f ₁ （s ₂ ）．

第二阶段：类似地有

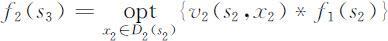
其中s ₂ ＝T ₂ （s ₃ ，x ₂ ），可解得最优解x ₂ ＝x ₂ （s ₃ ），于是最优值为f ₂ （s ₃ ）．

不妨设第k 阶段有

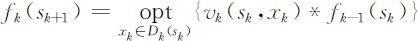
其中s_k ＝T_k （s _{k ＋1} ，x_k ），可解得最优解x_k ＝x_k （s _{k ＋1} ），于是最优值为f_k （s _{k ＋1} ）．

以此类推，直到第n 阶段有

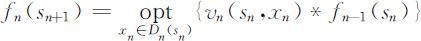
其中s_n ＝T_n （s _{n ＋1} ，x_n ），可解得最优解x_n ＝x_n （s _{n ＋1} ）和最优值f_n （s _{n ＋1} ）．

由于已知s _{n ＋1} ，则可知x_n 与f_n （s _{n ＋1} ）．从而可知s_n ，x _{n -1} ，f _{n -1} （s_n ），按上面的过程反推回去，直到s ₂ ，x ₁ ，f ₁ （s ₂ ），即得到整个过程和各阶段的最优决策．

3.7.3　动态规划方法的应用

1．一类静态规划的动态规划解法

所谓的静态规划是与时间概念无关的规划问题，例如：线性规划、目标规划、整数规划、非线性规划等．而动态规划是与时间概念有关的规划问题，动态规划的特点就是将问题按时间或空间特征而分成若干个阶段，从而将整个决策过程化为多阶段的决策问题．这也就是动态规划与静态规划的区别．对某些静态规划问题可以人为地引入时间因素，视为一个按阶段进行的动态规划问题，利用动态规划的方法求解．

在实际中，许多问题都具有形式上相同的数学模型，如载货问题、分配问题、背包问题等，其模型的一般形式为：

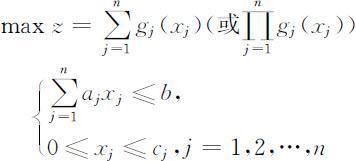
其中g_j （x_j ）为已知函数．当g_j （x_j ）均为线性函数时，则是线性规划；当g_j （x_j ）不全为线性函数时，则是非线性规划；当x_j 为整数时，则是整数规划．

一般解法：把问题分为n 个阶段，取x_k 为第k 阶段的决策变量，此时f _{n ＋1} （s _{n ＋1} ）＝0为边界条件，则问题的基本方程为

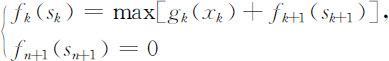
状态变量为 ；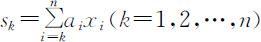

允许决策集合为 ；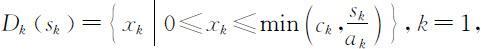

允许状态集合为 ；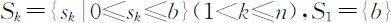

状态转移函数为 ．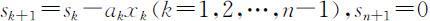

注：当决策变量x_k 要求取整数时，只要将允许决策集合限制在整数集合内取值即可．

2．资源分配问题的动态规划模型

设有某种资源总数量为a ，用于生产n 种产品，如果分配数量x_k 用于生产第k 种产品，其效益为g_k （x_k ），问如何分配资源使生产n 种产品的总效益最大？

此问题的静态模型为

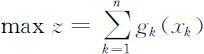
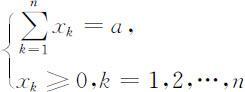
用动态规划方法求解，构造动态规划模型如下：

设状态变量s_k 表示分配用于生产第k 种产品至第n 种产品的资源数量，决策变量x_k 表示分配给生产第k 种产品的资源数量，状态转移方程为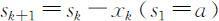 ，允许决策方程为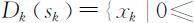 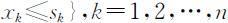．最优值函数f_k （s_k ）表示以s_k 数量的资源分配给第k 种产品至第n 种产品所得的最大效益，则问题的基本方程为

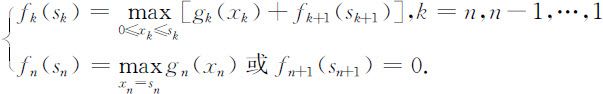
其最优值为f ₁ （a ）．

3．生产与存贮问题的动态规划模型

设某企业（公司）对某种产品要制订一项n 个阶段的生产（采购）计划．已知初始库存量为0，每阶段生产（或采购）的数量有上限为m ，每阶段的需求量已知为d_k （k ＝1，2，…，n ）（满足需要），且在第n 阶段结束时库存量为0．问如何制订每个阶段的生产（采购）计划使总的成本费用最小？

设x_k 为第k 阶段的生产量（或采购量），s_k 为第k 阶段结束时的库存量，则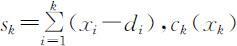 表示第k 阶段生产产品x_k 时的成本费用，包括准备成本K 和产品成本ax_k （a 为单位产品的成本），即

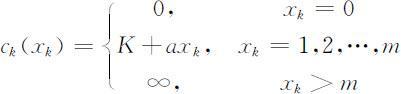
h_k （s_k ）表示k 阶段末库存量为s_k 所需的存贮费用，则k 阶段的费用为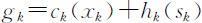 ，于是，问题的静态模型为

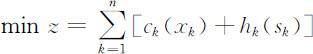
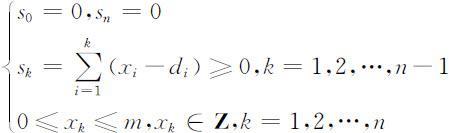
即为一整数非线性规划．

用动态规划方法求解，采用顺序解法：s_k 为状态变量，x_k 为决策变量，指标函数为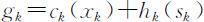 ，状态转移方程为 ，允许决策集合为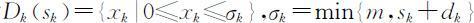 ，从第1阶段到第k 阶段末的最小费用为f_k （s_k ），则问题的基本方程为

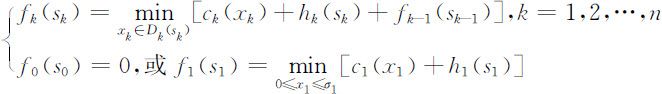
从边界条件出发，由基本方程可以算出每一阶段的f_k （s_k ），最后可得f_n （s_n ）＝f_n （0）为全过程的最优值，即最小费用．

4．背包问题的动态规划模型

设某人要装一个背包，可装物品的质量限度为a kg，共有n 种物品供选择（即编号为1，2，…，n ）．假设已知第k 种物品质量为w_k kg／件，携带x_k 件的使用价值为c_k （x_k ）（k ＝1，2，…，n ），问应如何选择物品（各多少件），使总的使用价值最大？

设x_k 为选择第k 种物品的件数，则问题的静态规划模型为

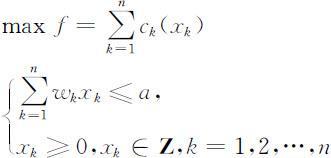
这是一个整数非线性规划问题．

问题的动态规划的模型：设将n 种物品分为n 个阶段，状态变量s_k 表示选择第1种至第k 种物品的总质量，即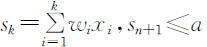 ，决策变量为x_k 表示选择第k 种物品的件数，则状态转移方程为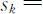 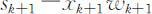，允许决策集合为 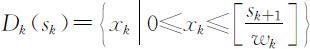，最优值函数f_k （s_k ）表示总质量不超过s_k kg时，选择第1种至第k 种物品的最大使用价值，即 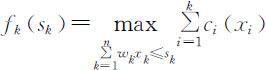．于是可得顺序解法的基本方程为

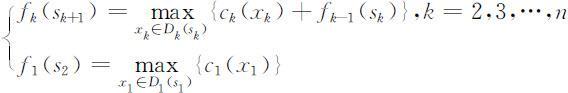
用顺序解法求解得各阶段的最优值函数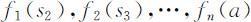 以及相应的决策函数 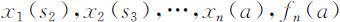为过程的最优值，反推回去可得到最优策略．

5．复合系统工作可靠性问题的动态规划模型

设由n 个部件组成的工作系统，只要有一个部件失灵，整个系统也就不能工作，为了提高系统的可靠性，在每个部件上均装有备用件，并可自动替换．实际上，备用件越多整个系统正常工作的可靠性越大，但系统的成本、质量、体积均相应增加，工作精度会相应降低．因此，现在的问题是在上述的条件之下，应如何选择各部件的备用件数，使整个系统的工作可靠性最大？

设第k 个部件装有x_k 个备件，正常工作的概率为p_k （x_k ），则整个系统正常工作的概率为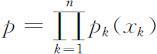 （衡量系统正常工作的可靠性的指标），装一个部件k 的备用件费用为c _k ，质量为w_k ，要求总费用不超过c ，总质量不超过w ，则问题的静态规划模型为

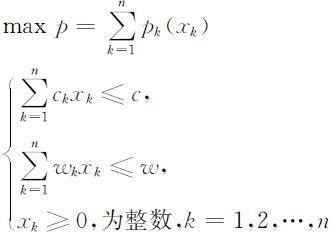
其问题可以转化为二维动态规划问题．两个状态变量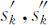 ：其中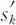， 表示由第k 个到第n 个部件所容许的总费用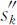， 表示由第k 个到第n 个部件所容许的总质量，决策变量x_k 为k 部件上装的备用件数，状态转移方程为

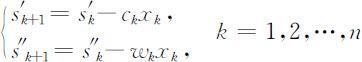
允许决策集合为：

最优值函数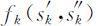 表示从k 部件到n 部件的最大可靠性，即：

于是可得问题的基本方程为：

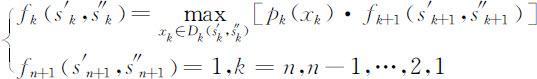
最后计算出f ₁ （c，w ）为系统的最大可靠性．