5.2　车辆安排模型算法

模型Ⅰ不考虑约束条件（3.8.10）就是一个整数规划问题，采用Lindo软件可以求得改变约束条件后得到的线性整数规划模型．为了使得模型的解满足约束条件（3.8.10），可以先进行铲位的初始布点，即按照一定的原则选定Ns 个铲位作为铲车的安置点，此时有ns ＝Ns ，然后对模型Ⅰ进行简化，去掉不必要的约束条件和变量，再用Lindo软件对简化后的模型求解．

①模型Ⅰ的优化算法

第1步：为铲车初始布点，布点方法是对模型（3.8.11）去除约束条件（3.8.6）、（3.8.9）和去掉变量整数约束，求线性规划的解X ，计算各铲位的能力利用率，按照利用率从高到低取Ns 个铲位作为初始点．

第2步：依据初始布点对模型进行简化，去掉没用的变量和精简约束条件．

第3步：对精简后的模型不含约束条件（3.8.9），含有约束条件（3.8.6）；采用Lindo软件求整数规划解．

第4步：利用得到的最优解求其他值．

②模型Ⅱ的求解算法

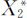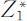第1步：采用模型Ⅰ的算法获得铲车布点并精简模型，得到模型的最优解5.2 车辆安排模型算法 - 图1 和目标函数值5.2 车辆安排模型算法 - 图2 ．

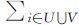
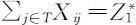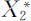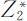第2步：对上一步的精简后的模型的约束条件添加约束5.2 车辆安排模型算法 - 图3 5.2 车辆安排模型算法 - 图4 作为从目标函数的约束条件，并求解得到模型的最优解5.2 车辆安排模型算法 - 图5 和目标函数值5.2 车辆安排模型算法 - 图6 ．

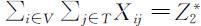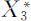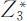第3步：对上一步模型的约束条件加入约束5.2 车辆安排模型算法 - 图7 作为从目标函数的约束条件，并求解得到模型的最优解5.2 车辆安排模型算法 - 图8 和目标函数值5.2 车辆安排模型算法 - 图9 ．

6．模型求解