5.1　方差分析

数据分析中所涉及的变量大致可以分为两大类，定量变量和定性变量．简单地说，定量变量就是它的取值可以量化，而定性变量的取值只能用语言或代号标明它的属性（如人的性别，病人病情的轻重，植物的品种等），有时，基于不同的数据分析目的，也可将定量变量转化为定性变量（如将职工的年收入划分为不同档次表示高收入、中等收入和低收入水平等）．当自变量均为定性变量时，称这种变量为因素．

方差分析是数理统计的基本方法之一．方差分析就是根据实验结果进行分析、推断各有关因素对试验结果的影响是否显著的方法．

为了方便，通常称试验结果为试验指标，试验中需要考察的可以控制的条件称为因素或因子，用A，B，C 表示，因素在试验中所处的不同状态称为水平，因素A 的a 个不同水平用A ₁ ，A ₂ ，…，A_a 表示．在一项试验中只有一个因素在改变称为单因素试验，处理单因素试验的统计推断方法叫单因素方差分析方法，处理多于一个因素的试验统计推断方法叫多因素方差分析方法．若在各水平下所做的试验次数都相同，则称为等重复试验，否则，称为不等重复试验．本节先简要介绍方差分析模型的建立方法，并以案例加以说明．

5.1.1　单因素方差分析模型

设所感兴趣的指标变量为Y ，影响Y 的因素为A ，它有a 个水平A ₁ ，A ₂ ，…，A_a ．在适当的试验设计下，在A 的各个水平上对Y 的取值进行独立观测，设在水平A ₁ 上对Y 独立观测了n_i 次，观测值为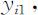 并假定其独立同分布于某个正态分布，这里i ＝1，2，…，a ，即不同水平上的各组观测值被认为是来自不同正态总体的一个样本（本章中，为避免在记号上过于复杂，我们不区分样本和它的观测值）．除因素A 可在其水平上变动外，尽可能控制试验的其他条件相同，即进一步可假定各总体具有相同的方差，因素A 的各水平的影响只体现在各总体均值的差异上．根据以上假定i ＝1，2，…，a ，有

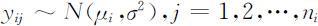
令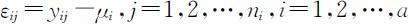 ，称ε_ij 为随机误差，则ε_ij ～N （0，σ ² ）且相互独立．这时单因素方差分析模型为

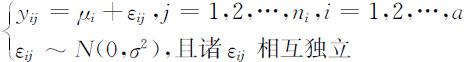
进一步令

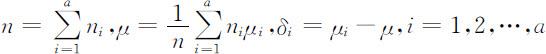
通常称μ 为总平均，δ_i 为水平A_i 的效应，δ_i 反映了因素A 的第i 个水平A_i 对Y 的影响的大小，且满足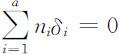 ．这时，单因素方差分析模型可进一步改写为

5.1.2　两因素等重复试验下的方差分析

设影响因变量Y 的因素有两个，分别记为A 和B ，其中因素A 有a 个不同水平A ₁ ，A ₂ ，…，A_a ，因素B 有b 个不同水平B ₁ ，B ₂ ，…，B_b ，在因素A 和B 的各水平组合下均做c （c >1）次试验，以y_ijk 记在水平组合（A_i ，B_j ）下第k 次试验的Y 的观测值．

于是，对于任意水平组合（A_i ，B_j ），假设（y _{ij 1} ，y _{ij 2} ，…，y_ijc ）为来自正态总体N （μ_ij ，σ ² ）的一个样本，即

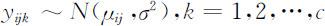
且各样本之间相互独立，令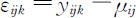 ，则两因素等重复试验下的方差分析模型可表示为：

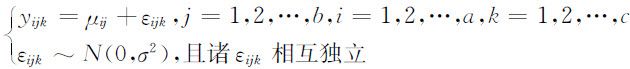
为进行统计分析，我们需要对水平组合（A_i ，B_j ）上的样本均值μ_ij 做进一步分解，为此引入如下记号：

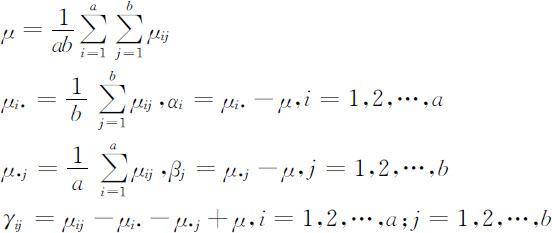
其中μ 称为总平均，α_i 为因素A 的水平A_i 的效应，β_j 为因素B 的水平B_j 的效应．为分析γ_ij 的意义，将其改为

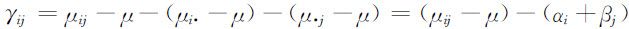
其中μ_ij -μ 反映了水平组合（A_i ，B_j ）对Y 的效应，在一般情况下，它并不等于水平A_i 的效应α_i 与水平B_j 的效应β_j 之和．我们将（A_i ，B_j ）的效应μ_ij -μ 减去A_i 的效应α_i 与B_j 的效应β_j 所得到的差γ_ij 称为A_i 与B_j 的交互效应，将全体γ_ij 称为A 与B 交互效应．在前述记号下，μ_ij 可分解为

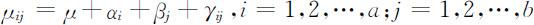
并且易证

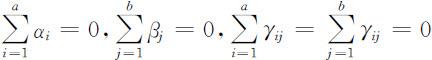
因此两因素等重复试验下的方差分析模型也可以等价地写为如下形式：

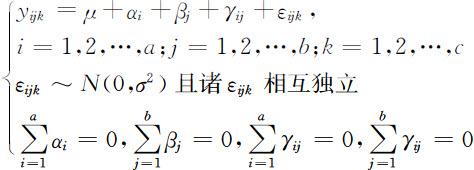
5.1.3　方差分析应用举例

例1　艾滋病疗效评价问题 （CUMCM2006年B题）

在艾滋病疗效评价问题中，要求就已有实验观察数据，对不同治疗方案以及用药时间进行评价．方差分析能用于判断控制变量的不同水平是否对观察变量产生显著影响．本问题共有三个控制变量：疗法、年龄和时间，属于多因素方差分析问题．

由原始数据，疗法分为4种，同时我们根据如下标准，把年龄分为4组，时间分为6组：

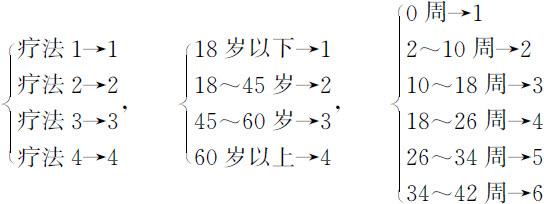
根据此问题的具体情况，共有三个控制变量：疗法、年龄和时间，再结合考虑疗法和时间的交互作用，建立模型如下：

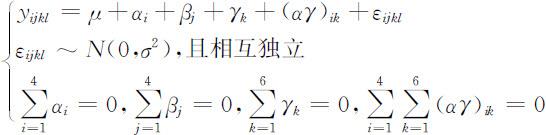
其中，α_i 表示第i 种疗法的效应，β_j 表示第j 个年龄段的效应，γ_k 表示第k 个测量时间段的效应，（αγ ） _ik 表示第i 种疗法与第k 个测量时间段的交互效应，ε_ijkl 表示试验误差．

利用SPSS统计分析软件进行多因素方差分析，得到方差分析表如表5.1所示．