7.1　遗传算法

7.1.1　基本概念

遗传算法（Genetic Algorithms，GA）是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法．它模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象，在每次迭代中都保留一组候选解，并按某种指标从解群中选取较优的个体，利用遗传算子（选择、交叉和变异）对这些个体进行组合，产生新一代的候选解群，重复此过程，直到满足某种收敛指标为止．

GA需要确定以下四个部分：

（1）编码（产生初始种群）

（2）适应度函数

（3）遗传算子（选择、交叉、变异）

（4）运行参数

7.1.2　编码

把实际问题表述为一种计算机能够识别并处理的某种方式称为编码，编码通过适应度函数来度量，因此一个编码就是问题的一组近似解．一个编码也称为一个个体，为了搜索到误差尽可能小的解，在开始时由计算机生成多个个体，称为初始种群．遗传算法就是对群体中的每一个体用适应度函数进行度量，找到具有较好适应度的个体，通过选择、交叉、变异等产生新一代，依此反复．从而找到问题的近似解．

常见的编码方式有：

（1）二进制编码：用一串0或1组合表达一个个体，如：00100011010，这是最常用的编码方式．个体的组成基本单位成为基因（Gene）．（这里每个0、1都是基因）

（2）互换编码：如旅行商问题中，一串基因编码用来表示遍历的城市顺序，如：234517986，表示九个城市中，先经过城市2，再经过城市3，依此类推．

（3）树形编码：一个个体表示为一棵树，这种编码又称为遗传规划（Genetic Programming）．

（4）值编码：每个个体是一串取值．这些取值可以是与问题有关任何值，如：整数，实数，字符或者其他．

7.1.3　适应度函数（fitness）

遗传算法对一个个体（解）的好坏用适应度函数值来评价，它的设计应结合求解问题本身的要求而定．适应度函数值越好（大或小），解的质量越好．适应度函数是遗传算法进化过程的驱动力，也是进行自然选择的标准，如TSP问题，234517986表示一种路径，遍历各城市路径之和越小越好，这样可以用这个路线的路径长度作为该问题的适应度函数，这时，长度越小适应度越好．

7.1.4　遗传算子（genetic operators）

A　遗传算子——选择（selection）

选择操作的任务就是按某种方法从父代群体中选取一些优秀的个体，遗传到下一代群体．

遗传算法使用选择运算来实现对群体中的个体进行优胜劣汰操作，即：适应度好的个体被遗传到下一代群体中的概率大；适应度低的个体，被遗传到下一代群体中的概率小．

SGA（基本遗传算法）中采用轮盘赌选择方法．轮盘赌选择又称比例选择算子，基本思想：各个个体被选中的概率与其适应度函数值大小成正比．设群体大小为n ，个体i 的适应度为f_i ，则个体i 被选中遗传到下一代群体的概率为：

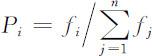
B　遗传算子——交叉（crossover）

所谓交叉运算，是指对两个个体的部分基因依据交叉概率按某种方式相互交换其部分，从而形成两个新的个体．交叉运算在GA中起关键作用，是产生新个体的主要方法．

B1　单交叉点法

选择一个交叉点，子代在交叉点前面的基因从一个父代基因那里得到，后面的部分从另外一个父代基因那里得到．（一般用于二进制编码）

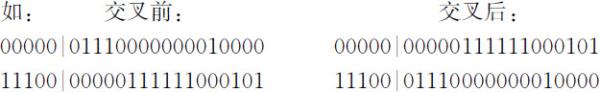
B2　双交叉点法

选择两个交叉点，子代基因在两个交叉点间部分来自一个父代基因，其余部分来自于另外一个父代基因．（一般用于二进制编码）

B3　“与／或”交叉法（用于二进制编码）

对父代按位“与”逻辑运算产生一子代A；按位“或”逻辑运算产生另一子代B．该交叉策略在解背包问题中效果较好．（一般用于二进制编码）

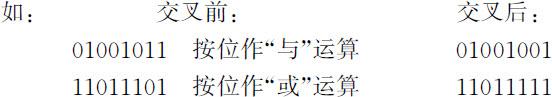
C　遗传算子——变异（mutation）

变异是指依据变异概率将个体编码串中的某些基因值用其他基因值来替换，从而形成一个新的个体．对于二进制编码来说，变异是将某个位的0变为1，或将某个位的1变为0．GA中的变异运算是产生新个体的辅助方法，它决定了GA的局部搜索能力，同时保持种群的多样性．交叉运算和变异运算的相互配合，共同完成对搜索空间的全局搜索和局部搜索．

变异概率P_m 不能太小，这样降低全局搜索能力；也不能太大，当P_m >0.5时GA退化为随机搜索．

7.1.5　运行参数

GA运行时选择的参数应该视解决的具体问题而定，到目前为止，还没有一个适用于GA所有应用领域的关于算法参数的理论．下面是一般情况下使用GA时推荐的参数：

A编码长度：每个个体的编码串（Encoded String）的大小．

B种群规模：种群规模指的是群体中个体的个数．实验发现，比较大的种群的规模并不能优化遗传算法的结果．一些研究表明，种群规模的大小取决于编码的方法．

C交叉率：交叉率一般来说应该比较大，推荐使用80％～95％．

D变异率：变异率一般来说应该比较小，一般使用0.5％～1％最好．

E遗传运算的终止进化代数：可以简单地根据经验固定进化的代数．但如果系统已经收敛到一个个体，应该提前终止．

7.1.6　GA的特点

遗传算法的优点：

（1）群体搜索，易于并行化处理；

（2）不是盲目穷举，而是启发式搜索；

（3）适应度函数不受连续、可微等条件的约束，适用范围很广；

（4）容易实现．

一旦有了一个遗传算法的程序，如果想解决一个新的问题，只需针对新的问题重新进行基因编码就行；如果编码方法也相同，那只需要改变一下适应度函数就可以了．

遗传算法主要的缺点是全局搜索能力不强，很容易陷入局部最优解．

7.1.7　GA流程

遗传算法流程图如图7.1所示．

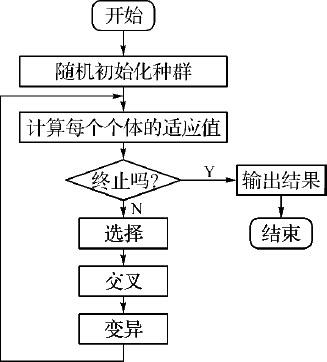
图7.1　遗传算法流程图