5.2 数值和字符处理函数
本节我们将综述R中作为数据处理基石的函数,它们可分为数值(数学、统计、概率)函数和字符处理函数。在阐述过每一类函数以后,我将为你展示如何将函数应用到矩阵和数据框的列(变量)和行(观测)上(参见5.2.6节)。
5.2.1 数学函数
表5-2列出了常用的数学函数和简短的用例。 表5-2 数学函数
| 函 数 | 描 述 |
|---|---|
abs(x) | 绝对值
abs(-4)返回值为4 |
sqrt(x) | 平方根sqrt(25)返回值为5
和25^(0.5)等价 |
ceiling(x) | 不小于x的最小整数
ceiling(3.475)返回值为4 |
floor(x) | 不大于x的最大整数
floor(3.475)返回值为3 |
trunc(x) | 向 0 的方向截取的x中的整数部分
trunc(5.99)返回值为5 |
round(x, digits=n) | 将x舍入为指定位的小数
round(3.475, digits=2)返回值为3.48 |
signif(x, digits=n) | 将x舍入为指定的有效数字位数
signif(3.475, digits=2)返回值为3.5 |
cos(x)、sin(x) 、tan(x) | 余弦、正弦和正切
cos(2)返回值为–0.416 |
acos(x) 、asin(x) 、atan(x) | 反余弦、反正弦和反正切
acos(-0.416)返回值为2 |
cosh(x) 、sinh(x) 、tanh(x) | 双曲余弦、双曲正弦和双曲正切
sinh(2)返回值为3.627 |
acosh(x) 、asinh(x) 、atanh(x) | 反双曲余弦、反双曲正弦和反双曲正切
asinh(3.627)返回值为2 |
log(x,base=n)
log(x)
log10(x) | 对x取以n为底的对数
为了方便起见
log(x)为自然对数
log10(x)为常用对数
log(10)返回值为2.3026
log10(10)返回值为1 |
exp(x) | 指数函数
exp(2.3026)返回值为10 |
对数据做变换是这些函数的一个主要用途。例如,你经常会在进一步分析之前将收入这种存在明显偏倚的变量取对数。数学函数也被用作公式中的一部分,用于绘图函数(例如x 对 sin(x))和在输出结果之前对数值做格式化。
表5-2中的示例将数学函数应用到了标量(单独的数值)上。当这些函数被应用于数值向量、矩阵或数据框时,它们会作用于每一个独立的值。例如,sqrt(c(4, 16, 25))的返回值为c(2, 4, 5)。
5.2.2 统计函数
常用的统计函数如表5-3所示,其中许多函数都拥有可以影响输出结果的可选参数。举例来说:
y <- mean(x)
提供了对象x中元素的算术平均数,而:
z <- mean(x, trim = 0.05, na.rm=TRUE)
则提供了截尾平均数,即丢弃了最大5%和最小5%的数据和所有缺失值后的算术平均数。请使用help()了解以上每个函数和其参数的用法。
表5-3 统计函数
| 函 数 | 描 述 |
|---|---|
mean(x) | 平均数
mean(c(1,2,3,4))返回值为2.5 |
median(x) | 中位数
median(c(1,2,3,4))返回值为2.5 |
sd(x) | 标准差
sd(c(1,2,3,4))返回值为1.29 |
var(x) | 方差
var(c(1,2,3,4))返回值为1.67 |
mad(x) | 绝对中位差(median absolute deviation)
mad(c(1,2,3,4))返回值为1.48 |
quantile(x,probs) | 求分位数。其中x为待求分位数的数值型向量,probs为一个由[0,1]之间的概率值组成的数值向量
# 求x的30%和84%分位点
y <- quantile(x, c(.3,.84)) |
range(x) | 求值域
x <- c(1,2,3,4)
range(x)返回值为c(1,4)
diff(range(x))返回值为3 |
sum(x) | 求和
sum(c(1,2,3,4))返回值为10 |
diff(x, lag=n) | 滞后差分,lag用以指定滞后几项。默认的lag值为1
x<- c(1, 5, 23, 29)
diff(x)返回值为c(4, 18, 6) |
min(x) | 求最小值
min(c(1,2,3,4))返回值为1 |
max(x) | 求最大值
max(c(1,2,3,4))返回值为4 |
scale(x,center=TRUE, scale=TRUE) | 为数据对象x按列进行中心化(center=TRUE)或标准化(center=TRUE,scale=TRUE);
代码清单5-6中给出了一个示例 |
要了解这些函数的实战应用,请参考代码清单5-1。这段代码演示了计算某个数值向量的均值和标准差的两种方式。
代码清单5-1 均值和标准差的计算
> x <- c(1,2,3,4,5,6,7,8)> mean(x) # 简洁的方式[1] 4.5> sd(x)[1] 2.449490> n <- length(x) # 冗长的方式> meanx <- sum(x)/n> css <- sum((x - meanx)^2)> sdx <- sqrt(css / (n-1))> meanx[1] 4.5> sdx[1] 2.449490
第二种方式中修正平方和(css)的计算过程是很有启发性的:
x等于c(1, 2, 3, 4, 5, 6, 7, 8),x的平均值等于4.5(length(x)返回了x中元素的数量);(x – meanx)从x的每个元素中减去了4.5,结果为c(-3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5);(x – meanx)^2将(x - meanx)的每个元素求平方,结果为c(12.25, 6.25, 2.25, 0.25, 0.25, 2.25, 6.25, 12.25);sum((x - meanx)^2)对(x - meanx)^2)的所有元素求和,结果为42。
R中公式的写法和类似MATLAB的矩阵运算语言有着许多共同之处。(我们将在附录E中具体关注解决矩阵代数问题的方法。)
数据的标准化
默认情况下,函数scale()对矩阵或数据框的指定列进行均值为0、标准差为1的标准化:
newdata <- scale(mydata)
要对每一列进行任意均值和标准差的标准化,可以使用如下的代码:
- newdata <- scale(mydata)*SD + M
其中的M是想要的均值,SD为想要的标准差。在非数值型的列上使用scale()函数将会报错。要对指定列而不是整个矩阵或数据框进行标准化,你可以使用这样的代码:
newdata <- transform(mydata, myvar = scale(myvar)*10+50)
此句将变量myvar标准化为均值50、标准差为10的变量。我们将在5.3节数据处理问题的解决方法中用到scale()函数。
5.2.3 概率函数
你可能在疑惑为何概率函数未和统计函数列在一起。(你真的对此有些困惑,对吧?)虽然根据定义,概率函数也属于统计类,但是它们非常独特,应独立设一节进行讲解。概率函数通常用来生成特征已知的模拟数据,以及在用户编写的统计函数中计算概率值。
在R中,概率函数形如1:
1 其中distribution_abbreviation()指分布名称的缩写。——译者注
- [dpqr]distribution_abbreviation()
其中第一个字母表示其所指分布的某一方面:
d = 密度函数(density)
p = 分布函数(distribution function)
q = 分位数函数(quantile function)
r = 生成随机数(随机偏差)
常用的概率函数列于表5-4中。 表5-4 概率分布
| 分布名称 | 缩 写 |
|---|---|
| Beta分布 | beta |
| 二项分布 | binom |
| 柯西分布 | cauchy |
| (非中心)卡方分布 | chisq |
| 指数分布 | exp |
| F分布 | f |
| Gamma分布 | gamma |
| 几何分布 | geom |
| 超几何分布 | hyper |
| 对数正态分布 | lnorm |
| Logistic分布 | logis |
| 多项分布 | multinom |
| 负二项分布 | nbinom |
| 正态分布 | norm |
| 泊松分布 | pois |
| Wilcoxon符号秩分布 | signrank |
| t分布 | t |
| 均匀分布 | unif |
| Weibull分布 | weibull |
| Wilcoxon秩和分布 | wilcox |
我们不妨先看看正态分布的有关函数,以了解这些函数的使用方法。如果不指定一个均值和一个标准差,则函数将假定其为标准正态分布(均值为0,标准差为1)。密度函数(dnorm)、分布函数(pnorm)、分位数函数(qnorm)和随机数生成函数(rnorm)的使用示例见表5-5。
表5-5 正态分布函数
| 问 题 | 解 法 |
|---|---|
在区间[-3, 3]上绘制标准正态曲线
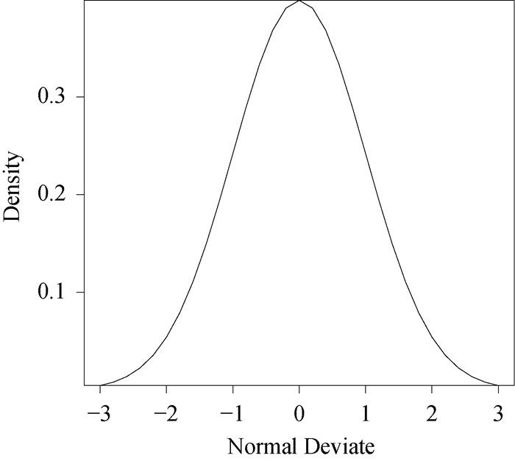 |
|
| 位于 z=1.96 左侧的标准正态曲线下方面积是多少? | pnorm(1.96)等于0.975 |
| 均值为500,标准差为100的正态分布的0.9分位点值为多少? | qnorm(.9, mean=500, sd=100)等于628.16 |
| 生成50个均值为50,标准差为10的正态随机数 | rnorm(50, mean=50, sd=10) |
如果读者对绘图函数的选项不熟悉,请不要担心。这些选项在第11章中有详述。pretty()在本章稍后的表5-7中进行了解释。
- 设定随机数种子
在每次生成伪随机数的时候,函数都会使用一个不同的种子,因此也会产生不同的结果。你可以通过函数set.seed()显式指定这个种子,让结果可以重现(reproducible)。代码清单5-2给出了一个示例。这里的函数runif()用来生成0到1区间上服从均匀分布的伪随机数。
代码清单5-2 生成服从正态分布的伪随机数
> runif(5)[1] 0.8725344 0.3962501 0.6826534 0.3667821 0.9255909> runif(5)[1] 0.4273903 0.2641101 0.3550058 0.3233044 0.6584988> set.seed(1234)> runif(5)[1] 0.1137034 0.6222994 0.6092747 0.6233794 0.8609154> set.seed(1234)> runif(5)[1] 0.1137034 0.6222994 0.6092747 0.6233794 0.8609154
通过手动设定种子,就可以重现你的结果了。这种能力有助于我们创建会在未来取用的,以及可与他人分享的示例。
- 生成多元正态数据
在模拟研究和蒙特卡洛方法中,你经常需要获取来自给定均值向量和协方差阵的多元正态分布的数据。MASS包中的mvrnorm()函数可以让这个问题变得很容易。其调用格式为:
- mvrnorm(n, mean, sigma)
其中n是你想要的样本大小,mean为均值向量,而sigma是方差-协方差矩阵(或相关矩阵)。在代码清单5-3中,你将从一个参数如下所示的三元正态分布中抽取500个观测。
| 均值向量 | 230.7 | 146.7 | 3.6 |
| 协方差阵 | 15360.8
6721.2
-47.1 | 6721.2
4700.9
-16.5 | -47.1
-16.5
0.3 |
代码清单5-3 生成服从多元正态分布的数据
> library(MASS)> options(digits=3)> set.seed(1234) # ❶ 设定随机数种子> mean <- c(230.7, 146.7, 3.6) # ❷ 指定均值向量、协方差阵> sigma <- matrix(c(15360.8, 6721.2, -47.1,6721.2, 4700.9, -16.5,-47.1, -16.5, 0.3), nrow=3, ncol=3)> mydata <- mvrnorm(500, mean, sigma) # ❸ 生成数据> mydata <- as.data.frame(mydata)> names(mydata) <- c("y","x1","x2")> dim(mydata) # ❹ 查看结果[1] 500 3> head(mydata, n=10)y x1 x21 98.8 41.3 4.352 244.5 205.2 3.573 375.7 186.7 3.694 -59.2 11.2 4.235 313.0 111.0 2.916 288.8 185.1 4.187 134.8 165.0 3.688 171.7 97.4 3.819 167.3 101.0 4.0110 121.1 94.5 3.76
代码清单5-3中设定了一个随机数种子,这样就可以在之后重现结果❶。你指定了想要的均值向量和方差—协方差阵❷,并生成了500个伪随机观测❸。为了方便,结果从矩阵转换为数据框,并为变量指定了名称。最后,你确认了拥有500个观测和3个变量,并输出了前10个观测❹。请注意,由于相关矩阵同时也是协方差阵,所以其实可以直接指定相关关系的结构。
R中的概率函数允许生成模拟数据,这些数据是从服从已知特征的概率分布中抽样而得的。近年来,依赖于模拟数据的统计方法呈指数级增长,在后续各章中会有若干示例。
5.2.4 字符处理函数
数学和统计函数是用来处理数值型数据的,而字符处理函数可以从文本型数据中抽取信息,或者为打印输出和生成报告重设文本的格式。举例来说,你可能希望将某人的姓和名连接在一起,并保证姓和名的首字母大写,抑或想统计可自由回答的调查反馈信息中含有秽语的实例(instance)数量。一些最有用的字符处理函数见表5-6。 表5-6 字符处理函数
| 函 数 | 描 述 |
|---|---|
nchar(x) | 计算x中的字符数量
x <- c("ab", "cde",
"fghij")
length(x)返回值为 3 (参见表5-7)
nchar(x[3])返回值为5 |
substr(x, start, stop) | 提取或替换一个字符向量中的子串
x <- "abcdef"
substr(x, 2, 4)返回值为"bcd"
substr(x, 2, 4) <- "22222"(x将变成"a222ef") |
grep(pattern, x, ignore. case=FALSE, fixed=FALSE) | 在x中搜索某种模式。若fixed=FALSE,则pattern为一个正则表达式。若fixed=TRUE,则pattern为一个文本字符串。返回值为匹配的下标
grep("A",c("b","A","c"),fixed=TRUE)返回值为2 |
sub(pattern, replacement, x, ignore.case=FALSE, fixed=FALSE) | 在x中搜索pattern,并以文本replacement将其替换。若fixed=FALSE,则pattern为一个正则表达式。若fixed=TRUE,则pattern为一个文本字符串
sub("\s",".","Hello There")返回值为Hello.There。
注意,"\s"是一个用来查找空白的正则表达式;使用"\s"而不用"\"的原因是,后者是R中的转义字符(参见1.3.3节) |
strsplit(x, split, fixed=FALSE) | 在split处分割字符向量x中的元素。若fixed=FALSE,则pattern为一个正则表达式。若fixed=TRUE,则pattern为一个文本字符串
y <- strsplit("abc", "")将返回一个含有1个成分、3个元素的列表,包含的内容为"a" "b" "c"
unlist(y)[2]和sapply(y, "[", 2)均会返回"b" |
paste(…, sep="") | 连接字符串,分隔符为sep
paste("x", 1:3,sep="")返回值为c("x1", "x2", "x3")
paste("x",1:3,sep="M")返回值为c("xM1","xM2" "xM3")
paste("Today is", date())返回值为Today is Thu Jun 25 14:17:32 2011(我修改了日期以让它看起来更接近当前的时间) |
toupper(x) | 大写转换
toupper("abc")返回值为"ABC" |
tolower(x) | 小写转换
tolower("ABC")返回值为"abc" |
请注意,函数grep()、sub()和strsplit()能够搜索某个文本字符串(fixed=TRUE)或某个正则表达式(fixed=FALSE,默认值为FALSE)。正则表达式为文本模式的匹配提供了一套清晰而简练的语法。例如,正则表达式:
^[hc]?at
可匹配任意以0个或1个h或c开头、后接at的字符串。因此,此表达式可以匹配hat、cat和at,但不会匹配bat。要了解更多,请参考维基百科的regular expression(正则表达式)条目。
5.2.5 其他实用函数
表5-7中的函数对于数据管理和处理同样非常实用,只是它们无法清楚地划入其他分类中。 表5-7 其他实用函数
| 函 数 | 描 述 |
|---|---|
length(x) | 对象x的长度
x <- c(2, 5, 6, 9)
length(x)返回值为4 |
seq(from, to, by) | 生成一个序列
indices <- seq(1,10,2)
indices的值为c(1, 3, 5, 7, 9) |
rep(x, n) | 将x重复n次
y <- rep(1:3, 2)
y的值为c(1, 2, 3, 1, 2, 3) |
cut(x, n) | 将连续型变量x分割为有着n个水平的因子
使用选项ordered_result = TRUE以创建一个有序型因子 |
pretty(x, n) | 创建美观的分割点。通过选取n+1个等间距的取整值,将一个连续型变量x分割为n个区间。绘图中常用 |
cat(… , file ="myfile", append =FALSE) | 连接…中的对象,并将其输出到屏幕上或文件中(如果声明了一个的话)
|
表中的最后一个例子演示了在输出时转义字符的使用方法。\n表示新行,\t为制表符,\'为单引号,\b为退格,等等。(键入?Quotes以了解更多。)例如,代码:
name <- "Bob"cat( "Hello", name, "\b.\n", "Isn\'t R", "\t", "GREAT?\n")
可生成:
Hello Bob.Isn't R GREAT?
请注意第二行缩进了一个空格。当cat输出连接后的对象时,它会将每一个对象都用空格分开。这就是在句号之前使用退格转义字符(\b)的原因。不然,生成的结果将是“Hello Bob .”。
在数值、字符串和向量上使用我们最近学习的函数是直观而明确的,但是如何将它们应用到矩阵和数据框上呢?这就是下一节的主题。
5.2.6 将函数应用于矩阵和数据框
R函数的诸多有趣特性之一,就是它们可以应用到一系列的数据对象上,包括标量、向量、矩阵、数组和数据框。代码清单5-4提供了一个示例。
代码清单5-4 将函数应用于数据对象
> a <- 5> sqrt(a)[1] 2.236068> b <- c(1.243, 5.654, 2.99)> round(b)[1] 1 6 3> c <- matrix(runif(12), nrow=3)> c[,1] [,2] [,3] [,4][1,] 0.4205 0.355 0.699 0.323[2,] 0.0270 0.601 0.181 0.926[3,] 0.6682 0.319 0.599 0.215> log(c)[,1] [,2] [,3] [,4][1,] -0.866 -1.036 -0.358 -1.130[2,] -3.614 -0.508 -1.711 -0.077[3,] -0.403 -1.144 -0.513 -1.538> mean(c)[1] 0.444
请注意,在代码清单5-4中对矩阵c求均值的结果为一个标量(0.444)。函数mean()求得的是矩阵中全部12个元素的均值。但如果希望求的是各行的均值或各列的均值呢?
R中提供了一个apply()函数,可将一个任意函数“应用”到矩阵、数组、数据框的任何维度上。apply函数的使用格式为:
- apply(x, MARGIN, FUN, ...)
其中,x为数据对象,MARGIN是维度的下标,FUN是由你指定的函数,而…则包括了任何想传递给FUN的参数。在矩阵或数据框中,MARGIN=1表示行,MARGIN=2表示列。请看代码清单5-5中的例子。
代码清单5-5 将一个函数应用到矩阵的所有行(列)
> mydata <- matrix(rnorm(30), nrow=6) # ❶ 生成数据> mydata[,1] [,2] [,3] [,4] [,5][1,] 0.71298 1.368 -0.8320 -1.234 -0.790[2,] -0.15096 -1.149 -1.0001 -0.725 0.506[3,] -1.77770 0.519 -0.6675 0.721 -1.350[4,] -0.00132 -0.308 0.9117 -1.391 1.558[5,] -0.00543 0.378 -0.0906 -1.485 -0.350[6,] -0.52178 -0.539 -1.7347 2.050 1.569> apply(mydata, 1, mean) # ❷ 计算每行的均值[1] -0.155 -0.504 -0.511 0.154 -0.310 0.165> apply(mydata, 2, mean) # ❸ 计算每列的均值[1] -0.2907 0.0449 -0.5688 -0.3442 0.1906> apply(mydata, 2, mean, trim=0.2) # ❹ 计算每列的截尾均值[1] -0.1699 0.0127 -0.6475 -0.6575 0.2312
首先生成了一个包含正态随机数的6×5矩阵❶。然后你计算了6行的均值❷,以及5列的均值❸。最后,你计算了每列的截尾均值(在本例中,截尾均值基于中间60%的数据,最高和最低20%的值均被忽略)❹。
FUN可为任意R函数,这也包括你自行编写的函数(参见5.4节),所以apply()是一种很强大的机制。apply()可把函数应用到数组的某个维度上,而lapply()和sapply()则可将函数应用到列表(list)上。你将在下一节中看到sapply(它是lapply的更好用的版本)的一个示例。
你已经拥有了解决5.1节中数据处理问题所需的所有工具,现在,让我们小试身手。
