8.7　深层次分析

让我们来结束本章对于回归模型的讨论，介绍评价模型泛化能力和变量相对重要性的方法。

8.7.1　交叉验证

上一节我们学习了为回归方程选择变量的方法。若你最初的目标只是描述性分析，那么只需要做回归模型的选择和解释。但当目标是预测时，你肯定会问：“这个方程在真实世界中表现如何呢？”提这样的问题本也是无可厚非的。

从定义来看，回归方法本就是用来从一堆数据中获取最优模型参数。对于OLS回归，通过使得预测误差（残差）平方和最小和对响应变量的解释度（R平方）最大，可获得模型参数。由于等式只是最优化已给出的数据，所以在新数据集上表现并不一定好。

在本章开始，我们讨论了一个例子，生理学家想通过个体锻炼的时间和强度、年龄、性别与BMI来预测消耗的卡路里数。如果用OLS回归方程来拟合该数据，那么仅仅是对一个特殊的观测集最大化R平方，但是研究员想用该等式预测一般个体消耗的卡路里数，而不是原始数据。你知道该等式对于新观测样本表现并不一定好，但是预测的损失会是多少呢？你可能并不知道。通过交叉验证法，我们便可以评价回归方程的泛化能力。

所谓交叉验证，即将一定比例的数据挑选出来作为训练样本，另外的样本作保留样本，先在训练样本上获取回归方程，然后在保留样本上做预测。由于保留样本不涉及模型参数的选择，该样本可获得比新数据更为精确的估计。

在k 重交叉验证中，样本被分为k个子样本，轮流将k-1个子样本组合作为训练集，另外1个子样本作为保留集。这样会获得k 个预测方程，记录k 个保留样本的预测表现结果，然后求其平均值。[当n 是观测总数目，k 为n 时，该方法又称作刀切法（jackknifing）。]

bootstrap包中的crossval()函数可以实现k 重交叉验证。在代码清单8-15中，shrinkage()函数对模型的R平方统计量做了k 重交叉验证。

代码清单8-15　R平方的k 重交叉验证

  1. shrinkage <- function(fit, k=10){
  2.   require(bootstrap)
  4.   theta.fit <- function(x,y){lsfit(x,y)}
  5.   theta.predict <- function(fit,x){cbind(1,x)%*%fit$coef}
  7.   x <- fit$model[,2:ncol(fit$model)]
  8.   y <- fit$model[,1]
  10.   results <- crossval(x, y, theta.fit, theta.predict, ngroup=k)
  11.   r2 <- cor(y, fit$fitted.values)^2
  12.   r2cv <- cor(y, results$cv.fit)^2
  13.   cat("Original R-square =", r2, "\n")
  14.   cat(k, "Fold Cross-Validated R-square =", r2cv, "\n")
  15.   cat("Change =", r2-r2cv, "\n")
  16.   }

代码清单8-15中定义了shrinkage()函数，创建了一个包含预测变量和预测值的矩阵，可获得初始R平方以及交叉验证的R平方。（第12章会更详细地讨论自助法。）

对states数据所有预测变量进行回归，然后再用shrinkage()函数做10重交叉验证：

  1. > fit <- lm(Murder ~ Population + Income + Illiteracy + Frost, data=states)
  2. > shrinkage(fit)
  4. Original R-square=0.567
  5. 10 Fold Cross-Validated R-square=0.4481
  6. Change=0.1188

可以看到，基于初始样本的R平方（0.567）过于乐观了。对新数据更好的方差解释率估计是交叉验证后的R平方（0.448）。（注意，观测被随机分配到k 个群组中，因此每次运行shrinkage()函数，得到的结果都会有少许不同。）

通过选择有更好泛化能力的模型，还可以用交叉验证来挑选变量。例如，含两个预测变量（Population和Illiteracy）的模型，比全变量模型R平方减少得更少（0.03 VS 0.12）：

  1. > fit2 <- lm(Murder~Population+Illiteracy,data=states)
  2. > shrinkage(fit2)
  4. Original R-square=0.5668327
  5. 10 Fold Cross-Validated R-square=0.5346871
  6. Change=0.03214554

这使得双预测变量模型显得更有吸引力。

其他情况类似，基于大训练样本的回归模型和更接近于感兴趣分布的回归模型，其交叉验证效果更好。R平方减少得越少，预测则越精确。

8.7.2　相对重要性

本章我们一直都有一个疑问：“哪些变量对预测有用呢？”但你内心真正感兴趣的其实是：“哪些变量对预测最为重要？”潜台词就是想根据相对重要性对预测变量进行排序。这个问题很有实际用处。例如，假设你能对团队组织成功所需的领导特质依据相对重要性进行排序，那么就可以帮助管理者关注他们最需要改进的行为。

若预测变量不相关，过程就相对简单得多，你可以根据预测变量与响应变量的相关系数来进行排序。但大部分情况中，预测变量之间有一定相关性，这就使得评价变得复杂很多。

评价预测变量相对重要性的方法一直在涌现。最简单的莫过于比较标准化的回归系数，它表示当其他预测变量不变时，该预测变量一个标准差的变化可引起的响应变量的预期变化（以标准差单位度量）。在进行回归分析前，可用scale()函数将数据标准化为均值为0、标准差为1的数据集，这样用R回归即可获得标准化的回归系数。（注意，scale()函数返回的是一个矩阵，而lm()函数要求一个数据框，你需要用一个中间步骤来转换一下。）代码和多元回归的结果如下：

  1. > zstates <- as.data.frame(scale(states))
  2. > zfit <- lm(Murder~Population + Income + Illiteracy + Frost, data=zstates)
  3. > coef(zfit)
  5. (Intercept)  Population      Income  Illiteracy       Frost
  6.  -9.406e-17   2.705e-01   1.072e-02   6.840e-01   8.185e-03

此处可以看到，当其他因素不变时，文盲率一个标准差的变化将增加0.68个标准差的谋杀率。根据标准化的回归系数，我们可认为Illiteracy是最重要的预测变量，而Frost是最不重要的。

还有许多其他方法可定量分析相对重要性。比如，可以将相对重要性看做是每个预测变量（本身或与其他预测变量组合）对R平方的贡献。Ulrike Grömping写的relaimpo包涵盖了一些相对重要性的评价方法（http://prof.beuth-hochschule.de/groemping/relaimpo/）。

相对权重（relative weight）是一种比较有前景的新方法，它是对所有可能子模型添加一个预测变量引起的R平方平均增加量的一个近似值（Johnson，2004；Johnson，Lebreton，2004；LeBreton，Tonidandel，2008）。代码清单8-16提供了一个生成相对权重的函数。

代码清单8-16　relweights()函数，计算预测变量的相对权重

  1. relweights <- function(fit,...){
  2.   R <- cor(fit$model)
  3.   nvar <- ncol(R)
  4.   rxx <- R[2:nvar, 2:nvar]
  5.   rxy <- R[2:nvar, 1]
  6.   svd <- eigen(rxx)
  7.   evec <- svd$vectors
  8.   ev <- svd$values
  9.   delta <- diag(sqrt(ev))
  10.   lambda <- evec %*% delta %*% t(evec)
  11.   lambdasq <- lambda ^ 2
  12.   beta <- solve(lambda) %*% rxy
  13.   rsquare <- colSums(beta ^ 2)
  14.   rawwgt <- lambdasq %*% beta ^ 2
  15.   import <- (rawwgt / rsquare) * 100
  16.   lbls <- names(fit$model[2:nvar])
  17.   rownames(import) <- lbls
  18.   colnames(import) <- "Weights"
  19.   barplot(t(import),names.arg=lbls,
  20.      ylab="% of R-Square",
  21.      xlab="Predictor Variables",
  22.      main="Relative Importance of Predictor Variables",
  23.      sub=paste("R-Square=", round(rsquare, digits=3)),
  24.      ...)
  25. return(import)
  26. }

注意　代码清单8-16中的代码改编自Johnson博士提供的SPSS程序。可以参考Johnson（2000，Multivariate Behavioral Research，35，1–19）了解如何推导相对权重。

现将代码清单8-17中的relweights()函数应用到states数据集。

代码清单8-17　relweights()函数的应用

  1. > fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data=states)
  2. > relweights(fit, col="lightgrey")
  4.            Weights
  5. Population   14.72
  6. Illiteracy   59.00
  7. Income        5.49
  8. Frost        20.79

通过图8-19可以看到各个预测变量对模型方差的解释程度（R平方=0.567），Illiteracy解释了59%的R平方，Frost解释了20.79%。根据相对权重法，Illiteracy有最大的相对重要性，余下依次是Frost、Population和Income。

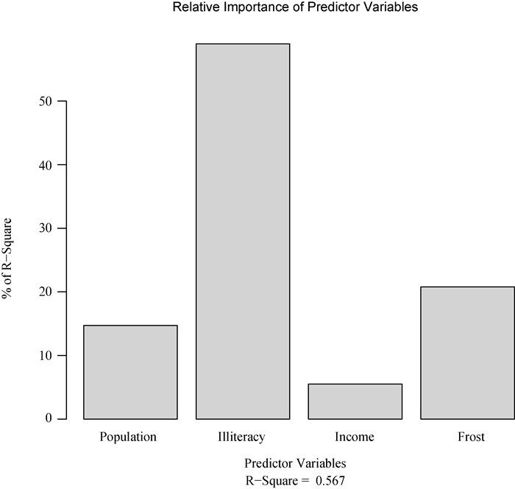
8.7　深层次分析 - 图1

图8-19　states多元回归中各变量相对权重的柱状图

相对重要性的测量（特别是相对权重方法）有广泛的应用，它比标准化回归系数更为直观，我期待将来有更多的人使用它。