12.1 置换检验
置换检验,也称随机化检验或重随机化检验,数十年前就已经被提出,但直到高速计算机的出现,该方法才有了真正的应用价值。
为理解置换检验的逻辑,考虑如下虚拟的问题。有两种处理条件的实验,十个受试者已经被随机分配到其中一种条件(A或B)中,相应的结果变量(score)也已经被记录。实验结果如表12-1所示。
图12-1以带状图形式展示了数据。此时,存在足够的证据说明两种处理方式的影响不同吗? 表12-1 虚拟的两分组问题
| A 处 理 | B 处 理 |
|---|---|
| 40 | 57 |
| 57 | 64 |
| 45 | 55 |
| 55 | 62 |
| 58 | 65 |
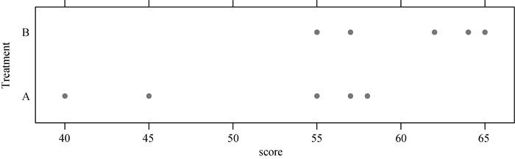
图12-1 表12-1中虚拟数据的带状图
在参数方法中,你可能会假设数据抽样自等方差的正态分布,然后使用假设独立分组的双尾t检验来验证结果。此时,零假设为A处理的总体均值与B处理的总体均值相等,你根据数据计算了t统计量,将其与理论分布进行比较,如果观测到的t统计量值十分极端,比如落在理论分布值的95%置信区间外,那么你将会拒绝零假设,断言在0.05的显著性水平下两组的总体均值不相等。
置换检验的思路与之不同。如果两种处理方式真的等价,那么分配给观测得分的标签(A处理或B处理)便是任意的。为检验两种处理方式的差异,我们可遵循如下步骤:
与参数方法类似,计算观测数据的t统计量,称为t0;
将10个得分放在一个组中;
随机分配五个得分到A处理中,并分配五个得分到B处理中;
计算并记录新观测的t统计量;
对每一种可能随机分配重复(3)~(4)步,此处有252种可能的分配组合;
将252个t统计量按升序排列,这便是基于(或以之为条件)样本数据的经验分布;
如果t0落在经验分布中间95%部分的外面,则在0.05的显著性水平下,拒绝两个处理组的总体均值相等的零假设。
注意,置换方法和参数方法都计算了相同的t统计量。但置换方法并不是将统计量与理论分布进行比较,而是将其与置换观测数据后获得的经验分布进行比较,根据统计量值的极端性判断是否有足够理由拒绝零假设。这种逻辑可以延伸至大部分经典统计检验和线性模型上来。
在先前的例子中,经验分布依据的是数据所有可能的排列组合。此时的置换检验称作“精确”检验。随着样本量的增加,获取所有可能排列的时间开销会非常大,这种情况下,你可以使用蒙特卡洛模拟,从所有可能的排列中进行抽样,获得一个近似的检验。
假如你觉得假定数据成正态分布并不合适,或者担心离群点的影响,又或者感觉对于标准的参数方法来说数据集太小,那么置换检验便提供了一个非常不错的选择。
R目前有一些非常全面而复杂的软件包可以用来做置换检验。本节剩余部分将关注两个有用的包:coin和lmPerm包。第一次使用之前应确保安装了这两个包:
install.packages(c(“coin”,"lmPerm"))
coin对于独立性问题提供了一个非常全面的置换检验的框架,而lmPerm包则专门用来做方差分析和回归分析的置换检验。我们将依次对其进行介绍,并在本节最后简述R中其他可用的用于置换检验的包。
在继续本话题之前,请牢记:置换检验都是使用伪随机数来从所有可能的排列组合中进行抽样(当做近似检验时)。因此,每次检验的结果都有所不同。在R中设置随机数种子便可固定所生成的随机数。这样在你向别人分享自己的示例时,结果便可以重现。设定随机数种子为1234(即set.seed(1234)),可以重现本章所有的结果。
