10.1 假设检验速览
为了帮助你逐步理解功效分析,我们将首先简要回顾统计假设检验的概念。如果你有统计学背景,可直接从10.2节开始阅读。
在统计假设检验中,首先要对总体分布参数设定一个假设(零假设H0),然后从总体分布中抽样,通过样本计算所得的统计量来对总体参数进行推断。假定零假设为真,如果计算获得观测样本的统计量的概率非常小,便可以拒绝原假设,接受它的对立面(称作备择假设或者研究假设H1)。
下面通过一个例子来阐述整个过程。假设你想评价使用手机对驾驶员反应时间的影响,则零假设为H0:μ1-μ2 = 0,μ1是驾驶员使用手机时的反应时间均值,μ2是驾驶员不使用手机时的反应时间均值(此处,μ1-μ2 即感兴趣的总体参数)。假如你拒绝该零假设,备择假设或研究假设就是H1:μ1-μ2 ≠ 0。这等同于μ1 ≠ μ2,即两种条件下反应时间的均值不相等。
现挑选一个由不同个体构成的样本,将他们随机分配到任意一种情况中。第一种情况,参与者边打手机,边在一个模拟器中应对一系列驾驶挑战;第二种情况,参与者在一个模拟器中完成一系列相同的驾驶挑战,但不打手机。然后评估每个个体的总体反应时间。
基于样本数据,可计算如下统计量:
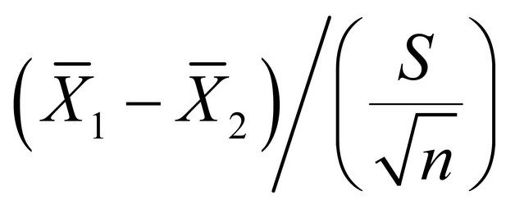
其中,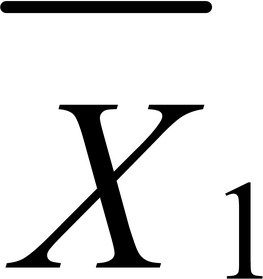 和
和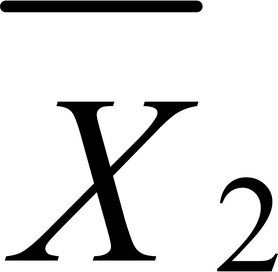 分别表示两种情况下的反应时间均值。S是样本标准差,n是各条件下的参与者数目。如果零假设为真,那么可以假定反应时间呈正态分布,该样本统计量服从2 n-2自由度的t分布。依据此事实,你能计算获得当前或更大样本统计量的概率。但如果概率(p)比预先设定的阈值小(如p<0.05),那么你便可以拒绝原假设接受备择假设。预先约定的阈值(0.05)称为检验的显著性水平(significance level)。
分别表示两种情况下的反应时间均值。S是样本标准差,n是各条件下的参与者数目。如果零假设为真,那么可以假定反应时间呈正态分布,该样本统计量服从2 n-2自由度的t分布。依据此事实,你能计算获得当前或更大样本统计量的概率。但如果概率(p)比预先设定的阈值小(如p<0.05),那么你便可以拒绝原假设接受备择假设。预先约定的阈值(0.05)称为检验的显著性水平(significance level)。
注意,这里是使用取自总体的样本数据来对总体做推断。你的零假设是所有打手机的驾驶员的反应时间均值不同于所有(而不仅仅是你样本中)不打手机的驾驶员的反应时间均值。你的判断有下列四种可能的结果。
如果零假设是错误的,统计检验也拒绝它,那么你便做了一个正确的判断。你可以断言使用手机影响反应时间。
如果零假设是真实的,你没有拒绝它,那么你再次做了一个正确的判断。说明反应时间不受打手机的影响。
如果零假设是真实的,但你却拒绝了它,那么你便犯了I型错误。你会得到使用手机会影响反应时间的结论,而实际上不会。
如果零假设是错误的,而你没有拒绝它,那么你便犯了II型错误。使用手机影响反应时间,但你却没有判断出来。
每种结果的解释见下表。
| 判 断 | |||
|---|---|---|---|
| 拒绝H0 | 不拒绝H0 | ||
| 真实的 | H0为真 | I型错误 | 正确 |
| H0为假 | 正确 | II型错误 |
零假设显著性检验中的争论
零假设显著性检验并不是没有争议的,批评者早就提出了一大堆质疑,特别是有关它在心理学领域中的应用。他们指出对p值存在一个广泛的误解,它依赖的统计显著性比实际显著性大,因此事实上零假设永远不可能为真,对于足够大的样本也总是被拒绝,这会造成许多逻辑上的不一致。
本书不会深度探讨这一主题,有兴趣的读者可以参考Harlow、Mulaik和Steiger的书What If There Were No Significance Tests?(1997)。
在研究过程时,研究者通常关注四个量:样本大小、显著性水平、功效和效应值(见图10-1)。
样本大小指的是实验设计中每种条件/组中观测的数目。
显著性水平(也称为alpha)由I型错误的概率来定义。也可以把它看做是发现效应不发生的概率。
功效通过1减去II型错误的概率来定义。我们可以把它看做是真实效应发生的概率。
效应值指的是在备择或研究假设下效应的量。效应值的表达式依赖于假设检验中使用的统计方法。
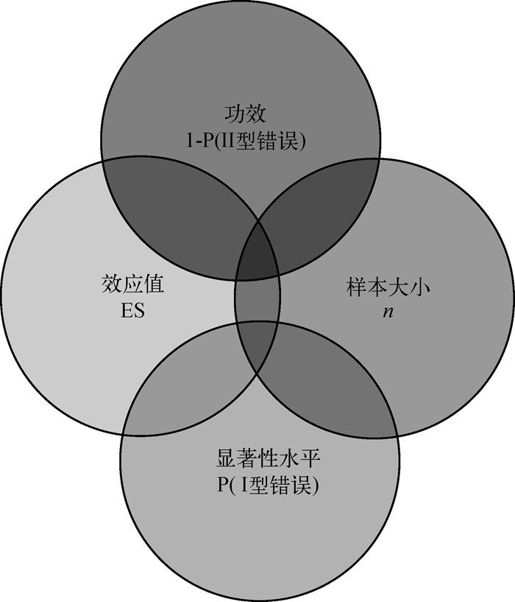
图10-1 在功效分析中研究设计的四个基本量。给定任意三个,你可以推算第四个
虽然研究者可以直接控制样本大小和显著性水平,但是对于功效和效应值的影响却是间接的。例如,放宽显著性水平时(换句话说,使得拒绝原假设更容易时),检验的功效便会增加。类似地,样本量增加,功效也会增加。
通常来说,研究目标是维持一个可接受的显著性水平,尽量使用较少的样本,然后最大化统计检验的功效。也就是说,最大化发现真实效应的几率,并最小化发现错误效应的几率,同时把研究成本控制在合理的范围内。
四个量(样本大小、显著性水平、功效和效应值)紧密相关,给定其中任意三个量,便可推算第四个量。接下来,本章将利用这一点进行各种各样的功效分析。下一节将学习如何用R中的pwr包实现功效分析。随后,我们还会简要回顾一些专门在生物学和遗传学中使用的功效函数。
