第14章　主成分和因子分析

本章内容

• 主成分分析

• 探索性因子分析

• 其他潜变量模型

信息过度复杂是多变量数据最大的挑战之一。若数据集有100个变量，如何了解其中所有的交互关系呢？即使只有20个变量，当试图理解各个变量与其他变量的关系时，也需要考虑190对相互关系。主成分分析和探索性因子分析是两种用来探索和简化多变量复杂关系的常用方法，它们之间有联系也有区别。

主成分分析（PCA）是一种数据降维技巧，它能将大量相关变量转化为一组很少的不相关变量，这些无关变量称为主成分。例如，使用PCA可将30个相关（很可能冗余）的环境变量转化为5个无关的成分变量，并且尽可能地保留原始数据集的信息。

相对而言，探索性因子分析（EFA）是一系列用来发现一组变量的潜在结构的方法。它通过寻找一组更小的、潜在的或隐藏的结构来解释已观测到的、显式的变量间的关系。例如，Harman74.cor包含了24个心理测验间的相互关系，受试对象为145个七年级或八年级的学生。假使应用EFA来探索该数据，结果表明276个测验间的相互关系可用四个学生能力的潜在因子（语言能力、反应速度、推理能力和记忆能力）来进行解释。

PCA与EFA模型间的区别参见图14-1。主成分（PC1和PC2）是观测变量（X1到X5）的线性组合。形成线性组合的权重都是通过最大化各主成分所解释的方差来获得，同时还要保证个主成分间不相关。

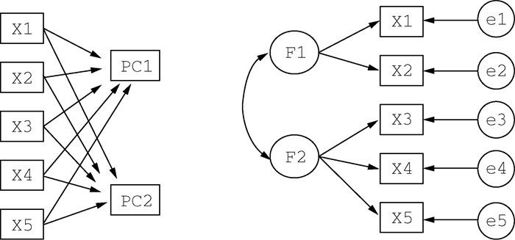
图14-1　主成分分析和因子分析模型。图中展示了可观测变量（X1到X5）、主成分（PC1、PC2）、因子（F1、F2）和误差（e1到e5）

相反，因子（F1和F2）被当做是观测变量的结构基础或“原因”，而不是它们的线性组合。代表观测变量方差的误差（e1到e5）无法用因子来解释。图中的圆圈表示因子和误差无法直接观测，但是可通过变量间的相互关系推导得到。在本例中，因子间带曲线的箭头表示它们之间有相关性。在EFA模型中，相关因子是常见的，但并不是必需的。

本章介绍的两种方法都需要大样本来支撑稳定的结果，但是多大样本量才足够也是一个复杂的问题。目前，数据分析师常使用经验法则：“因子分析需要5～10倍于变量数的样本数。”最近研究表明，所需样本量依赖于因子数目、与各因子相关联的变量数，以及因子对变量方差的解释程度（Bandalos & Boehm-Kaufman，2009）。我将冒险推测一下：如果你有几百个观测，样本量便已充足。本章中，为保证输出结果（和篇幅原因）可控性，我们将人为设定一些小问题。

首先，我们将回顾R中可用来做PCA或EFA的函数，并简略看一看相关分析流程。然后，逐步分析两个PCA示例，以及一个扩展的EFA示例。最后，本章简要列出R中其他拟合潜变量模型的软件包，包括用于验证性因子分析、结构方程模型、对应分析和潜在类别分析的软件包。