15.3　探索缺失值模式

在决定如何处理缺失数据前，了解哪些变量有缺失值、数目有多少、是什么组合形式等信息非常有用。本节中，我们将介绍探索缺失值模式的图表及相关方法。最后，如果知道了数据为何缺失，这将为后续深入研究提供许多启示。

15.3.1　列表显示缺失值

你已经学习了一些识别缺失值的基本方法。比如15.2节使用complete.cases()函数列出完整的实例，或者相反，列出含一个或多个缺失值的实例。但随着数据集的增大，该方法就逐渐丧失了吸引力。此时你可以转向其他R函数。

mice包中的md.pattern()函数可生成一个以矩阵或数据框形式展示缺失值模式的表格。将函数应用到sleep数据集，可得到：

  1. > library(mice)
  2. > data(sleep, package="VIM")
  3. > md.pattern(sleep)
  4.    BodyWgt BrainWgt Pred Exp Danger Sleep Span Gest Dream NonD
  5. 42       1        1    1   1      1     1    1    1     1    1  0
  6.  2       1        1    1   1      1     1    0    1     1    1  1
  7.  3       1        1    1   1      1     1    1    0     1    1  1
  8.  9       1        1    1   1      1     1    1    1     0    0  2
  9.  2       1        1    1   1      1     0    1    1     1    0  2
  10.  1       1        1    1   1      1     1    0    0     1    1  2
  11.  2       1        1    1   1      1     0    1    1     0    0  3
  12.  1       1        1    1   1      1     1    0    1     0    0  3
  13.          0        0    0   0      0     4    4    4    12   14 38

表中1和0显示了缺失值模式，0表示变量的列中有缺失值，1则表示没有缺失值。第一行表述了“无缺失值”的模式（所有元素都为1）。第二行表述了“除了Span之外无缺失值”的模式。第一列表示各缺失值模式的实例个数，最后一列表示各模式中有缺失值的变量的个数。此处可以看到，有42个实例没有缺失值，仅2个实例缺失了Span。9个实例同时缺失了NonD和Dream的值。数据集包含了总共(42 × 0) + (2 × 1) + … + (1 × 3) = 38个缺失值。最后一行给出了每个变量中缺失值的数目。

15.3.2　图形探究缺失数据

虽然md.pattern()函数的表格输出非常简洁，但我通常觉得用图形展示模式更为清晰。VIM包提供了大量能可视化数据集中缺失值模式的函数，本节我们将学习其中几个：aggr()、matrixplot()和scattMiss()。

aggr()函数不仅绘制每个变量的缺失值数，还绘制每个变量组合的缺失值数。例如：

  1. library("VIM")
  2. aggr(sleep, prop=FALSE, numbers=TRUE)

上述代码的结果见图15-2。（VIM包将会打开GUI界面，你可以关闭它；本章我们使用代码完成所有的工作。）

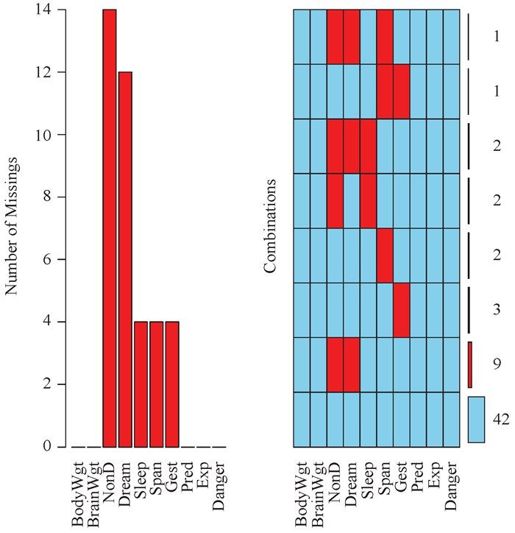
15.3　探索缺失值模式 - 图1

图15-2　aggr()生成的sleep数据集的缺失值模式图形

可以看到，变量NonD有最大的缺失值数（14），有2个哺乳动物缺失了NonD、Dream和Sleep的评分。42个动物没有缺失值。

代码aggr(sleep, prop = TRUE, numbers = TRUE)将生成相同的图形，但用比例代替了计数。选项numbers = FALSE（默认）删去数值型标签。

matrixplot()函数可生成展示每个实例数据的图形。matrixplot(sleep)的图形见图15-3。此处，数值型数据被重新转换到[0, 1]区间，并用灰度来表示大小：浅色表示值小，深色表示值大。默认缺失值为红色。注意，在图15-3中，红色已经被手工阴影化处理，因此相对于灰色缺失值将非常显眼。你可以自己创建图形，让它与众不同。

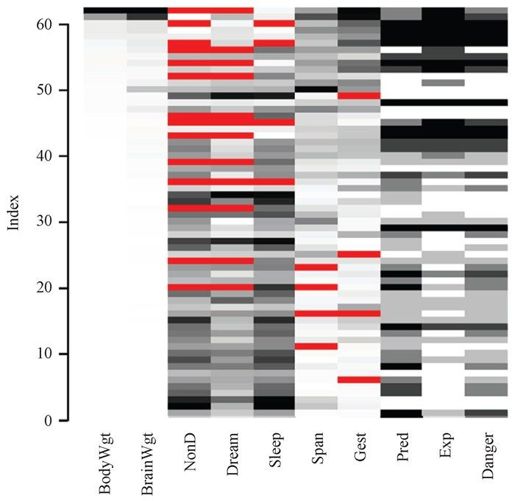
15.3　探索缺失值模式 - 图2

图15-3　sleep数据集按实例（行）展示真实值和缺失值的矩阵图。矩阵按BodyWgt重排

该图形可以进行交互，单击一列将会按其对应的变量重排矩阵。图15-3中的行便按BodyWgt降序排列。通过矩阵图，你可以看出某些变量的缺失值模式是否与其他变量的真实值有关联。此图中可以看到，无缺失值的睡眠变量（Dream、NonD和Sleep）对应着较小的体重（BodyWgt）或脑重（BrainWgt）。

marginplot()函数可生成一幅散点图，在图形边界展示两个变量的缺失值信息。以做梦时长与哺乳动物妊娠期时长的关系为例，来看下列代码：

  1. marginplot(sleep[c("Gest","Dream")], pch=c(20),
  2.            col=c("darkgray", "red", "blue"))

它的生成图形见图15-4。参数pch和col为可选项，控制着绘图符号和使用的颜色。

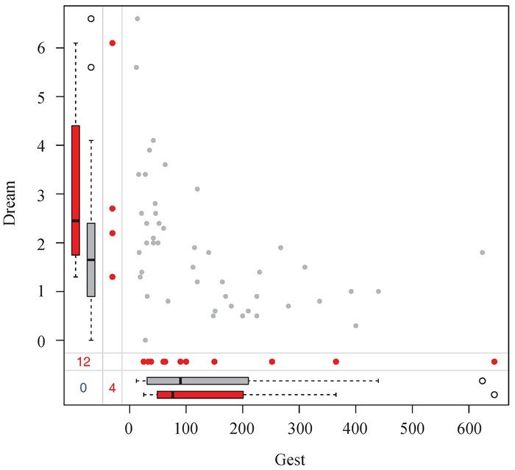
15.3　探索缺失值模式 - 图3

图15-4　做梦时长与妊娠期时长的散点图，边界展示了缺失数据的信息

图形的主体是Gest和Dream（两变量数据都完整）的散点图。左边界的箱线图展示的是包含（深灰色）与不包含（红色）Gest值的Dream变量分布。注意，在灰度图上红色是更深的阴影。四个红色的点代表着缺失了Gest得分的Dream值。在底部边界上，Gest和Dream间的关系反过来了。可以看到，妊娠期和做梦时长呈负相关，缺失妊娠期数据时动物的做梦时长一般更长。两个变量均有缺失值的观测个数在两边界交叉处（左下角）用蓝色输出。

VIM包有许多图形可以帮助你理解缺失数据在数据集中的模式，包括用散点图、箱线图、直方图、散点图矩阵、平行坐标图、轴须图和气泡图来展示缺失值的信息，因此这个包很值得探索。

15.3.3　用相关性探索缺失值

在继续下文之前，还有些方法值得注意。你可用指示变量替代数据集中的数据（1表示缺失，0表示存在），这样生成的矩阵有时称作影子矩阵。求这些指示变量间和它们与初始（可观测）变量间的相关性，有助于观察哪些变量常一起缺失，以及分析变量“缺失”与其他变量间的关系。

考虑如下代码：

  1. x <- as.data.frame(abs(is.na(sleep)))

若sleep的元素缺失，则数据框x对应的元素为1，否则为0。你可以观察下数据的前几行：

  1. > head(sleep, n=5)
  2.    BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
  3. 1 6654.000   5712.0   NA    NA   3.3 38.6  645    3   5      3
  4. 2    1.000      6.6  6.3   2.0   8.3  4.5   42    3   1      3
  5. 3    3.385     44.5   NA    NA  12.5 14.0   60    1   1      1
  6. 4    0.920      5.7   NA    NA  16.5   NA   25    5   2      3
  7. 5 2547.000   4603.0  2.1   1.8   3.9 69.0  624    3   5      4
  9. > head(x, n=5)
  10.   BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
  11. 1       0        0    1     1     0    0    0    0   0      0
  12. 2       0        0    0     0     0    0    0    0   0      0
  13. 3       0        0    1     1     0    0    0    0   0      0
  14. 4       0        0    1     1     0    1    0    0   0      0
  15. 5       0        0    0     0     0    0    0    0   0      0

以下代码：

  1. y <- x[which(sd(x) > 0)]

可提取含（但不全部是）缺失值的变量，而

  1. cor(y)

可列出这些指示变量间的相关系数：

  1.         NonD  Dream  Sleep  Span   Gest
  2. NonD   1.000  0.907  0.486  0.015 -0.142
  3. Dream  0.907  1.000  0.204  0.038 -0.129
  4. Sleep  0.486  0.204  1.000 -0.069 -0.069
  5. Span   0.015  0.038 -0.069  1.000  0.198
  6. Gest  -0.142 -0.129 -0.069  0.198  1.000

此时，你可以看到Dream和NonD常常一起缺失（r = 0.91）。相对可能性较小的是Sleep和NonD一起缺失（r = 0.49），以及Sleep和Dream（r = 0.20）。

最后，你可以看到含缺失值变量与其他可观测变量间的关系：

  1. > cor(sleep, y, use="pairwise.complete.obs")
  2.            NonD  Dream   Sleep   Span   Gest
  3. BodyWgt   0.227  0.223  0.0017 -0.058 -0.054
  4. BrainWgt  0.179  0.163  0.0079 -0.079 -0.073
  5. NonD         NA     NA      NA -0.043 -0.046
  6. Dream    -0.189     NA -0.1890  0.117  0.228
  7. Sleep    -0.080 -0.080      NA  0.096  0.040
  8. Span      0.083  0.060  0.0052     NA -0.065
  9. Gest      0.202  0.051  0.1597 -0.175     NA
  10. Pred      0.048 -0.068  0.2025  0.023 -0.201
  11. Exp       0.245  0.127  0.2608 -0.193 -0.193
  12. Danger    0.065 -0.067  0.2089 -0.067 -0.204
  13. Warning message:
  14. In cor(sleep, y, use = "pairwise.complete.obs") :
  15.   the standard deviation is zero

在这个相关系数矩阵中，行为可观测变量，列为表示缺失的指示变量。你可以忽略矩阵中的警告信息和NA值，这些都是方法中人为因素所导致的。

从相关系数矩阵的第一列可以看到，体重越大（r = 0.227）、妊娠期越长（r =0.202）、睡眠暴露度越大（r = 0.245）的动物无梦睡眠的评分更可能缺失。其他列的信息也可以按类似方式得出。注意，表中的相关系数并不特别大，表明数据是MCAR的可能性比较小，更可能为MAR。

不过也绝不能排除数据是NMAR的可能性，因为你并不知道缺失数据背后对应的真实数据是怎么样的。比如，你不可能知道哺乳动物做梦时长与该变量数据缺失概率间的关系。当缺乏强力的外部证据时，我们通常假设数据是MCAR或者MAR。