12.6　boot包中的自助法

boot包扩展了自助法和重抽样的相关用途。你可以对一个统计量（如中位数）或一个统计量向量（如一列回归系数）使用自助法。使用自助法前请确保下载并安装了boot包：

  1. install.packages("boot")

自助法过程看起来复杂，但你一看例子就会十分明了。

一般来说，自助法有三个主要步骤。

  • 写一个能返回待研究统计量值的函数。如果只有单个统计量（如中位数），函数应该返回一个数值；如果有一列统计量（如一列回归系数），函数应该返回一个向量。

  • 为生成R中自助法所需的有效统计量重复数，使用boot()函数对上面所写的函数进行处理。

  • 使用boot.ci()函数获取第2步生成的统计量的置信区间。

现在举例说明。

主要的自助法函数是boot()，它的格式为：

  1. bootobject <- boot(data=, statistic=, R=, ...)

参数描述见表12-3。 表12-3　boot()函数的参数

参　　数 描　　述
data 向量、矩阵或者数据框
statistic 生成k个统计量以供自举的函数（k=1时对单个统计量进行自助抽样） 函数需包括indices参数，以便boot()函数用它从每个重复中选择实例（例子见下文）
R 自助抽样的次数
… 其他对生成待研究统计量有用的参数，可在函数中传输

boot()函数调用统计量函数R次，每次都从整数1:nrow(data)中生成一列有放回的随机指标，这些指标被统计量函数用来选择样本。统计量将根据所选样本进行计算，结果存储在bootobject中。bootobject结构的描述见表12-4。 表12-4　boot()函数中返回对象所含的元素

元　　素 描　　述
t0 从原始数据得到的k个统计量的观测值
t 一个R × k矩阵，每行即k个统计量的自助重复值

你可以如bootobject$t0和bootobject$t这样来获取这些元素。

一旦生成了自助样本，可通过print()和plot()来检查结果。如果结果看起来还算合理，使用boot.ci()函数获取统计量的置信区间。格式如下：

  1. boot.ci(bootobject, conf=, type= )

参数见表12-5。 表12-5　boot.ci()函数的参数

参　　数 描　　述
bootobject boot()函数返回的对象
conf 预期的置信区间（默认：conf = 0.95）
type 返回的置信区间类型。可能值为norm、basic、stud、perc、bca和all（默认：type = all）

type参数设定了获取置信区间的方法。perc方法（分位数）展示的是样本均值，bca将根据偏差对区间做简单调整。而我发现bca在大部分情况中都是更可取的。参见Mooney和Duval(1993)的书籍，他们对以上方法都有介绍。

本节接下来介绍如何对单个统计量和统计量向量使用自助法。

12.6.1　对单个统计量使用自助法

以1974年Motor Trend杂志中的mtcars数据集为例，它包含32辆汽车的信息。假设你正使用多元回归根据车重（1b/1000）和发动机排量（cu.in.，即立方英寸）来预测汽车每加仑行驶的英里数，除了标准的回归统计量，你还想获得95%的R平方值的置信区间（预测变量对响应变量可解释的方差比），那么便可使用非参数的自助法来获取置信区间。

首要任务是写一个获取R平方值的函数：

  1. rsq <- function(formula, data, indices) {
  2.          d <- data[indices,]
  3.          fit <- lm(formula, data=d)
  4.          return(summary(fit)$r.square)
  5. }

函数返回回归的R平方值。d <- data[indices, ]必须声明，因为boot()要用其来选择样本。

你能做大量的自助抽样（比如1000），代码如下：

  1. library(boot)
  2. set.seed(1234)
  3. results <- boot(data=mtcars, statistic=rsq,
  4.                 R=1000, formula=mpg~wt+disp)

boot的对象可以输出，代码如下：

  1. > print(results)
  3. ORDINARY NONPARAMETRIC BOOTSTRAP
  6. Call:
  7. boot(data = mtcars, statistic = rsq, R = 1000, formula = mpg ~
  8.     wt + disp)
  11. Bootstrap Statistics :
  12.      original     bias    std. error
  13. t1* 0.7809306 0.01333670  0.05068926

也可用plot(results)来绘制结果，图形见图12-2。

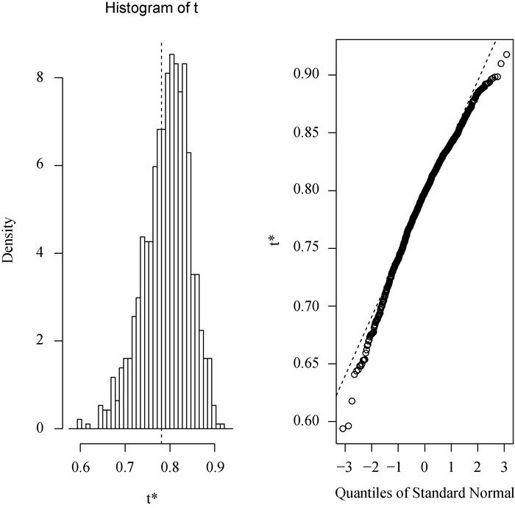
12.6　boot包中的自助法 - 图1

图12-2　自助法所得R平方值的均值

在图12-2中可以看到，自助的R平方值不呈正态分布。它的95%的置信区间可以通过如下代码获得：

  1. > boot.ci(results, type=c("perc", "bca"))
  2. BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
  3. Based on 1000 bootstrap replicates
  5. CALL :
  6. boot.ci(boot.out = results, type = c("perc", "bca"))
  8. Intervals :
  9. Level     Percentile            BCa
  10. 95%   ( 0.6838,  0.8833 )   ( 0.6344,  0.8549 )
  11. Calculations and Intervals on Original Scale
  12. Some BCa intervals may be unstable

从该例可以看到，生成置信区间的不同方法将会导致获得不同的区间。本例中的依偏差调整区间方法与分位数方法稍有不同。两例中，由于0都在置信区间外，零假设H0：R平方值=0都被拒绝。

本节中，我们估计了单个统计量的置信区间，下一节我们将估计多个统计量的置信区间。

12.6.2　多个统计量的自助法

在先前的例子中，自助法被用来估计单个统计量（R平方）的置信区间。继续该例，让我们获取一个统计量向量——三个回归系数（截距项、车重和发动机排量）——95%的置信区间。

首先，创建一个返回回归系数向量的函数：

  1. bs <- function(formula, data, indices) {
  2.         d <- data[indices,]
  3.         fit <- lm(formula, data=d)
  4.         return(coef(fit))
  5. }

然后使用该函数自助抽样1000次：

  1. library(boot)
  2. set.seed(1234)
  3. results <- boot(data=mtcars, statistic=bs,
  4.                 R=1000, formula=mpg~wt+disp)
  5. > print(results)
  6. ORDINARY NONPARAMETRIC BOOTSTRAP
  7. Call:
  8. boot(data = mtcars, statistic = bs, R = 1000, formula = mpg ~
  9.     wt + disp)
  11. Bootstrap Statistics :
  12.     original   bias    std. error
  13. t1*  34.9606  0.137873     2.48576
  14. t2*  -3.3508 -0.053904     1.17043
  15. t3*  -0.0177 -0.000121     0.00879

当对多个统计量自助抽样时，添加一个索引参数，指明plot()和boot.ci()函数所分析bootobject$t的列。在本例中，索引1指截距项，索引2指车重，索引3指发动机排量。如下代码即用于绘制车重结果：

  1. plot(results, index=2)

图形结果见图12-3。

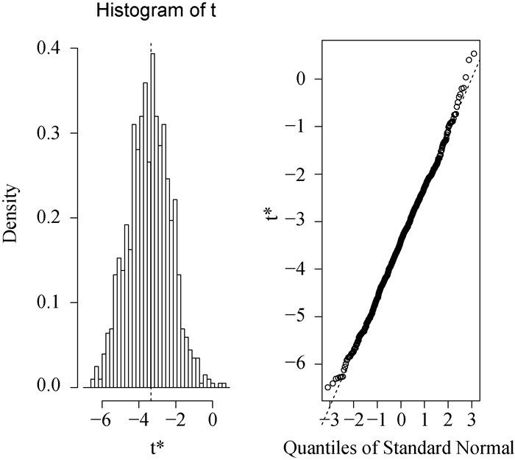
12.6　boot包中的自助法 - 图2

图12-3　自助法所得车重回归系数的分布

为获得车重和发动机排量95%的置信区间，使用代码：

  1. > boot.ci(results, type="bca", index=2)
  2. BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
  3. Based on 1000 bootstrap replicates
  5. CALL :
  6. boot.ci(boot.out = results, type = "bca", index = 2)
  7. Intervals :
  8. Level       BCa
  9. 95%   (-5.66, -1.19 )
  10. Calculations and Intervals on Original Scale
  12. > boot.ci(results, type="bca", index=3)
  14. BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
  15. Based on 1000 bootstrap replicates
  17. CALL :
  18. boot.ci(boot.out = results, type = "bca", index = 3)
  20. Intervals :
  21. Level       BCa
  22. 95%   (-0.0331,  0.0010 )
  23. Calculations and Intervals on Original Scale

注意　在先前例子中，我们每次都对整个样本数据进行重抽样。如果假定预测变量有固定水平（如精心设计的实验），那么我们最好仅对残差项进行重抽样。参考Mooney和Duval（1993，pp.16-17），其中有简单的解释和算法。

在结束自助法介绍前，我们来关注两个常被提出的有价值的问题。

  • 初始样本需要多大？

  • 应该重复多少次？

对于第一个问题，我们无法给出简单的回答。有些人认为只要样本能够较好地代表总体，初始样本大小为20～30即可得到足够好的结果。从感兴趣的总体中随机抽样的方法可信度最高，它能够保证初始样本的代表性。对于第二个问题，我发现1000次重复在大部分情况下都可满足要求。由于计算机资源变得廉价，如果你愿意，也可以增加重复的次数。

置换检验和自助法的信息资源非常丰富。一个非常优秀的入门教程是Yu的在线文章“Resampling Methods: Concepts, Applications, and Justification”（2003）。而Good(2006)则是一份很全面的重抽样概要参考资料，其中包含R代码。关于自助法，Mooney和Duval(1993)给出了一个不错的简介。当然，基础性的自助法资料还是Efron和Tibshirani(1998)的文章。最后，还有许多非常不错的在线资源，比如Simon(1997)、Canty(2002)、Shah(2005)和Fox(2002)。