14.2　主成分分析

PCA的目标是用一组较少的不相关变量代替大量相关变量，同时尽可能保留初始变量的信息，这些推导所得的变量称为主成分，它们是观测变量的线性组合。如第一主成分为：

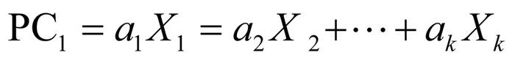
14.2　主成分分析 - 图1

它是k个观测变量的加权组合，对初始变量集的方差解释性最大。第二主成分也是初始变量的线性组合，对方差的解释性排第二，同时与第一主成分正交（不相关）。后面每一个主成分都最大化它对方差的解释程度，同时与之前所有的主成分都正交。理论上来说，你可以选取与变量数相同的主成分，但从实用的角度来看，我们都希望能用较少的主成分来近似全变量集。下面看一个简单的示例。

数据集USJudgeRatings包含了律师对美国高等法院法官的评分。数据框包含43个观测，12个变量。表14-2列出了所有的变量。 表14-2　USJudgeRatings数据集中的变量

变　　量 描　　述
CONT 律师与法官的接触次数
INTG 法官正直程度
DMNR 风度
DILG 勤勉度
CFMG 案例流程管理水平
DECI 决策效率
PREP 审理前的准备工作
FAMI 对法律的熟稔程度
ORAL 口头裁决的可靠度
WRIT 书面裁决的可靠度
PHYS 体能
RTEN 是否值得保留

从实用的角度来看，你是否能够用较少的变量来总结这11个变量（从INTG到RTEN）评估的信息呢？如果可以，需要多少个？如何对它们进行定义呢？因为我们的目标是简化数据，所以可使用PCA。数据保持初始得分的格式，没有缺失值。因此，下一步的决策便是判断需要多少个主成分。

14.2.1　判断主成分的个数

以下是一些可用来判断PCA中需要多少个主成分的准则：

  • 根据先验经验和理论知识判断主成分数；

  • 根据要解释变量方差的积累值的阈值来判断需要的主成分数；

  • 通过检查变量间k × k的相关系数矩阵来判断保留的主成分数。

最常见的是基于特征值的方法。每个主成分都与相关系数矩阵的特征值相关联，第一主成分与最大的特征值相关联，第二主成分与第二大的特征值相关联，依此类推。Kaiser-Harris准则建议保留特征值大于1的主成分，特征值小于1的成分所解释的方差比包含在单个变量中的方差更少。Cattell碎石检验则绘制了特征值与主成分数的图形。这类图形可以清晰地展示图形弯曲状况，在图形变化最大处之上的主成分都可保留。最后，你还可以进行模拟，依据与初始矩阵相同大小的随机数据矩阵来判断要提取的特征值。若基于真实数据的某个特征值大于一组随机数据矩阵相应的平均特征值，那么该主成分可以保留。该方法称作平行分析（详见Hayton、Allen和Scarpello的“Factor Retention Decisions in Exploratory Factor Analysis: A Tutorial on Parallel Analysis”，2004）。

利用fa.parallel()函数，你可以同时对三种特征值判别准则进行评价。对于11种评分（删去了CONT变量），代码如下：

  1. library(psych)
  2. fa.parallel(USJudgeRatings[,-1], fa="PC", n.iter=100,
  3.             show.legend=FALSE, main="Scree plot with parallel analysis")

代码生成图形见图14-2，展示了基于观测特征值的碎石检验（由线段和x符号组成）、根据100个随机数据矩阵推导出来的特征值均值（虚线），以及大于1的特征值准则（y=1的水平线）。

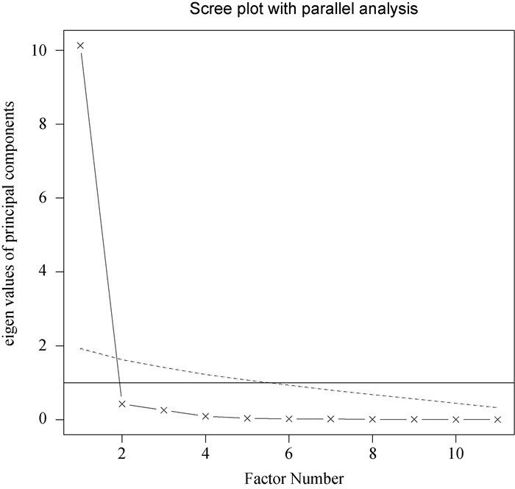
14.2　主成分分析 - 图2

图14-2　评价美国法官评分中要保留的主成分个数。碎石图（直线与x符号）、特征值大于1准则（水平线）和100次模拟的平行分析（虚线）都表明保留一个主成分即可

三种准则表明选择一个主成分即可保留数据集的大部分信息。下一步是使用principal()函数挑选出相应的主成分。

14.2.2　提取主成分

之前已经介绍过，principal()函数可以根据原始数据矩阵或者相关系数矩阵做主成分分析。格式为：

  1. principal(r, nfactors=, rotate=, scores=)

其中：

  • r是相关系数矩阵或原始数据矩阵；

  • nfactors设定主成分数（默认为1）；

  • rotate指定旋转的方法[默认最大方差旋转（varimax），见14.2.3节]。

  • scores设定是否需要计算主成分得分（默认不需要）。

使用代码清单14-1中的代码可获取第一主成分。

代码清单14-1　美国法官评分的主成分分析

  1. > library(psych)
  2. > pc <- principal(USJudgeRatings[,-1], nfactors=1)
  3. > pc
  4. Principal Components Analysis
  5. Call: principal(r = USJudgeRatings[, -1], nfactors=1)
  6. Standardized loadings based upon correlation matrix
  7.       PC1   h2    u2
  8. INTG 0.92 0.84 0.157
  9. DMNR 0.91 0.83 0.166
  10. DILG 0.97 0.94 0.061
  11. CFMG 0.96 0.93 0.072
  12. DECI 0.96 0.92 0.076
  13. PREP 0.98 0.97 0.030
  14. FAMI 0.98 0.95 0.047
  15. ORAL 1.00 0.99 0.009
  16. WRIT 0.99 0.98 0.020
  17. PHYS 0.89 0.80 0.201
  18. RTEN 0.99 0.97 0.028
  20.                  PC1
  21. SS loadings    10.13
  22. Proportion Var  0.92
  23. [… additional output omitted …]

此处，你输入的是没有CONT变量的原始数据，并指定获取一个未旋转（参见14.3.3节）的主成分。由于PCA只对相关系数矩阵进行分析，在获取主成分前，原始数据将会被自动转换为相关系数矩阵 。

PC1栏包含了成分载荷，指观测变量与主成分的相关系数。如果提取不止一个主成分，那么还将会有PC2、PC3等栏。成分载荷（component loadings）可用来解释主成分的含义。此处可以看到，第一主成分（PC1）与每个变量都高度相关，也就是说，它是一个可用来进行一般性评价的维度。

h2栏指成分公因子方差——主成分对每个变量的方差解释度。u2栏指成分唯一性——方差无法被主成分解释的比例（1-h2）。例如，体能（PHYS）80%的方差都可用第一主成分来解释，20%不能。相比而言，PHYS是用第一主成分表示性最差的变量。

SS loadings行包含了与主成分相关联的特征值，指的是与特定主成分相关联的标准化后的方差值（本例中，第一主成分的值为10）。最后，Proportion Var行表示的是每个主成分对整个数据集的解释程度。此处可以看到，第一主成分解释了11个变量92%的方差。

让我们再来看看第二个例子，它的结果不止一个主成分。Harman23.cor数据集包含305个女孩的8个身体测量指标。本例中，数据集由变量的相关系数组成，而不是原始数据集（见表14-3）。 表14-3　305个女孩的身体指标间的相关系数（Harman23.cor）

身　高 指　距 前　臂 小　腿 体　重 股骨转子间径 胸　围 胸　宽
身高 1.00 0.85 0.80 0.86 0.47 0.40 0.30 0.38
指距 0.85 1.00 0.88 0.83 0.38 0.33 0.28 0.41
前臂 0.80 0.88 1.00 0.80 0.38 0.32 0.24 0.34
小腿 0.86 0.83 0.80 1.00 0.44 0.33 0.33 0.36
体重 0.47 0.38 0.38 0.44 1.00 0.76 0.73 0.63
股骨转子间径 0.40 0.33 0.32 0.33 0.76 1.00 0.58 0.58
胸围 0.30 0.28 0.24 0.33 0.73 0.58 1.00 0.54
胸宽 0.38 0.41 0.34 0.36 0.63 0.58 0.54 1.00

* 来源：Harman, H. H. (1976) Modern Factor Analysis, Third Edition Revised, University of Chicago Press, Table 2.3

同样地，我们希望用较少的变量替换这些原始身体指标。如下代码可判断要提取的主成分 数。此处，你需要填入相关系数矩阵（Harman23.cor对象中的cov部分），并设定样本大小（n.obs）：

  1. library(psych)
  2. fa.parallel(Harman23.cor$cov, n.obs=302, fa="pc", n.iter=100
  3.             show.legend=FALSE, main="Scree plot with parallel analysis")

结果见图14-3。

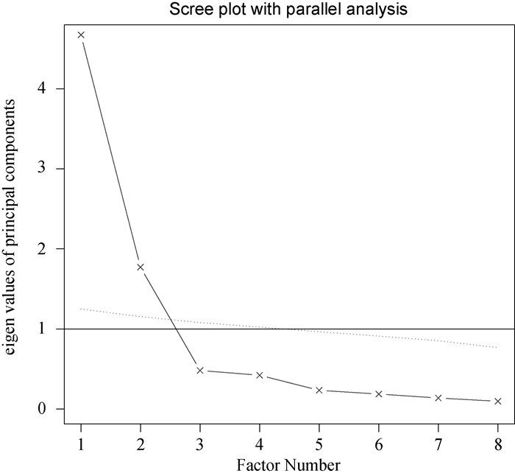
14.2　主成分分析 - 图3

图14-3　判断身体测量数据集所需的主成分数。碎石图（直线和x符号）、特征值大于1准则（水平线）和100次模拟的平行分析建议保留两个主成分

与第一个例子类似，图形中的Kaiser-Harris准则、碎石检验和平行分析都建议选择两个主成分。但是三个准备并不总是相同，你可能需要依据实际情况提取不同数目的主成分，选择最优解决方案。代码清单清单14-2从相关系数矩阵中提取了前两个主成分。

代码清单14-2　身体测量指标的主成分分析

  1. > library(psych)
  2. > PC <- principal(Harman23.cor$cov, nfactors=2, rotate="none")
  3. > PC
  5. Principal Components Analysis
  6. Call: principal(r = Harman23.cor$cov, nfactors = 2, rotate = "none")
  7. Standardized loadings based upon correlation matrix
  8.                 PC1   PC2   h2    u2
  9. height         0.86 -0.37 0.88 0.123
  10. arm.span       0.84 -0.44 0.90 0.097
  11. forearm        0.81 -0.46 0.87 0.128
  12. lower.leg      0.84 -0.40 0.86 0.139
  13. weight         0.76  0.52 0.85 0.150
  14. bitro.diameter 0.67  0.53 0.74 0.261
  15. chest.girth    0.62  0.58 0.72 0.283
  16. chest.width    0.67  0.42 0.62 0.375
  18.                 PC1  PC2
  19. SS loadings    4.67 1.77
  20. Proportion Var 0.58 0.22
  21. Cumulative Var 0.58 0.81
  23. [……已删除额外输出……]

从代码清单14-2中的PC1和PC2栏可以看到，第一主成分解释了身体测量指标58%的方差，而第二主成分解释了22%，两者总共解释了81%的方差。对于高度变量，两者则共解释了其88%的方差。

载荷阵解释了成分和因子的含义。第一主成分与每个身体测量指标都正相关，看起来似乎是一个一般性的衡量因子；第二主成分与前四个变量（height、arm.span、forearm和lower.leg）负相关，与后四个变量（weight、bitro.diameter、chest.girth和chest.width）正相关，因此它看起来似乎是一个长度—容量因子。但理念上的东西都不容易构建，当提取了多个成分时，对它们进行旋转可使结果更具解释性，接下来我们便讨论该问题。

14.2.3　主成分旋转

旋转是一系列将成分载荷阵变得更容易解释的数学方法，它们尽可能地对成分去噪。旋转方法有两种：使选择的成分保持不相关（正交旋转），和让它们变得相关（斜交旋转）。旋转方法也会依据去噪定义的不同而不同。最流行的正交旋转是方差极大旋转，它试图对载荷阵的列进行去噪，使得每个成分只是由一组有限的变量来解释（即载荷阵每列只有少数几个很大的载荷，其他都是很小的载荷）。对身体测量数据使用方差极大旋转，你可以得到如代码清单14-3所示的结果。14.4节将介绍斜交旋转的示例。

代码清单14-3　方差极大旋转的主成分分析

  1. > rc <- principal(Harman23.cor$cov, nfactors=2, rotate="varimax")
  2. > rc
  4. Principal Components Analysis
  5. Call: principal(r = Harman23.cor$cov, nfactors = 2, rotate = "varimax")
  6. Standardized loadings based upon correlation matrix
  7.                 RC1  RC2   h2    u2
  8. height         0.90 0.25 0.88 0.123
  9. arm.span       0.93 0.19 0.90 0.097
  10. forearm        0.92 0.16 0.87 0.128
  11. lower.leg      0.90 0.22 0.86 0.139
  12. weight         0.26 0.88 0.85 0.150
  13. bitro.diameter 0.19 0.84 0.74 0.261
  14. chest.girth    0.11 0.84 0.72 0.283
  15. chest.width    0.26 0.75 0.62 0.375
  17.                 RC1  RC2
  18. SS loadings    3.52 2.92
  19. Proportion Var 0.44 0.37
  20. Cumulative Var 0.44 0.81
  22. [……已删除额外输出……]

列的名字都从PC变成了RC，以表示成分被旋转。观察RC1栏的载荷，你可以发现第一主成分主要由前四个变量来解释（长度变量）。RC2栏的载荷表示第二主成分主要由变量5到变量8来解释（容量变量）。注意两个主成分仍不相关，对变量的解释性不变，这是因为变量的群组没有发生变化。另外，两个主成分旋转后的累积方差解释性没有变化（81%），变的只是各个主成分对方差的解释度（成分1从58%变为44%，成分2从22%变为37%）。各成分的方差解释度趋同，准确来说，此时应该称它们为成分而不是主成分（因为单个主成分方差最大化性质没有保留）。

我们的最终目标是用一组较少的变量替换一组较多的相关变量，因此，你还需要获取每个观测在成分上的得分。

14.2.4　获取主成分得分

在美国法官评分例子中，我们根据原始数据中的11个评分变量提取了一个主成分。利用principal()函数，你很容易获得每个调查对象在该主成分上的得分（见代码清单14-4）。

代码清单14-4　从原始数据中获取成分得分

  1. > library(psych)
  2. > pc <- principal(USJudgeRatings[,-1], nfactors=1, score=TRUE)
  3. > head(pc$scores)
  5.                       PC1
  6. AARONSON,L.H.  -0.1857981
  7. ALEXANDER,J.M.  0.7469865
  8. ARMENTANO,A.J.  0.0704772
  9. BERDON,R.I.     1.1358765
  10. BRACKEN,J.J.   -2.1586211
  11. BURNS,E.B.      0.7669406

当scores = TRUE时，主成分得分存储在principal()函数返回对象的scores元素中。如果有需要，你还可以获得律师与法官的接触频数与法官评分间的相关系数：

  1. > cor(USJudgeRatings$CONT, PC$score)
  2.               PC1
  3. [1,] -0.008815895

显然，律师与法官的熟稔度与律师的评分毫无关联。

当主成分分析基于相关系数矩阵时，原始数据便不可用了，也不可能获取每个观测的主成分得分，但是你可以得到用来计算主成分得分的系数。

在身体测量数据中，你有各个身体测量指标间的相关系数，但是没有305个女孩的个体测量值。按照代码清单14-5，你可得到得分系数。

代码清单14-5　获取主成分得分的系数

  1. > library(psych)
  2. > rc <- principal(Harman23.cor$cov, nfactors=2, rotate="varimax")
  3. > round(unclass(rc$weights), 2)
  4.                  RC1   RC2
  5. height          0.28 -0.05
  6. arm.span        0.30 -0.08
  7. forearm         0.30 -0.09
  8. lower.leg       0.28 -0.06
  9. weight          -0.06 0.33
  10. bitro.diameter  -0.08 0.32
  11. chest.girth     -0.10 0.34
  12. chest.width     -0.04 0.27

利用如下公式可得到主成分得分：

  1. PC1 = 0.28*height + 0.30*arm.span + 0.30*forearm + 0.29*lower.leg -
  2.       0.06*weight - 0.08*bitro.diameter - 0.10*chest.girth -
  3.       0.04*chest.width

和：

  1. PC2 = -0.05*height - 0.08*arm.span - 0.09*forearm - 0.06*lower.leg +
  2.        0.33*weight + 0.32*bitro.diameter + 0.34*chest.girth +
  3.        0.27*chest.width

两个等式都假定身体测量指标都已标准化（mean = 0， sd = 1）。注意，体重在PC1上的系数约为0.3或0，对于PC2也是一样。从实际角度考虑，你可以进一步简化方法，将第一主成分看做是前四个变量标准化得分的均值，类似地，将第二主成分看做是后四个变量标准化得分的均值，这正是我通常在实际中采用的方法。

“小瞬间”（Little Jiffy）征服世界

许多数据分析师都对PCA和EFA存有或多或少的疑惑。一个是历史原因，它可以追溯到一个叫做Little Jiffy的软件（不是玩笑）。Little Jiffy是因子分析早期最流行的一款软件，默认做主成分分析，选用方差极大旋转法，提取特征值大于1的成分。这款软件应用得如此广泛，以至于许多社会科学家都默认它与EFA同义。许多后来的统计软件包在它们的EFA程序中都默认如此处理。

但我希望你通过学习下一节内容发现PCA与EFA间重要的、基础性的不同之处。想更多了解PCA/EFA的混淆点，可参阅Hayton、Allen和Scarpello的“Factor Retention Decisions in Exploratory Factor Analysis: A Tutorial on Parallel Analysis”（2004）。

如果你的目标是寻求可解释观测变量的潜在隐含变量，可使用因子分析，这正是下一节的主题。