8.4　异常观测值

8.4　异常观测值

一个全面的回归分析要覆盖对异常值的分析，包括离群点、高杠杆值点和强影响点。这些数据点需要更深入的研究，因为它们在一定程度上与其他观测点不同，可能对结果产生较大的负面影响。下面我们依次学习这些异常值。

8.4.1　离群点

离群点是指那些模型预测效果不佳的观测点。它们通常有很大的、或正或负的残差（Y_i-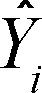 8.4　异常观测值 - 图1 ）。正的残差说明模型低估了响应值，负的残差则说明高估了响应值。

你已经学习过一种鉴别离群点的方法：图8-9的Q-Q图，落在置信区间带外的点即可被认为是离群点。另外一个粗糙的判断准则：标准化残差值大于2或者小于-2的点可能是离群点，需要特别关注。

car包也提供了一种离群点的统计检验方法。outlierTest()函数可以求得最大标准化残差绝对值Bonferroni调整后的p值：

> library(car)
> outlierTest(fit)
     rstudent unadjusted p-value Bonferonni p
Nevada    3.5            0.00095        0.048

此处，你可以看到Nevada被判定为离群点（p=0.048）。注意，该函数只是根据单个最大（或正或负）残差值的显著性来判断是否有离群点。若不显著，则说明数据集中没有离群点；若显著，则你必须删除该离群点，然后再检验是否还有其他离群点存在。

8.4.2　高杠杆值点

高杠杆值观测点，即是与其他预测变量有关的离群点。换句话说，它们是由许多异常的预测变量值组合起来的，与响应变量值没有关系。

高杠杆值的观测点可通过帽子统计量（hat statistic）判断。对于一个给定的数据集，帽子均值为p/n，其中p 是模型估计的参数数目（包含截距项），n 是样本量。一般来说，若观测点的帽子值大于帽子均值的2或3倍，即可以认定为高杠杆值点。下面代码画出了帽子值的分布：

hat.plot <- function(fit) {
              p <- length(coefficients(fit))
              n <- length(fitted(fit))
              plot(hatvalues(fit), main="Index Plot of Hat Values")
              abline(h=c(2,3)*p/n, col="red", lty=2)
              identify(1:n, hatvalues(fit), names(hatvalues(fit)))
            }
hat.plot(fit)

结果见图8-13。

水平线标注的即帽子均值2倍和3倍的位置。定位函数（locator function）能以交互模式绘图：单击感兴趣的点，然后进行标注，停止交互时，用户可按Esc键退出，或从图形下拉菜单中选择Stop，或直接右击图形。此图中，可以看到Alaska和California非常异常，查看它们的预测变量值，与其他48个州进行比较发现：Alaska收入比其他州高得多，而人口和温度却很低；California人口比其他州府多得多，但收入和温度也很高。

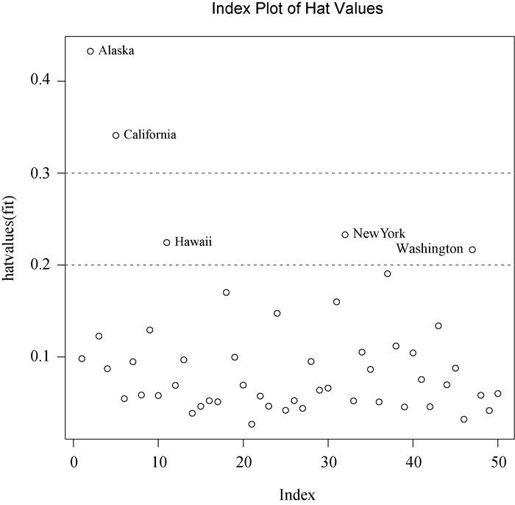
8.4　异常观测值 - 图2

图8-13　用帽子值来判定高杠杆值点

高杠杆值点可能会是强影响点，也可能不是，这要看它们是否是离群点。

8.4.3　强影响点

强影响点，即对模型参数估计值影响有些比例失衡的点。例如，若移除模型的一个观测点时模型会发生巨大的改变，那么你就需要检测一下数据中是否存在强影响点了。

有两种方法可以检测强影响点：Cook距离，或称D统计量，以及变量添加图（added variable plot）。一般来说，Cook's D值大于4/(n-k -1)，则表明它是强影响点，其中n 为样本量大小，k 是预测变量数目。可通过如下代码绘制Cook's D图形（图8-14）：

cutoff <- 4/(nrow(states)-length(fit$coefficients)-2)
plot(fit, which=4, cook.levels=cutoff)
abline(h=cutoff, lty=2, col="red")

通过图形可以判断Alaska、Hawaii和Nevada是强影响点。若删除这些点，将会导致回归模型截距项和斜率发生显著变化。注意，虽然该图对搜寻强影响点很有用，但我逐渐发现以1为分割点比4/(n-k -1)更具一般性。若设定D=1为判别标准，则数据集中没有点看起来像是强影响点。

Cook's D图有助于鉴别强影响点，但是并不提供关于这些点如何影响模型的信息。变量添加图弥补了这个缺陷。对于一个响应变量和k 个预测变量，你可以如下图创建k 个变量添加图。

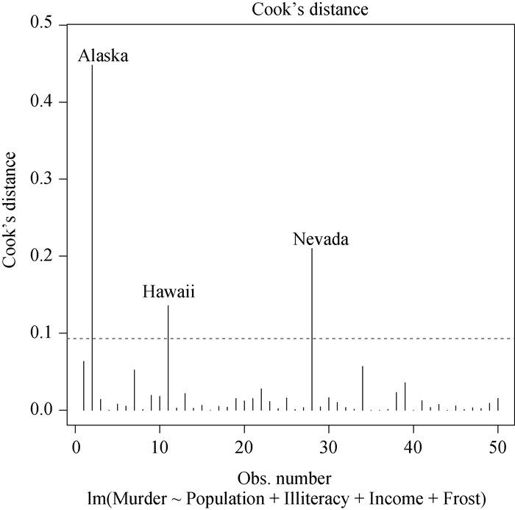
8.4　异常观测值 - 图3

图8-14　鉴别强影响点的Cook's D图

所谓变量添加图，即对于每个预测变量X_k，绘制X_k 在其他k -1个预测变量上回归的残差值相对于响应变量在其他k -1个预测变量上回归的残差值的关系图。car包中的avPlots()函数可提供变量添加图：

library(car)
avPlots(fit, ask=FALSE, onepage=TRUE, id.method="identify")

结果如图8-15所示。图形一次生成一个，用户可以通过单击点来判断强影响点。按下Esc，或从图形菜单中选择Stop，或右击，便可移动到下一个图形。我已在左下图中鉴别出Alaska为强影响点。

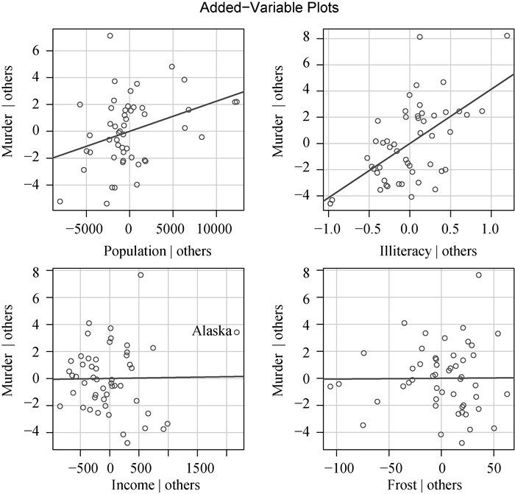
8.4　异常观测值 - 图4

图8-15　评估强影响点影响效果的变量添加图

图中的直线表示相应预测变量的实际回归系数。你可以想象删除某些强影响点后直线的改变，以此来估计它的影响效果。例如，来看左下角的图（“Murder|others” VS“Income|others”），若删除点Alaska，直线将往负向移动。事实上，删除Alaska，Income的回归系数将会从0.000 06变为-0.000 85。

当然，利用car包中的influencePlot()函数，你还可以将离群点、杠杆值和强影响点的信息整合到一幅图形中：

library(car)
influencePlot(fit, id.method="identify", main="Influence Plot",
              sub="Circle size is proportional to Cook’s distance")

图8-16反映出Nevada和Rhode Island是离群点，New York、California、Hawaii和Washington有高杠杆值，Nevada、Alaska和Hawaii为强影响点。

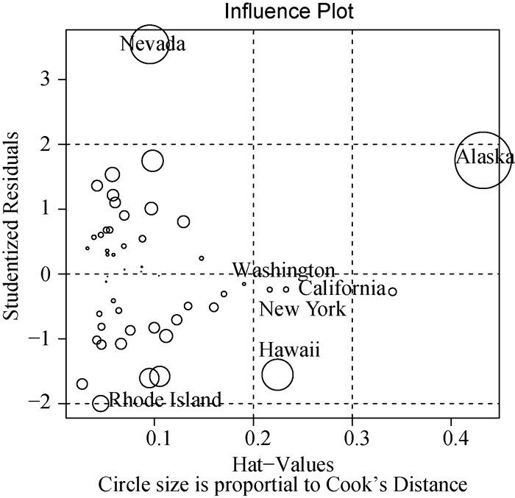
8.4　异常观测值 - 图5

图8-16　影响图。纵坐标超过+2或小于-2的州可被认为是离群点，水平轴超过0.2或0.3的州有高杠杆值（通常为预测值的组合）。圆圈大小与影响成比例，圆圈很大的点可能是对模型参数的估计造成的不成比例影响的强影响点

8.4 异常观测值