11.1　散点图

在之前各章中，我们了解到散点图可用来描述两个连续型变量间的关系。本节，我们首先描述一个二元变量关系（x对y），然后探究各种通过添加额外信息来增强图形表达功能的方法。接着，我们将学习如何把多个散点图组合起来形成一个散点图矩阵，以便可以同时浏览多个二元变量关系。我们还将回顾一些数据点重叠的特殊案例，由于重叠将会削弱图形描述数据的能力，所以我们将围绕该难点讨论多种解决途径。最后，通过添加第三个连续型变量，我们将把二维图形扩展到三维，包括三维散点图和气泡图。它们都可帮助你更好地迅速理解三变量间的多元关系。

R中创建散点图的基础函数是plot(x, y)，其中，x和y是数值型向量，代表着图形中的(x, y)点。代码清单11-1展示了一个例子。

代码清单11-1　添加了最佳拟合曲线的散点图

  1. attach(mtcars)
  2. plot(wt, mpg,
  3.      main="Basic Scatter plot of MPG vs. Weight",
  4.      xlab="Car Weight (lbs/1000)",
  5.      ylab="Miles Per Gallon ", pch=19)
  7. abline(lm(mpg~wt), col="red", lwd=2, lty=1)
  9. lines(lowess(wt,mpg), col="blue", lwd=2, lty=2)

图形结果参见图11-1。

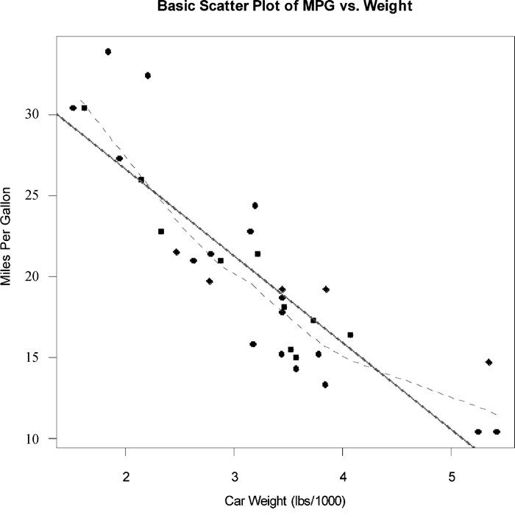
11.1　散点图 - 图1

图11-1　汽车英里数对车重的散点图，添加了线性拟合直线和lowess拟合曲线

代码清单11-1中的代码加载了mtcars数据框，创建了一幅基本的散点图，图形的符号1是实心圆圈。与预期结果相同，随着车重的增加，每加仑英里数减少，虽然它们不是完美的线性关系。abline()函数用来添加最佳拟合的线性直线，而lowess()函数则用来添加一条平滑曲线。该平滑曲线拟合是一种基于局部加权多项式回归的非参数方法。算法细节可参见Cleveland(1981)。

1 即指plot()函数中的pch参数。——译者注

注意　R有两个平滑曲线拟合函数：lowess()和loess()。loess()是基于lowess()表达式版本的更新和更强大的拟合函数。这两个函数的默认值不同，因此要小心使用，不要把它们弄混淆了。

car包中的scatterplot()函数增强了散点图的许多功能，它可以很方便地绘制散点图，并能添加拟合曲线、边界箱线图和置信椭圆，还可以按子集绘图和交互式地识别点。例如，以下代码可生成一个比之前图形更复杂的版本：

  1. library(car)
  2. scatterplot(mpg ~ wt | cyl, data=mtcars, lwd=2,
  3.             main="Scatter Plot of MPG vs. Weight by # Cylinders",
  4.             xlab="Weight of Car (lbs/1000)",
  5.             ylab="Miles Per Gallon",
  6.             legend.plot=TRUE,
  7.             id.method="identify",
  8.             labels=row.names(mtcars),
  9.             boxplots="xy"
  10. )

此处，scatterplot()函数用来绘制有四个、六个和八个气缸的汽车每加仑英里数对车重的图形。表达式mpg ~ wt | cyl表示按条件绘图（即按cyl的水平分别绘制mpg和wt的关系图）。结果见图11-2。

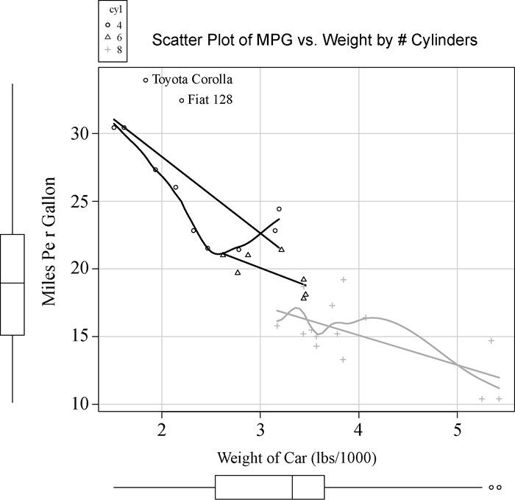
11.1　散点图 - 图2

图11-2　各子集的散点图与其相应的拟合曲线

默认地，各子集会通过颜色和图形符号加以区分，并同时绘制线性拟合和平滑拟合曲线。平滑拟合默认需要五个单独的数据点，因此六缸车型的平滑曲线无法绘制。id.method选项的设定表明可通过鼠标单击来交互式地识别数据点，直到用户选择Stop（通过图形或者背景菜单）或者敲击Esc键。labels选项的设定表明可通过点的行名称来识别点。此图中可以看到，给定Toyata Corolla和Fiat 128的车重，通常每加仑燃油可行驶得更远。legend.plot选项表明在左上边界添加图例，而mpg和weight的边界箱线图可通过boxplots选项来绘制。总之，scatterplot()函数还有许多特性值得探究，比如本节未讨论的稳健性选项和数据集中度椭圆选项。更多细节可参见help(scatterplot)。

散点图可以一次对两个定量变量间的关系进行可视化。但是如果想观察下汽车里程、车重、排量（立方英寸）和后轴比间的二元关系，该怎么做呢？一种途径就是将六幅散点图绘制到一个矩阵中，这便是下节即将介绍的散点图矩阵。

11.1.1　散点图矩阵

R中至少有四种创建散点图矩阵的实用函数。相信数据分析师一定很喜爱散点图矩阵吧？pairs()函数可以创建基础的散点图矩阵。下面的代码生成了一个散点图矩阵，包含mpg、disp、drat和wt四个变量：

  1. pairs(~mpg+disp+drat+wt, data=mtcars,
  2.       main="Basic Scatter Plot Matrix")

图中包含~右边的所有变量，参见图11-3。

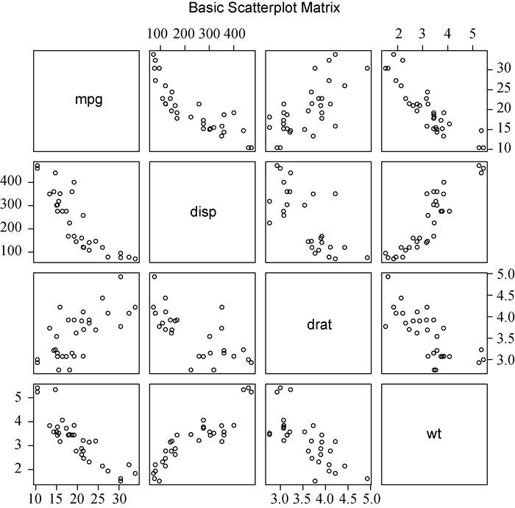
11.1　散点图 - 图3

图11-3　pairs()函数创建的散点图矩阵

在图11-3中，你可以看到所有指定变量间的二元关系。例如，mpg和disp的散点图可在两变量的行列交叉处找到。值得注意的是，主对角线的上方和下方的六幅散点图是相同的，这也是为了方便摆放图形的缘故。通过调整参数，可以只展示下三角或者上三角的图形。例如，选项upper.panel = NULL将只生成下三角的图形。

car包中的scatterplotMatrix()函数也可以生成散点图矩阵，并有以下可选操作：

  • 以某个因子为条件绘制散点图矩阵；

  • 包含线性和平滑拟合曲线；

  • 在主对角线放置箱线图、密度图或者直方图；

  • 在各单元格的边界添加轴须图。

例如：

  1. library(car)
  2. scatterplotMatrix(~ mpg + disp + drat + wt, data=mtcars, spread=FALSE,
  3.                   lty.smooth=2, main="Scatter Plot Matrix via car Package")

结果见图11-4。可以看到线性和平滑（loess）拟合曲线被默认添加，主对角线处添加了核密度曲线和轴须图。spread = FALSE选项表示不添加展示分散度和对称信息的直线，lty.smooth = 2设定平滑（loess）拟合曲线使用虚线而不是实线。

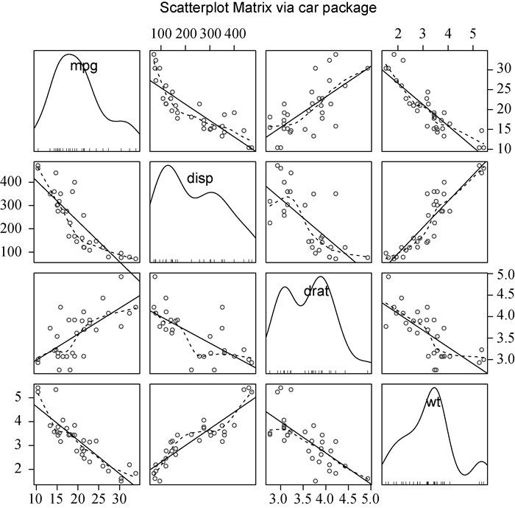
11.1　散点图 - 图4

图11-4　scatterplotMatrix()函数创建的散点图矩阵。主对角线上有核密度曲线和轴须图，其余图形都含有线性和平滑拟合曲线

下面的代码展示了scatterplotMatrix()函数的另一个使用示例：

  1. library(car)
  2. scatterplotMatrix(~ mpg + disp + drat + wt | cyl, data=mtcars,
  3.                   spread=FALSE, diagonal="histogram",
  4.                   main="Scatter Plot Matrix via car Package")

这里，我们将主对角线的核密度曲线改成了直方图，并且直方图是以各车的气缸数为条件绘制的。结果见图11-5。

默认地，回归直线拟合整个样本，包含选项by.groups = TRUE将可依据各子集分别生成拟合曲线。

gclus包中的cpairs()函数提供了一个有趣的散点图矩阵变种。它含有可以重排矩阵中变量位置的选项，可以让相关性更高的变量更靠近主对角线。该函数还能对各单元格进行颜色编码来展示变量间的相关性大小。下面考虑mpg、wt、disp和drat间的相关性：

  1. > cor(mtcars[c("mpg", "wt", "disp", "drat")])
  3.         mpg     wt   disp   drat
  4. mpg   1.000 -0.868 -0.848  0.681
  5. wt   -0.868  1.000  0.888 -0.712
  6. disp -0.848  0.888  1.000 -0.710
  7. drat  0.681 -0.712 -0.710  1.000

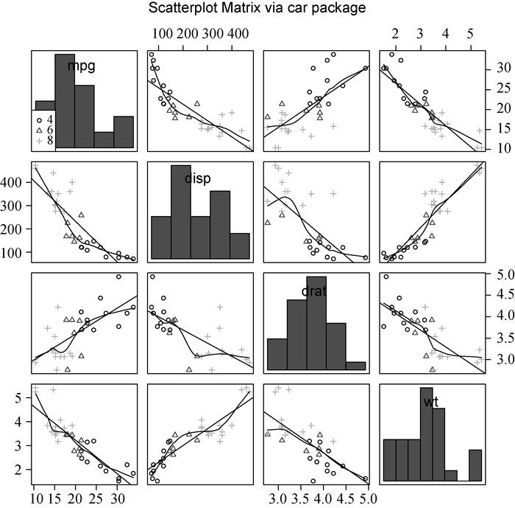
11.1　散点图 - 图5

图11-5　scatterplotMatrix()函数生成的散点图矩阵。图形包含主对角线中的直方图以及其他部分的线性和平滑拟合曲线。另外，子群（根据气缸数）通过符号类型和颜色来区分标注

可以看到相关性最高（0.89）的是车重（wt）与排量（disp），以及车重（wt）与每加仑英里数（mpg；-0.87）。相关性最低（0.68）的是每加仑英里（mpg）与后轴比（drat）。参照代码清单11-2，你可以对散点图矩阵中的这些变量重新排序并添加颜色。

代码清单11-2　gclus包生成的散点图矩阵

  1. library(gclus)
  2. mydata <- mtcars[c(1, 3, 5, 6)]
  3. mydata.corr <- abs(cor(mydata))
  5. mycolors <- dmat.color(mydata.corr)
  7. myorder <- order.single(mydata.corr)
  9. cpairs(mydata,
  10.        myorder,
  11.        panel.colors=mycolors,
  12.        gap=.5,
  13.        main="Variables Ordered and Colored by Correlation"
  14. )

代码清单11-2中使用的dmat.color()、order.single()和cpairs()函数都来自于gclus包。第一步，从mtcars数据框中选择所需的变量，并计算它们相关系数的绝对值。第二步，使用dmat.color()函数获取绘图的颜色。给定一个对称矩阵（本例中是相关系数矩阵），dmat.color()将返回一个颜色矩阵。第三步，可对图中变量进行排序。通过order.single()函数重排对象，可使得相似的对象更为靠近。本例中变量排序的基础是相关系数的相似性。最后，散点图矩阵将根据新的变量顺序（myorder）和颜色列表（mycolors）绘图、上色，gap选项使矩阵各单元格间的间距稍微增大一点。结果图形见图11-6。

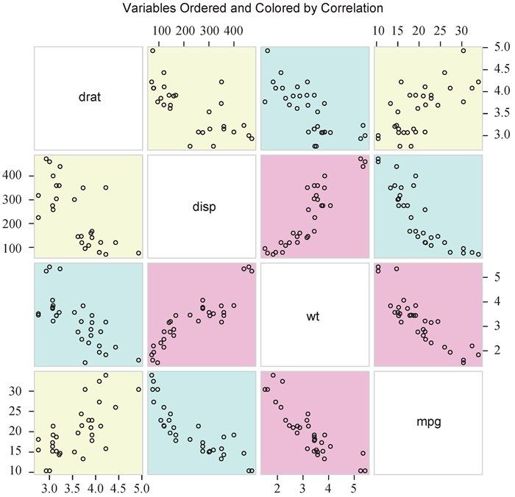
11.1　散点图 - 图6

图11-6　gclus包中的cpairs()函数生成的散点图矩阵。变量离主对角线越近，相关性越高

从图11-6中可以看到，相关性最高的变量对是车重与排量，以及每加仑英里数与车重（标了红色，并且离主对角线最近）。相关性最低的是后轴比与每加仑英里数（标了黄色，并且离主对角线很远）。当变量数众多，变量间的相关性变化很大时，该方法特别有用。在第16章，你还将会看到其他散点图矩阵的例子。

11.1.2　高密度散点图

当数据点重叠很严重时，用散点图来观察变量关系就显得“力不从心”了。下面是一个人为设计的例子，其中10 000个观测点分布在两个重叠的数据群中：

  1. set.seed(1234)
  3. n <- 10000
  4. c1 <- matrix(rnorm(n, mean=0, sd=.5), ncol=2)
  5. c2 <- matrix(rnorm(n, mean=3, sd=2), ncol=2)
  6. mydata <- rbind(c1, c2)
  7. mydata <- as.data.frame(mydata)
  8. names(mydata) <- c("x", "y")

若用下面的代码生成一幅标准的散点图：

  1. with(mydata,
  2.      plot(x, y, pch=19, main="Scatter Plot with 10,000 Observations"))

你将会得到如图11-7所示的图形。

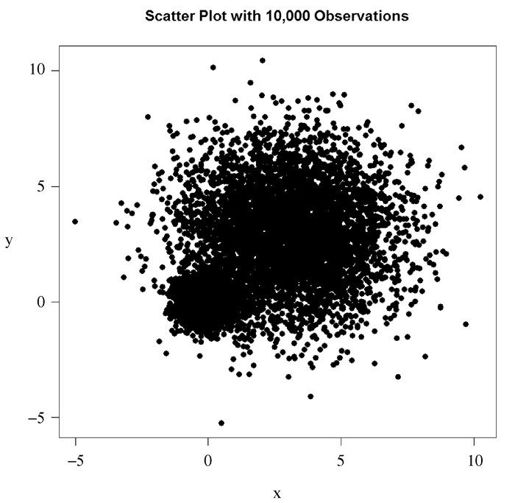
11.1　散点图 - 图7

图11-7　10 000个观测点的散点图，严重的重叠导致很难识别哪里数据点的密度最大

图11-7中，数据点的重叠导致识别x与y间的关系变得异常困难。针对这种情况，R提供了一些解决办法。你可以使用封箱、颜色和透明度来指明图中任意点上重叠点的数目。

smoothScatter()函数可利用核密度估计生成用颜色密度来表示点分布的散点图。代码如下：

  1. with(mydata,
  2.      smoothScatter(x, y, main="Scatterplot Colored by Smoothed Densities"))

生成图形见图11-8。

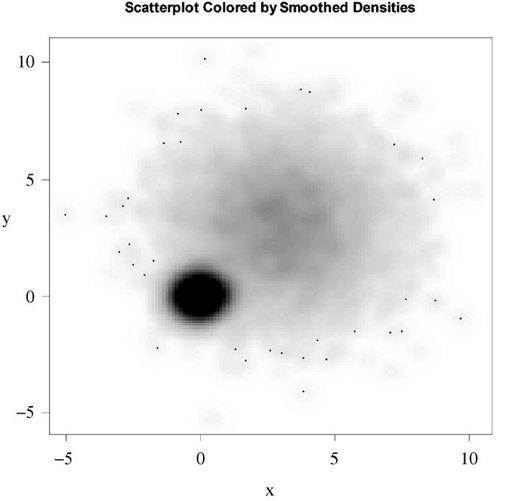
11.1　散点图 - 图8

图11-8　smoothScatter()利用光平滑密度估计绘制的散点图。此处密度易读性更强

与上面的方法不同，hexbin包中的hexbin()函数将二元变量的封箱放到六边形单元格中（图形比名称更直观）。示例如下：

  1. library(hexbin)
  2. with(mydata, {
  3.      bin <- hexbin(x, y, xbins=50)
  4.      plot(bin, main="Hexagonal Binning with 10,000 Observations")
  5.      })

你将得到如图11-9所示的散点图。

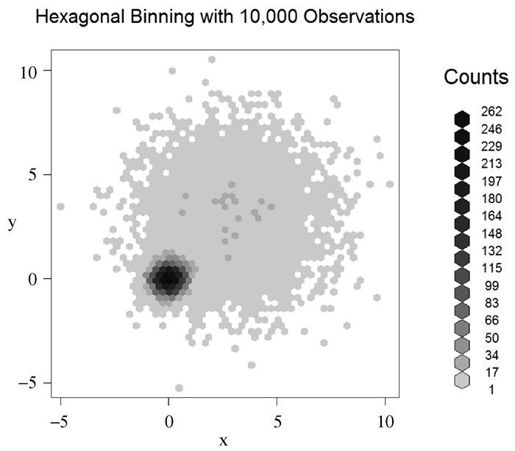
11.1　散点图 - 图9

图11-9　用六边形封箱图展示的各点上覆盖观测点数目的散点图。通过图例，数据的集中度很容易计算和观察

最后，IDPmisc包中的iplot()函数也可通过颜色来展示点的密度（在某特定点上数据点的数目）。代码如下：

  1. library(IDPmisc)
  2. with(mydata,
  3.      iplot(x, y, main="Image Scatter Plot with Color Indicating Density"))

生成图形见图11-10。

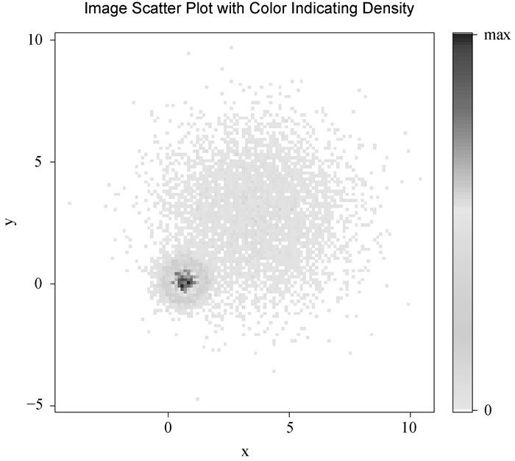
11.1　散点图 - 图10

图11-10　含10 000个观测的散点图，其中密度通过颜色标识。数据集中度很容易辨识

综上可见，基础包中的smoothScatter()函数，以及IDPmisc包中的ipairs()函数都可以对大数据集创建可读性较好的散点图矩阵。通过?smoothScatter和?ipairs可获得更多的示例。

11.1.3　三维散点图

散点图和散点图矩阵展示的都是二元变量关系。倘若你想一次对三个定量变量的交互关系进行可视化呢？本节例子中，你可以使用三维散点图。

例如，假使你对汽车英里数、车重和排量间的关系感兴趣，可用scatterplot3d中的scatterplot3d()函数来绘制它们的关系。格式如下：

  1. scatterplot3d(x, y, z)

x被绘制在水平轴上，y被绘制在竖直轴上，z被绘制在透视轴上。继续我们的例子：

  1. library(scatterplot3d)
  2. attach(mtcars)
  3. scatterplot3d(wt, disp, mpg,
  4.     main="Basic 3D Scatter Plot")

生成一幅三维散点图，见图11-11。

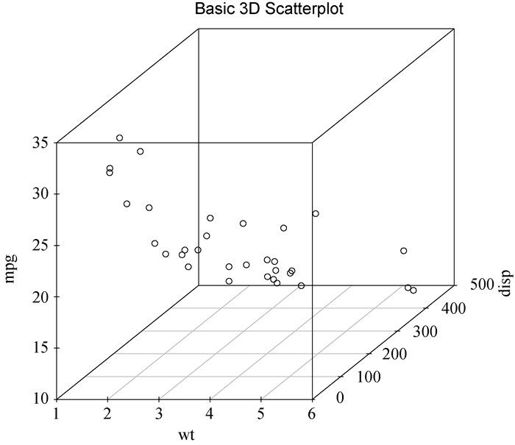
11.1　散点图 - 图11

图11-11　每加仑英里数、车重和排量的三维散点图

satterplot3d()函数提供了许多选项，包括设置图形符号、轴、颜色、线条、网格线、突出显示和角度等功能。例如代码：

  1. library(scatterplot3d)
  2. attach(mtcars)
  3. scatterplot3d(wt, disp, mpg,
  4.               pch=16,
  5.               highlight.3d=TRUE,
  6.               type="h",
  7.               main="3D Scatter Plot with Vertical Lines")

生成一幅突出显示效果的三维散点图，增强了纵深感，添加了连接点与水平面的垂直线（见图11-12）。

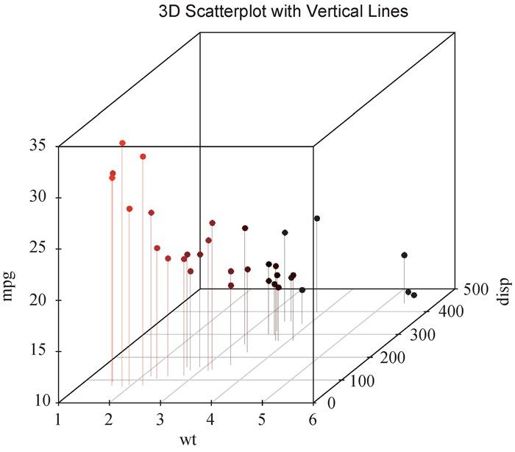
11.1　散点图 - 图12

图11-12　添加了垂直线和阴影的三维散点图（另见彩插图11-12）

作为最后一个例子，我们在刚才那幅图上添加一个回归面。所需代码为：

  1. library(scatterplot3d)
  2. attach(mtcars)
  3. s3d <-scatterplot3d(wt, disp, mpg,
  4.       pch=16,
  5.       highlight.3d=TRUE,
  6.       type="h",
  7.       main="3D Scatter Plot with Vertical Lines and Regression Plane")
  8. fit <- lm(mpg ~ wt+disp)
  9. s3d$plane3d(fit)

结果见图11-13。

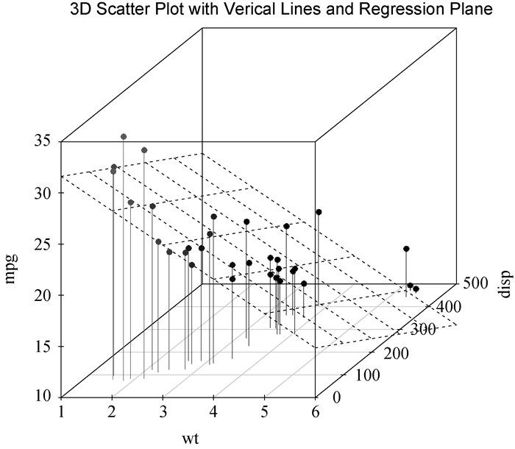
11.1　散点图 - 图13

图11-13　添加了垂直线、阴影和回归平面的三维散点图

图形利用多元回归方程，对通过车重和排量预测每加仑英里数进行了可视化处理。平面代表预测值，图中的点是实际值。平面到点的垂直距离表示残差值。若点在平面之上则表明它的预测值被低估了，而点在平面之下则表明它的预测值被高估了。多元回归内容见第8章。

旋转三维散点图

如果你能对三维散点图进行交互式操作，那么图形将会更好解释。R提供了一些旋转图形的功能，让你可以从多个角度观测绘制的数据点。

例如，你可用rgl包中的plot3d()函数创建可交互的三维散点图。你能通过鼠标对图形进行旋转。函数格式为：

  1. plot3d(x, y, z)

其中x、y和z是数值型向量，代表着各个点。你还可以添加如col和size这类的选项来分别控制点的颜色和大小。继续上面的例子，使用代码：

  1. library(rgl)
  2. attach(mtcars)
  3. plot3d(wt, disp, mpg, col="red", size=5)

你可获得如图11-14所示的图形。通过鼠标旋转坐标轴，你会发现三维散点图的旋转能使你更轻松地理解图形。

11.1　散点图 - 图14

图11-14　rgl包中的plot3d()函数生成的旋转三维散点图

你也可以使用Rcmdr包中类似的函数scatter3d()：

  1. library(Rcmdr)
  2. attach(mtcars)
  3. scatter3d(wt, disp, mpg)

结果图形见图11-15。

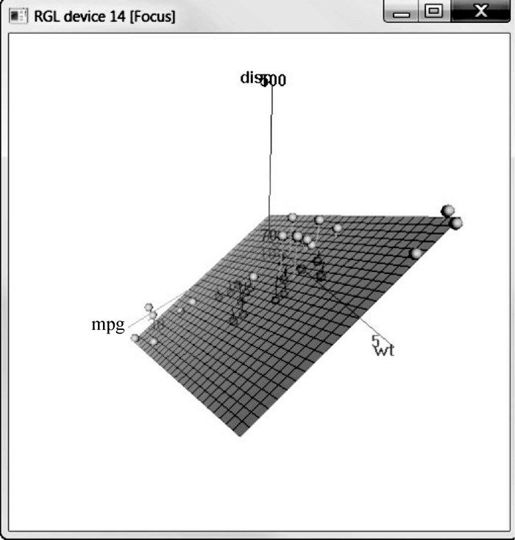
11.1　散点图 - 图15

图11-15　Rcmdr包中的scatter3d()生成的旋转三维散点图

scatter3d()函数可包含各种回归曲面，比如线性、二次、平滑和附加等类型。图形默认添加线性平面。另外，函数中还有可用于交互式识别点的选项。通过help(scatter3d)可获得函数的更多细节。在附录A中，我将对Rcmdr包做更详细的介绍。

11.1.4　气泡图

在之前的章节中，我们通过三维散点图来展示三个定量变量间的关系。现在介绍另外一种思路：先创建一个二维散点图，然后用点的大小来代表第三个变量的值。这便是气泡图（bubble plot）。

你可用symbols()函数来创建气泡图。该函数可以在指定的(x, y)坐标上绘制圆圈图、方形图、星形图、温度计图和箱线图。以绘制圆圈图为例：

  1. symbols(x, y, circle=radius)

其中x、y和radius是需要设定的向量，分别表示x、y坐标和圆圈半径。

你可能想用面积而不是半径来表示第三个变量，那么按照圆圈半径的公式（r = 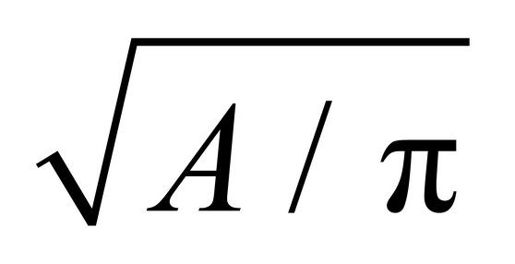11.1　散点图 - 图16）变换即可：

  1. symbols(x, y, circle=sqrt(z/pi))

z即第三个要绘制的变量。

现在我们把该方法应用到mtcars数据集上，x轴代表车重，y轴代表每加仑英里数，气泡大小代表发动机排量。代码如下：

  1. attach(mtcars)
  2. r <- sqrt(disp/pi)
  3. symbols(wt, mpg, circle=r, inches=0.30,
  4.         fg="white", bg="lightblue",
  5.         main="Bubble Plot with point size proportional to displacement",
  6.         ylab="Miles Per Gallon",
  7.         xlab="Weight of Car (lbs/1000)")
  8. text(wt, mpg, rownames(mtcars), cex=0.6)
  9. detach(mtcars)

生成图形见图11-16。选项inches是比例因子，控制着圆圈大小（默认最大圆圈为1英寸）。text()函数是可选函数，此处用来添加各个汽车的名称。从图中可以看到，随着每加仑汽油所行驶里程的增加，车重和发动机排量都逐渐减少。

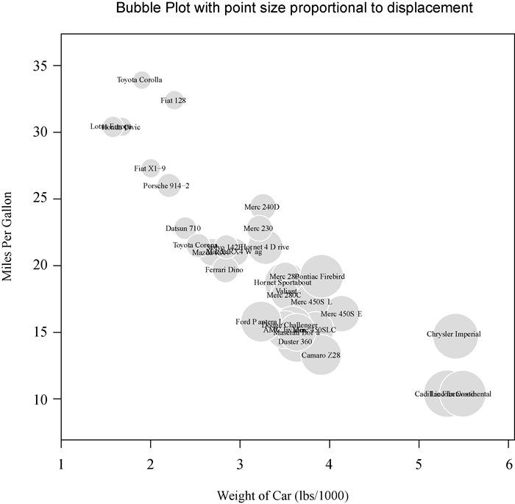
11.1　散点图 - 图17

图11-16　车重与每加仑英里数的气泡图，点大小与发动机排量成正比

一般来说，统计人员使用R时都倾向于避免用气泡图，原因和避免使用饼图一样：相比对长度的判断，人们对体积/面积的判断通常更困难。但是气泡图在商业应用中非常受欢迎，因此我还是将其包含在了本章里。

对于散点图，我已经介绍非常多了，之所以论述这么多的细节，主要是因为它在数据分析中占据着非常重要的位置。虽然散点图很简单，但是它们能帮你以最直接的方式展示数据，发现隐藏着的可能会被忽略的关系。