12.5　自助法

所谓自助法，即从初始样本重复随机替换抽样，生成一个或一系列待检验统计量的经验分布。无需假设一个特定的理论分布，便可生成统计量的置信区间，并能检验统计假设。

举一个例子便可非常清楚地阐释自助法的思路。比如，你想计算一个样本均值95%的置信区间。样本现有10个观测，均值为40，标准差为5。如果假设均值的样本分布为正态分布，那么（1-α/2）%的置信区间计算如下：

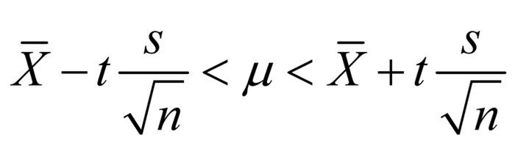
其中，t是自由度为n-1的t分布的1-α上界值。对于95%的置信区间，可得40 - 2.262(5/3.163) < μ < 40 + 2.262(5/3.162) 或者 36.424 < μ < 43.577。以这种方式创建的95%置信区间将会包含真实的总体均值。

倘若你假设均值的样本分布不是正态分布，该怎么办呢？可使用自助法。

• 从样本中随机选择10个观测，抽样后再放回。有些观测可能会被选择多次，有些可能一直都不会被选中。

• 计算并记录样本均值。

• 重复1和2一千次。

• 将1000个样本均值从小到大排序。

• 找出样本均值2.5%和97.5%的分位点。此时即初始位置和最末位置的第25个数，它们就限定了95%的置信区间。

本例中，样本均值很可能服从正态分布，自助法优势不太明显。但在其他许多案例中，自助法优势会十分明显。比如，你想估计样本中位数的置信区间，或者两样本中位数之差，该怎么做呢？正态理论没有现成的简单公式可套用，而自助法此时却是不错的选择。即使潜在分布未知，或出现了离群点，或者样本量过小，再或者是没有可供选择的参数方法，自助法将是生成置信区间和做假设检验的一个利器。