9.4　单因素协方差分析

单因素协方差分析（ANCOVA）扩展了单因素方差分析（ANOVA），包含一个或多个定量的协变量。下面的例子来自于multcomp包中的litter数据集（见Westfall et al.，1999）。怀孕小鼠被分为四个小组，每个小组接受不同剂量（0、5、50或500）的药物处理。产下幼崽的体重均值为因变量，怀孕时间为协变量。分析代码见代码清单9-3。

代码清单9-3　单因素ANCOVA

  1. > data(litter, package="multcomp")
  2. > attach(litter)
  3. > table(dose)
  4. dose
  5.   0   5  50 500
  6.  20  19  18  17
  7. > aggregate(weight, by=list(dose), FUN=mean)
  8.   Group.1    x
  9. 1       0 32.3
  10. 2       5 29.3
  11. 3      50 29.9
  12. 4     500 29.6
  13. > fit <- aov(weight ~ gesttime + dose)
  14. > summary(fit)
  15.             Df  Sum Sq Mean Sq F value   Pr(>F)
  16. gesttime     1  134.30  134.30  8.0493 0.005971 **
  17. dose         3  137.12   45.71  2.7394 0.049883 *
  18. Residuals   69 1151.27   16.69
  19. ---
  20. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

利用table()函数，可以看到每种剂量下所产的幼崽数并不相同：0剂量时（未用药）产崽20个，500剂量时产崽17个。再用aggregate()函数获得各组均值，可以发现未用药组幼崽体重均值最高（32.3）。ANCOVA的F检验表明：(a)怀孕时间与幼崽出生体重相关；(b)控制怀孕时间，药物剂量与出生体重相关。控制怀孕时间，确实发现每种药物剂量下幼崽出生体重均值不同。

由于使用了协变量，你可能想要获取调整的组均值——即去除协变量效应后的组均值。可使用effects包中的effects()函数来计算调整的均值：

  1. > library(effects)
  2. > effect("dose", fit)
  4.  dose effect
  5. dose
  6.    0    5   50  500
  7. 32.4 28.9 30.6 29.3

本例中，调整的均值与aggregate()函数得出的未调整的均值类似，但并非所有的情况都是如此。总之，effects包为复杂的研究设计提供了强大的计算调整均值的方法，并能将结果可视化，更多细节可参考CRAN上的文档。

和上一节的单因素ANOVA例子一样，剂量的F检验虽然表明了不同的处理方式幼崽的体重均值不同，但无法告知我们哪种处理方式与其他方式不同。同样，我们使用multcomp包来对所有均值进行成对比较。另外，multcomp包还可以用来检验用户自定义的均值假设。

假定你对未用药条件与其他三种用药条件影响是否不同感兴趣。代码清单9-4可以用来检验你的假设。

代码清单9-4　对用户定义的对照的多重比较

  1. > library(multcomp)
  2. > contrast <- rbind("no drug vs. drug" = c(3, -1, -1, -1))
  3. > summary(glht(fit, linfct=mcp(dose=contrast)))
  5. Multiple Comparisons of Means: User-defined Contrasts
  6. Fit: aov(formula = weight ~ gesttime + dose)
  8. Linear Hypotheses:
  9.                       Estimate Std. Error t value Pr(>|t|)
  10. no drug vs. drug == 0    8.284      3.209   2.581   0.0120 *
  11. ---
  12. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

对照c(3, -1, -1, -1)设定第一组和其他三组的均值进行比较。假设检验的t统计量（2.581）在p<0.05水平下显著，因此，可以得出未用药组比其他用药条件下的出生体重高的结论。其他对照可用rbind()函数添加（详见help(glht)）。

9.4.1　评估检验的假设条件

ANCOVA与ANOVA相同，都需要正态性和同方差性假设，可以用9.3.2节中相同的步骤来检验这些假设条件。另外，ANCOVA还假定回归斜率相同。本例中，假定四个处理组通过怀孕时间来预测出生体重的回归斜率都相同。ANCOVA模型包含怀孕时间*剂量的交互项时，可对回归斜率的同质性进行检验。交互效应若显著，则意味着时间和幼崽出生体重间的关系依赖于药物剂量的水平。代码和结果见代码清单9-5。

代码清单9-5　检验回归斜率的同质性

  1. > library(multcomp)
  2. > fit2 <- aov(weight ~ gesttime*dose, data=litter)
  3. > summary(fit2)
  4.               Df Sum Sq Mean Sq F value Pr(>F)
  5. gesttime       1    134     134    8.29 0.0054 **
  6. dose           3    137      46    2.82 0.0456 *
  7. gesttime:dose  3     82      27    1.68 0.1789
  8. Residuals     66   1069      16
  9. ---
  10. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

可以看到交互效应不显著，支持了斜率相等的假设。若假设不成立，可以尝试变换协变量或因变量，或使用能对每个斜率独立解释的模型，或使用不需要假设回归斜率同质性的非参数ANCOVA方法。sm包中的sm.ancova()函数为后者提供了一个例子。

9.4.2　结果可视化

HH包中的ancova()函数可以绘制因变量、协变量和因子之间的关系图。例如代码：

  1. > library(HH)
  2. > ancova(weight ~ gesttime + dose, data=litter)

生成的图形如图9-5所示。注意，为了适应黑白印刷，图形已经过修改。因此，你自己运行上面代码所得图形会略有不同。

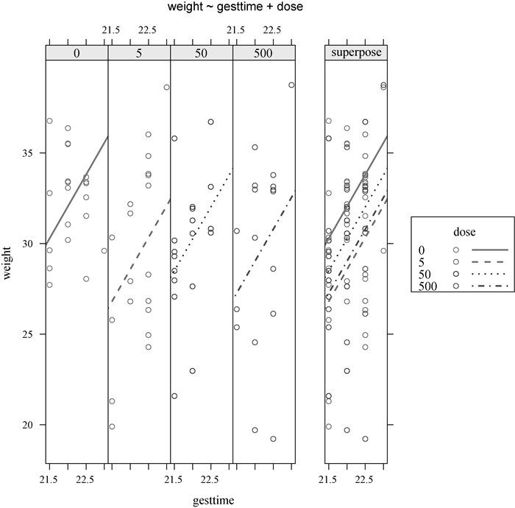
9.4　单因素协方差分析 - 图1

图9-5　四种药物处理组的怀孕时间和出生体重的关系图

从图中可以看到，用怀孕时间来预测出生体重的回归线相互平行，只是截距项不同。随着怀孕时间增加，幼崽出生体重也会增加。另外，还可以看到0剂量组截距项最大，5剂量组截距项最小。由于你上面的设置，直线会保持平行，若用ancova (weight ~ gettime*dose)，生成的图形将允许斜率和截距项依据组别而发生变化，这对可视化那些违背回归斜率同质性的实例非常有用。