14.5　小结

本章，我们主要学习了主成分分析（PCA）和探索性因子分析（EFA）两种方法。PCA在数据降维方面非常有用，它能用一组较少的不相关变量来替代大量相关变量，进而简化分析过程。EFA包含很多方法，可用来发现一组可观测变量背后潜在的或无法观测的结构（因子）。

与PCA综合数据和降低维度的目标不同，EFA是假设生成工具，它在帮助理解众多变量间的关系时非常有用，常用于社会科学的理论研究。

虽然两种方法表面上有许多相似之处，但也有重要的差异。本章中，我们探究了这两种方法的模型，学习了判断需提取的主成分/因子数的方法、提取主成分/因子和通过旋转增强解释力的方法，以及获得主成分/因子得分的技巧。图14-7总结了PCA和EFA的分析步骤。在本章最后，我们还简单介绍了R中其他可用的潜变量模型。

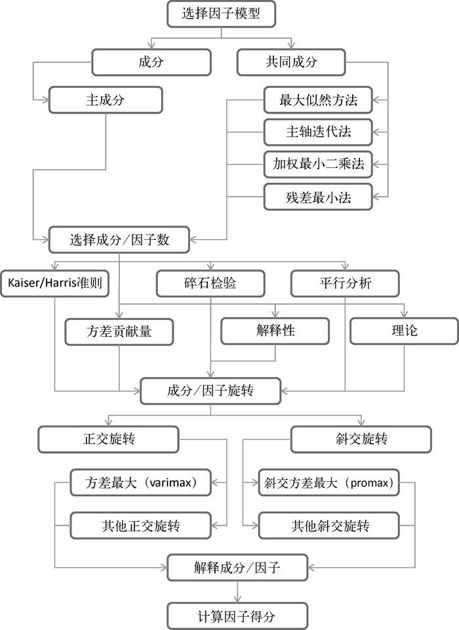
图14-7　主成分/探索性因子分析的分析步骤图

由于PCA和EFA都基于相关系数矩阵，因此在分析前去除缺失值显得非常重要。4.5节我们只是简略提到了处理缺失值的简单方法。在下一章中，我们将学习理解和处理缺失值的更完善的方法。