6.2　饼图

饼图在商业世界中无所不在，然而多数统计学家，包括相应R文档的编写者却都对它持否定态度。相对于饼图，他们更推荐使用条形图或点图，因为相对于面积，人们对长度的判断更精确。也许由于这个原因，R中饼图的选项与其他统计软件相比十分有限。

饼图可由以下函数创建：

  1. pie(x, labels)

其中x是一个非负数值向量，表示每个扇形的面积，而labels则是表示各扇形标签的字符型向量。代码清单6-5给出了四个示例，结果如图6-6所示。

代码清单6-5　饼图

  1. par(mfrow=c(2, 2))
  2. slices <- c(10, 12,4, 16, 8)         # ❶ 将四幅图形组合为一幅
  3. lbls <- c("US", "UK", "Australia", "Germany", "France")
  5. pie(slices, labels = lbls,
  6.     main="Simple Pie Chart")
  8. pct <- round(slices/sum(slices)*100)        # ❷ 为饼图添加比例数值
  9. lbls2 <- paste(lbls, " ", pct, "%", sep="")
  10. pie(slices, labels=lbls2, col=rainbow(length(lbls2)),
  11.     main="Pie Chart with Percentages")
  13. library(plotrix)
  14. pie3D(slices, labels=lbls,explode=0.1,
  15.       main="3D Pie Chart ")
  17. mytable <- table(state.region)        # ❸ 从表格创建饼图
  18. lbls3 <- paste(names(mytable), "\n", mytable, sep="")
  19. pie(mytable, labels = lbls3,
  20.     main="Pie Chart from a Table\n (with sample sizes)")

首先，你做了图形设置，这样四幅图形就会被组合为一幅❶。（多幅图形的组合在第3章中介绍过。）然后，你输入了前三幅图形将会使用的数据。

对于第二幅饼图❷，你将样本数转换为比例值，并将这项信息添加到了各扇形的标签上。如第3章所述，第二幅饼图使用rainbow()函数定义了各扇形的颜色。这里的rainbow(length(lbls2))将被解析为rainbow(5)，即为图形提供了五种颜色。

第三幅是使用plotrix包中的pie3D()函数创建的三维饼图。请在第一次使用之前先下载并安装这个包。如果说统计学家们只是不喜欢饼图的话，那么他们对三维饼图的态度就一定是唾弃了（即使他们私下感觉三维饼图好看）。这是因为三维效果无法增进对数据的理解，并且被认为是分散注意力的视觉花瓶。

第四幅图演示了如何从表格创建饼图❸。在本例中，你计算了美国不同地区的州数，并在绘制图形之前将此信息附加到了标签上。

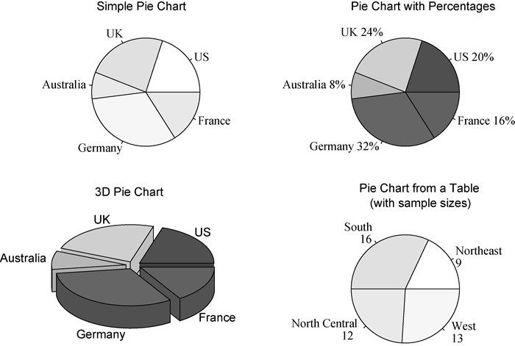
6.2　饼图 - 图1

图6-6　饼图示例

饼图让比较各扇形的值变得困难（除非这些值被附加在标签上）。例如，观察（第一幅）最简单的饼图，你能分辨出美国（US）和德国（Germany）的大小吗？（如果你可以，说明你的洞察力比我好。）为改善这种状况，我们创造了一种称为扇形图（fan plot）的饼图变种。扇形图（Lemon & Tyagi，2009）为用户提供了一种同时展示相对数量和相互差异的方法。在R中，扇形图是通过plotrix包中的fan.plot()函数实现的。

考虑以下代码和结果图（图6-7）：

  1. library(plotrix)
  2. slices <- c(10, 12,4, 16, 8)
  3. lbls <- c("US", "UK", "Australia", "Germany", "France")
  4. fan.plot(slices, labels = lbls, main="Fan Plot")

6.2　饼图 - 图2

图6-7　国别数据的扇形图

在一幅扇形图中，各个扇形相互叠加，并对半径做了修改，这样所有扇形就都是可见的。在这里可见德国对应的扇形是最大的，而美国的扇形大小约为其60%。法国的扇形大小似乎是德国的一半，是澳大利亚的两倍。请记住，在这里扇形的宽度（width）是重要的，而半径并不重要。

如你所见，确定扇形图中扇形的相对大小比饼图要简单得多。扇形图虽然尚未普及，但它仍然是新生力量。既然已经讲完了饼图和扇形图，就让我们转到直方图上吧。与条形图和饼图不同，直方图描述的是连续型变量的分布。