8.3　回归诊断

在上一节中，你使用lm()函数来拟合OLS回归模型，通过summary()函数获取模型参数和相关统计量。但是，没有任何输出告诉你模型是否合适，你对模型参数推断的信心依赖于它在多大程度上满足OLS模型统计假设。虽然在代码清单8-4中summary()函数对模型有了整体的描述，但是它没有提供关于模型在多大程度上满足统计假设的任何信息。

为什么这很重要？因为数据的无规律性或者错误设定了预测变量与响应变量的关系，都将致使你的模型产生巨大的偏差。一方面，你可能得出某个预测变量与响应变量无关的结论，但事实上，它们相关；另一方面，情况可能恰好相反。当你的模型应用到真实世界中时，预测效果可能很差，误差显著。

现在让我们通过confint()函数的输出来看看8.2.4节中states多元回归的问题。

> fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data=states)
> confint(fit)
                2.5 %   97.5 %
(Intercept) -6.55e+00 9.021318
Population   4.14e-05 0.000406
Illiteracy   2.38e+00 5.903874
Income      -1.31e-03 0.001441
Frost       -1.97e-02 0.020830

结果表明，文盲率改变1%，谋杀率就在95%的置信区间[2.38,5.90]中变化。另外，因为Frost的置信区间包含0，可以得出结论说，当其他变量不变时，温度的改变与谋杀率无关。不过，你对这些结果的信念，都只建立在你的数据满足统计假设的前提之上。

回归诊断技术向你提供了评价回归模型适用性的必要工具，它能帮助发现并纠正问题。首先，我们探讨使用R基础包中函数的标准方法，然后再看看car包中改进了的新方法。

8.3.1　标准方法

R基础安装中提供了大量检验回归分析中统计假设的方法。最常见的方法就是对lm()函数返回的对象使用plot()函数，可以生成评价模型拟合情况的四幅图形。下面是简单线性回归的例子：

fit <- lm(weight ~ height, data=women)
par(mfrow=c(2,2))
plot(fit)

生成图形见图8-6。par(mfrow = c(2, 2))将plot()函数绘制的四幅图形组合在一个大的2×2的图中。par()函数的介绍可参见第3章。

图8-6　体重对身高回归的诊断图

为理解这些图形，我们来回顾一下OLS回归的统计假设。

• 正态性　当预测变量值固定时，因变量成正态分布，则残差值也应该是一个均值为0的正态分布。正态Q-Q图（Normal Q-Q，右上）是在正态分布对应的值下，标准化残差的概率图。若满足正态假设，那么图上的点应该落在呈45度角的直线上；若不是如此，那么就违反了正态性的假设。

• 独立性　你无法从这些图中分辨出因变量值是否相互独立，只能从收集的数据中来验证。上面的例子中，没有任何先验的理由去相信一位女性的体重会影响另外一位女性的体重。假若你发现数据是从一个家庭抽样得来的，那么可能必须要调整模型独立性的假设。

• 线性　若因变量与自变量线性相关，那么残差值与预测（拟合）值就没有任何系统关联。换句话说，除了白噪声，模型应该包含数据中所有的系统方差。在“残差图与拟合图”（Residuals vs Fitted，左上）中可以清楚的看到一个曲线关系，这暗示着你可能需要对回归模型加上一个二次项。

• 同方差性　若满足不变方差假设，那么在位置尺度图（Scale-Location Graph，左下）中，水平线周围的点应该随机分布。该图似乎满足此假设。

最后一幅“残差与杠杆图”（Residuals vs Leverage，右下）提供了你可能关注的单个观测点的信息。从图形可以鉴别出离群点、高杠杆值点和强影响点。下面来详细介绍。

• 一个观测点是离群点，表明拟合回归模型对其预测效果不佳（产生了巨大的或正或负的残差）。

• 一个观测点有很高的杠杆值，表明它是一个异常的预测变量值的组合。也就是说，在预测变量空间中，它是一个离群点。因变量值不参与计算一个观测点的杠杆值。

• 一个观测点是强影响点（influential observation），表明它对模型参数的估计产生的影响过大，非常不成比例。强影响点可以通过Cook距离即Cook’s D统计量来鉴别。

不过老实说，我觉得残差—杠杆图的可读性差而且不够实用。在接下来的章节中，你将会看到对这一信息更好的呈现方法。

为了章节的完整性，让我们再看看二次拟合的诊断图。代码为：

fit2 <- lm(weight ~ height + I(height^2), data=women)
par(mfrow=c(2,2))
plot(fit2)

结果见图8-7。

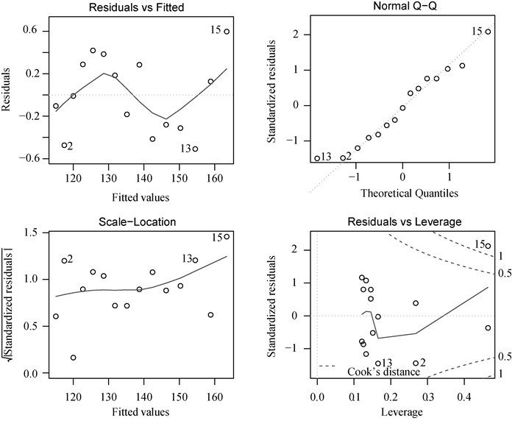
图8-7　体重对身高和身高平方的回归诊断图

这第二组图表明多项式回归拟合效果比较理想，基本符合了线性假设、残差正态性（除了观测点13）和同方差性（残差方差不变）。观测点15看起来像是强影响点（根据是它有较大的Cook距离值），删除它将会影响参数的估计。事实上，删除观测点13和15，模型会拟合得会更好。使用：

newfit <- lm(weight~ height + I(height^2), data=women[-c(13,15),])

即可拟合剔除点后的模型。但是对于删除数据，要非常小心，因为本应是你的模型去匹配数据，而不是反过来。

最后，我们再应用这个基本的方法，来看看states的多元回归问题。

fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data=states)
par(mfrow=c(2,2))
plot(fit)

结果展示在图8-8中。正如从图上看到的，除去Nevada一个离群点，模型假设得到了很好的满足。

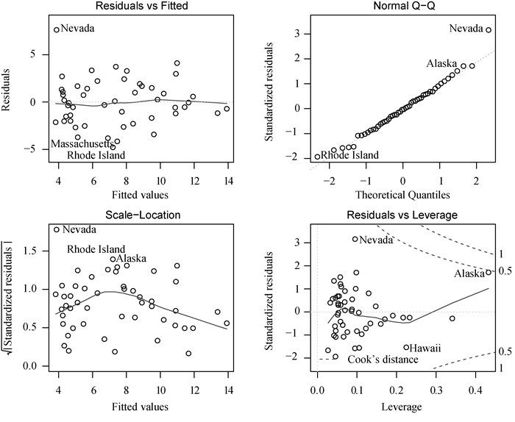
图8-8　谋杀率对州各因素的回归诊断图

虽然这些标准的诊断图形很有用，但是R中还有更好的工具可用，相比plot(fit)方法，我更推荐它们。

8.3.2　改进的方法

car包提供了大量函数，大大增强了拟合和评价回归模型的能力（参见表8-4）。 表8-4　（car包中的）回归诊断实用函数

值得注意的是，car包的2.x版本相对1.x版本作了许多改变，包括函数的名字和用法。本章基于2.x版本。

另外，gvlma包提供了对所有线性模型假设进行检验的方法。作为比较，我们将把它们应用到之前的多元回归例子中。

• 正态性

与基础包中的plot()函数相比，qqPlot()函数提供了更为精确的正态假设检验方法，它画出了在n-p-1个自由度的t分布下的学生化残差（studentized residual，也称学生化删除残差或折叠化残差）图形，其中n是样本大小，p是回归参数的数目（包括截距项）。代码如下：

library(car)
fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data=states)
qqPlot(fit, labels=row.names(states), id.method="identify",
  simulate=TRUE, main="Q-Q Plot")

qqPlot()函数生成的概率图见图8-9。id.method = "identify"选项能够交互式绘图—— 待图形绘制后，用鼠标单击图形内的点，将会标注函数中label选项的设定值。敲击Esc键，从图形下拉菜单中选择Stop，或者在图形上右击，都将关闭这种交互模式。此处，我已经鉴定出了Nevada异常。当simulate=TRUE时，95%的置信区间将会用参数自助法（自助法可参见第12章）生成。

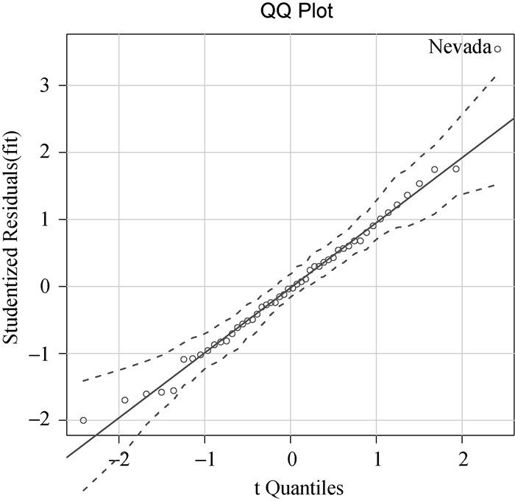
图8-9　学生化残差的Q-Q图

除了Nevada，所有的点都离直线很近，并都落在置信区间内，这表明正态性假设符合得很好。但是你也必须关注下Nevada，它有一个很大的正残差值（真实值—预测值），表明模型低估了该州的谋杀率。特别地：

> states["Nevada",]
　
       Murder Population Illiteracy Income Frost
Nevada   11.5        590        0.5   5149  188
　
> fitted(fit)["Nevada"]
　
  Nevada
3.878958
　
> residuals(fit)["Nevada"]
　
  Nevada
7.621042
　
> rstudent(fit)["Nevada"]
　
  Nevada
3.542929

可以看到，Nevada的谋杀率是11.5%，而模型预测的谋杀率为3.9%。

你应该会提出这样的问题：“为什么Nevada的谋杀率会比根据人口、收入、文盲率和温度预测所得的谋杀率高呢？”没有看过电影《盗亦有道》（Goodfellas）的你愿意猜一猜吗？

可视化误差还有其他方法，比如使用代码清单8-6中的代码。residplot()函数生成学生化残差柱状图（即直方图），并添加正态曲线、核密度曲线和轴须图。它不需要加载car包。

代码清单8-6　绘制学生化残差图的函数

residplot <- function(fit, nbreaks=10) {
               z <- rstudent(fit)
               hist(z, breaks=nbreaks, freq=FALSE,
               xlab="Studentized Residual",
               main="Distribution of Errors")
               rug(jitter(z), col="brown")
               curve(dnorm(x, mean=mean(z), sd=sd(z)),
                     add=TRUE, col="blue", lwd=2)
               lines(density(z)$x, density(z)$y,
                     col="red", lwd=2, lty=2)
               legend("topright",
                     legend = c( "Normal Curve", "Kernel Density Curve"),
                     lty=1:2, col=c("blue","red"), cex=.7)
          }
　
residplot(fit)

结果如图8-10所示。

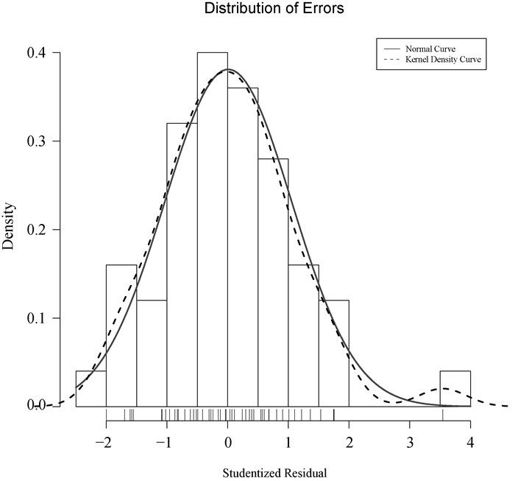
图8-10　用residplot()函数绘制的学生化残差分布图

正如你所看到的，除了一个很明显的离群点，误差很好地服从了正态分布。虽然Q-Q图已经蕴藏了很多信息，但我总觉得从一个柱状图或者密度图测量分布的斜度比使用概率图更容易。因此为何不一起使用这两幅图呢？

• 误差的独立性

之前章节提过，判断因变量值（或残差）是否相互独立，最好的方法是依据收集数据方式的先验知识。例如，时间序列数据通常呈现自相关性——相隔时间越近的观测相关性大于相隔越远的观测。car包提供了一个可做Durbin-Watson检验的函数，能够检测误差的序列相关性。在多元回归中，使用下面的代码可以做Durbin-Watson检验：

> durbinWatsonTest(fit)
 lag Autocorrelation D-W Statistic p-value
   1          -0.201          2.32   0.282
 Alternative hypothesis: rho != 0

p值不显著（p=0.282）说明无自相关性，误差项之间独立。滞后项（lag=1）表明数据集中每个数据都是与其后一个数据进行比较的。该检验适用于时间独立的数据，对于非聚集型的数据并不适用。注意，durbinWatsonTest()函数使用自助法（参见第12章）来导出p值，如果添加了选项simulate=FALSE，则每次运行测试时获得的结果都将略有不同。

• 线性

通过成分残差图（component plus residual plot）也称偏残差图（partial residual plot），你可以看看因变量与自变量之间是否呈非线性关系，也可以看看是否有不同于已设定线性模型的系统偏差，图形可用car包中的crPlots()函数绘制。

创建变量Xj的成分残差图，需要绘制点εi + (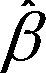j Xji) vs. Xji。其中残差项εi是基于所有模型的，i=1…n。每幅图都会给出(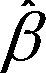j Xji) vs. Xji的直线。平滑拟合曲线（loess）将在第11章介绍。代码如下：

> library(car)
> crPlots(fit)

结果如图8-11所示。若图形存在非线性，则说明你可能对预测变量的函数形式建模不够充分，那么就需要添加一些曲线成分，比如多项式项，或对一个或多个变量进行变换（如用log(X)代替X），或用其他回归变体形式而不是线性回归。本章稍后会介绍变量变换。

从图8-11中可以看出，成分残差图证实了你的线性假设，线性模型形式对该数据集看似是合适的。

• 同方差性

car包提供了两个有用的函数，可以判断误差方差是否恒定。ncvTest()函数生成一个计分检验，零假设为误差方差不变，备择假设为误差方差随着拟合值水平的变化而变化。若检验显著，则说明存在异方差性（误差方差不恒定）。

spreadLevelPlot()函数创建一个添加了最佳拟合曲线的散点图，展示标准化残差绝对值与拟合值的关系。函数应用如代码清单8-7所示。

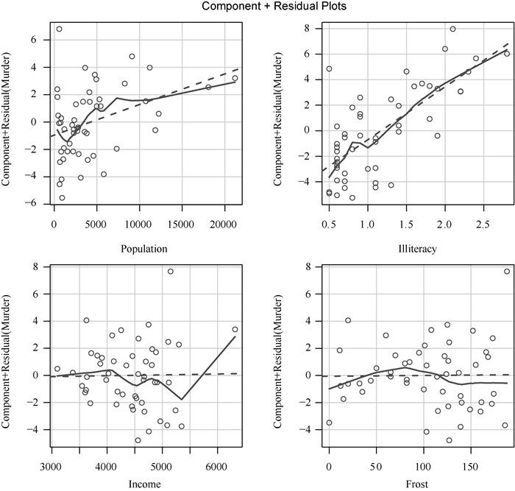
图8-11　谋杀率对州各因素回归的成分残差图

代码清单8-7　检验同方差性

> library(car)
> ncvTest(fit)
　
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare=1.7    Df=1     p=0.19
　
> spreadLevelPlot(fit)
　
Suggested power transformation:  1.2

可以看到，计分检验不显著（p=0.19），说明满足方差不变假设。你还可以通过分布水平图（图8-12）看到这一点，其中的点在水平的最佳拟合曲线周围呈水平随机分布。若违反了该假设，你将会看到一个非水平的曲线。代码结果建议幂次变换（suggested power transformation）的含义是，经过p次幂（Yp）变换，非恒定的误差方差将会平稳。例如，若图形显示出了非水平趋势，建议幂次转换为0.5，在回归等式中用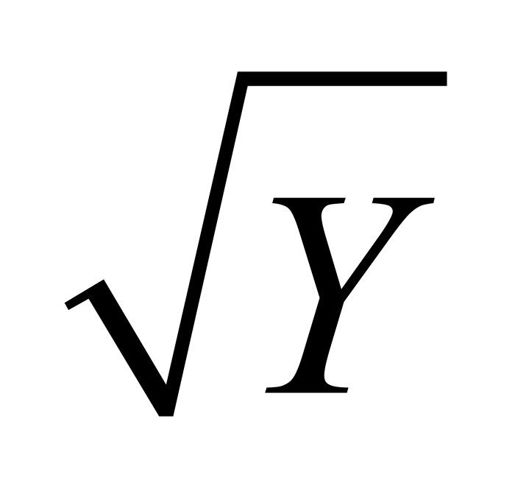代替Y，可能会使模型满足同方差性。若建议幂次为0，则使用对数变换。对于当前例子，异方差性很不明显，因此建议幂次接近1（不需要进行变换）。

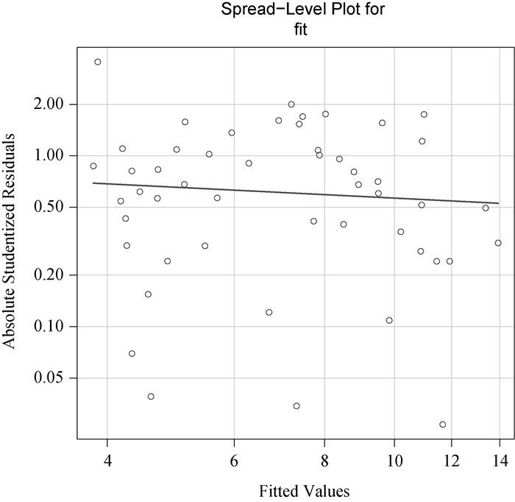
图8-12　评估不变方差的分布水平图

8.3.3　线性模型假设的综合验证

最后，让我一起学习下gvlma包中的gvlma()函数。gvlma()函数由Pena和Slate（2006）编写，能对线性模型假设进行综合验证，同时还能做偏斜度、峰度和异方差性的评价。换句话说，它给模型假设提供了一个单独的综合检验（通过/不通过）。代码清单8-8仍是对states数据的检验。

代码清单8-8　线性模型假设的综合检验

> library(gvlma)
> gvmodel <- gvlma(fit)
> summary(gvmodel)
ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS
USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
Level of Significance= 0.05
Call:
 gvlma(x=fit)
                   Value p-value                Decision
Global Stat        2.773   0.597 Assumptions acceptable.
Skewness           1.537   0.215 Assumptions acceptable.
Kurtosis           0.638   0.425 Assumptions acceptable.
Link Function      0.115   0.734 Assumptions acceptable.
Heteroscedasticity 0.482   0.487 Assumptions acceptable.

从输出项（Global Stat中的文字栏）我们可以看到数据满足OLS回归模型所有的统计假设（p=0.597）。若Decision下的文字表明违反了假设条件（比如p<0.05），你可以使用前几节讨论的方法来判断哪些假设没有被满足。

8.3.4　多重共线性

在即将结束回归诊断这一节前，让我们来看一个比较重要的问题，它与统计假设没有直接关联，但是对于解释多元回归的结果非常重要。

假设你正在进行一项握力研究，自变量包括DOB（Date Of Birth，出生日期）和年龄。你用握力对DOB和年龄进行回归，F检验显著，p<0.001。但是当你观察DOB和年龄的回归系数时，却发现它们都不显著（也就是说无法证明它们与握力相关）。到底发生了什么呢？

原因是DOB与年龄在四舍五入后相关性极大。回归系数测量的是当其他预测变量不变时，某个预测变量对响应变量的影响。那么此处就相当于假定年龄不变，然后测量握力与年龄的关系，这种问题就称作多重共线性（multicollinearity）。它会导致模型参数的置信区间过大，使单个系数解释起来很困难。

多重共线性可用统计量VIF（Variance Inflation Factor，方差膨胀因子）进行检测。VIF的平方根表示变量回归参数的置信区间能膨胀为与模型无关的预测变量的程度（因此而得名）。car包中的vif()函数提供VIF值。一般原则下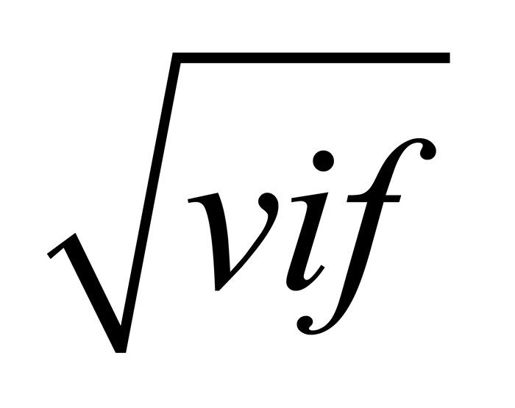，>2就表明存在多重共线性问题。代码参见代码清单8-9，结果表明预测变量不存在多重共线性问题。

代码清单8-9　检测多重共线性

>library(car)
> vif(fit)
Population Illiteracy     Income      Frost
       1.2        2.2        1.3        2.1
> sqrt(vif(fit)) > 2 # problem?
Population Illiteracy     Income      Frost
     FALSE      FALSE      FALSE      FALSE