11.3　相关图

相关系数矩阵是多元统计分析的一个基本方面。哪些被考察的变量与其他变量相关性很强，而哪些并不强？相关变量是否以某种特定的方式聚集在一起？随着变量数的增加，这类问题将变得更难回答。相关图作为一种相对现代的方法，可通过对相关系数矩阵的可视化来回答这些问题。

相关图非常容易解释，你只要看到它就会立马明白。以mtcars数据框中的变量相关性为例，它含有11个变量，对每个变量都测量了32辆汽车。利用下面的代码，你可以获得该数据的相关系数：

  1. > options(digits=2)
  2. > cor(mtcars)
  3.        mpg   cyl  disp    hp   drat    wt   qsec    vs     am  gear   carb
  4. mpg   1.00 -0.85 -0.85 -0.78  0.681 -0.87  0.419  0.66  0.600  0.48 -0.551
  5. cyl  -0.85  1.00  0.90  0.83 -0.700  0.78 -0.591 -0.81 -0.523 -0.49  0.527
  6. disp -0.85  0.90  1.00  0.79 -0.710  0.89 -0.434 -0.71 -0.591 -0.56  0.395
  7. hp   -0.78  0.83  0.79  1.00 -0.449  0.66 -0.708 -0.72 -0.243 -0.13  0.750
  8. drat  0.68 -0.70 -0.71 -0.45  1.000 -0.71  0.091  0.44  0.713  0.70 -0.091
  9. wt   -0.87  0.78  0.89  0.66 -0.712  1.00 -0.175 -0.55 -0.692 -0.58  0.428
  10. qsec  0.42 -0.59 -0.43 -0.71  0.091 -0.17  1.000  0.74 -0.230 -0.21 -0.656
  11. vs    0.66 -0.81 -0.71 -0.72  0.440 -0.55  0.745  1.00  0.168  0.21 -0.570
  12. am    0.60 -0.52 -0.59 -0.24  0.713 -0.69 -0.230  0.17  1.000  0.79  0.058
  13. gear  0.48 -0.49 -0.56 -0.13  0.700 -0.58 -0.213  0.21  0.794  1.00  0.274
  14. carb -0.55  0.53  0.39  0.75 -0.091  0.43 -0.656 -0.57  0.058  0.27  1.000

哪些变量相关性最强？哪些变量相对独立？是否存在某种聚集模式？如果不花点时间和精力（可能还需要用些彩笔做些注释），单利用这个相关系数矩阵来回答这些问题是比较困难的。

利用corrgram包中的corrgram()函数，你可以以图形方式展示该相关系数矩阵（见 图11-20）。代码为：

  1. library(corrgram)
  2. corrgram(mtcars, order=TRUE, lower.panel=panel.shade,
  3.          upper.panel=panel.pie, text.panel=panel.txt,
  4.          main="Correlogram of mtcars intercorrelations")

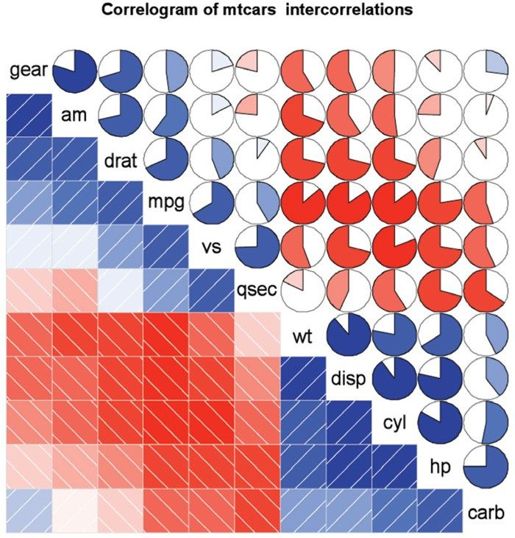
11.3　相关图 - 图1

图11-20　mtcars数据框中变量的相关系数图。矩阵行和列都通过主成分分析法进行了重新排序（另见彩插图11-20）

我们先从下三角单元格（在主对角线下方的单元格）开始解释这幅图形。默认地，蓝色和从左下指向右上的斜杠表示单元格中的两个变量呈正相关。反过来，红色和从左上指向右下的斜杠表示变量呈负相关。色彩越深，饱和度越高，说明变量相关性越大。相关性接近于0的单元格基本无色。本图为了将有相似相关模式的变量聚集在一起，对矩阵的行和列都重新进行了排序（使用主成分法）。

从图中含阴影的单元格中可以看到，gear、am、drat和mpg相互间呈正相关，wt、disp、hp和carb相互间也呈正相关。但第一组变量与第二组变量呈负相关。你还可以看到carb和am、vs和gear、vs和am以及drat和qsec四组变量间的相关性很弱。

上三角单元格用饼图展示了相同的信息。颜色的功能同上，但相关性大小由被填充的饼图块的大小来展示。正相关性将从12点钟处开始顺时针填充饼图，而负相关性则逆时针方向填充饼图。corrgram()函数的格式如下：

  1. corrgram(x, order=, panel=, text.panel=, diag.panel=)

其中，x是一行一个观测的数据框。当order = TRUE时，相关矩阵将使用主成分分析法对变量重排序，这将使得二元变量的关系模式更为明显。

选项panel设定非对角线面板使用的元素类型。你可以通过选项lower.panel和upper.panel来分别设置主对角线下方和上方的元素类型。而text.panel和diag.panel选项控制着主对角线元素类型。可用的panel值见表11-2。 表11-2　corrgram()函数的panel选项

位　　置 面板选项 描　　述
非对角线 panel.pie panel.shade panel.ellipse panel.pts 用饼图的填充比例来表示相关性大小用阴影的深度来表示相关性大小绘制置信椭圆和平滑拟合曲线绘制散点图
主对角线 panel.minmax panel.txt 输出变量的最大最小值输出的变量名字

让我们尝试第二个例子。代码如下：

  1. library(corrgram)
  2. corrgram(mtcars, order=TRUE, lower.panel=panel.ellipse,
  3.          upper.panel=panel.pts, text.panel=panel.txt,
  4.          diag.panel=panel.minmax,
  5.          main="Correlogram of mtcars data using scatter plots and ellipses")

生成的图形见图11-21。此处，我们在下三角区域使用平滑拟合曲线和置信椭圆，上三角区域使用散点图。

11.3　相关图 - 图2

图11-21　mtcars数据框中变量的相关系数图。下三角区域包含平滑拟合曲线和置信椭圆，上三角区域包含散点图。主对角面板包含变量最小和最大值。矩阵的行和列利用主成分分析法进行了重排序

为何散点图看起来怪怪的？

图11-21中绘制的散点图限制了一些变量的可用值。例如，挡位数须取3、4或5，气缸数须取4、6或者8。am（传动类型）和vs（V/S）都是二值型。因此上三角区域的散点图看起来很奇怪。

为数据选择合适的统计方法时，你一定要保持谨慎的心态。指定变量是有序因子还是无序因子可以为之提供有用的诊断。当R知道变量是类别型还是有序型时，它会使用适合于当前测量水平的统计方法。

最后，我们再看一个例子。代码如下：

  1. library(corrgram)
  2. corrgram(mtcars, lower.panel=panel.shade,
  3.          upper.panel=NULL, text.panel=panel.txt,
  4.          main="Car Mileage Data (unsorted)")

生成的图形见图11-22。此处，我们在下三角区域使用了阴影，并保持原变量顺序不变，上三角区域留白。

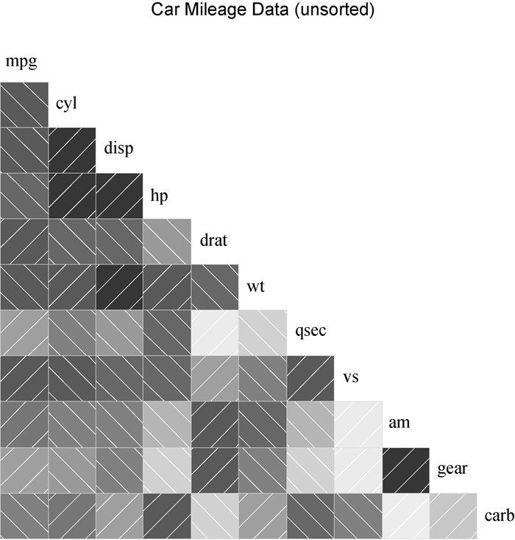
11.3　相关图 - 图3

图11-22　mtcars数据框中变量的相关系数图。下三角区域的阴影代表相关系数的大小和正负。变量按初始顺序排列

在继续下文之前，这里说明一下，你可自主控制corrgram()函数中使用的颜色。例如，你可在col.corrgram()函数中用colorRampPallette()函数来指定四种颜色：

  1. library(corrgram)
  2. col.corrgram <- function(ncol){
  3.                 colorRampPalette(c("darkgoldenrod4", "burlywood1",
  4.                                    "darkkhaki", "darkgreen"))(ncol)}
  5. corrgram(mtcars, order=TRUE, lower.panel=panel.shade,
  6.          upper.panel=panel.pie, text.panel=panel.txt,
  7.          main="A Corrgram (or Horse) of a Different Color")

运行下代码，看看所得的结果。

相关系数图是检验定量变量中众多二元关系的一种有效方式。由于图形相对比较新颖，因此教会目标读者看懂图形将是最大的挑战。

想了解相关图的更多内容，可参考Michael Friendly的文章“Corrgrams: Exploratory Displays for Correlation Matrices”（下载网址为http://www.math.yorku.ca/SCS/Papers/corrgram.pdf）。