13.3　泊松回归

当通过一系列连续型和/或类别型预测变量来预测计数型结果变量时，泊松回归是一个非常有用的工具。一个全面而易懂的泊松回归简介参见Coxe、West和Aiken的“The Analysis of Count Data: A Gentle Introduction to Poisson Regression and Its Alternatives”（2009）。

为阐述泊松回归模型的拟合过程，并探讨一些可能出现的问题，我们将使用robust包中的Breslow癫痫数据（Breslow，1993）。特别地，我们将讨论在治疗初期的八周内，抗癫痫药物对癫痫发病数的影响。继续下文前，请确定已安装robust包。

我们就遭受轻微或严重间歇性癫痫的病人的年龄和癫痫发病数收集了数据，包含病人被随机分配到药物组或者安慰剂组前八周和随机分配后八周两种情况。响应变量为sumY（随机化后八周内癫痫发病数），预测变量为治疗条件（Trt）、年龄（Age）和前八周内的基础癫痫发病数（Base）。之所以包含基础癫痫发病数和年龄，是因为它们对响应变量有潜在影响。在解释这些协变量后，我们感兴趣的是药物治疗是否能减少癫痫发病数。

首先，看看数据集的统计汇总信息：

  1. > data(breslow.dat, package="robust")
  2. > names(breslow.dat)
  3.  [1] "ID"    "Y1"    "Y2"    "Y3"    "Y4"    "Base"  "Age"   "Trt"   "Ysum"
  4. [10] "sumY"  "Age10" "Base4"
  6. > summary(breslow.dat[c(6,7,8,10)])
  7.       Base            Age              Trt          sumY
  8.  Min.   :  6.0   Min.   :18.0   placebo  :28   Min.   :  0.0
  9.  1st Qu.: 12.0   1st Qu.:23.0   progabide:31   1st Qu.: 11.5
  10.  Median : 22.0   Median :28.0                  Median : 16.0
  11.  Mean   : 31.2   Mean   :28.3                  Mean   : 33.1
  12.  3rd Qu.: 41.0   3rd Qu.:32.0                  3rd Qu.: 36.0
  13.  Max.   :151.0   Max.   :42.0                  Max.   :302.0

注意，虽然数据集有12个变量，但是我们只关注之前描述的四个变量。基础和随机化后的癫痫发病数都有很高的偏度。现在，我们更详细地考察响应变量。如下代码可生成的图形如图13-1所示。

  1. opar <- par(no.readonly=TRUE)
  2. par(mfrow=c(1,2))
  3. attach(breslow.dat)
  4. hist(sumY, breaks=20, xlab="Seizure Count",
  5.      main="Distribution of Seizures")
  6. boxplot(sumY ~ Trt, xlab=”Treatment", main=”Group Comparisons")
  7. par(opar)

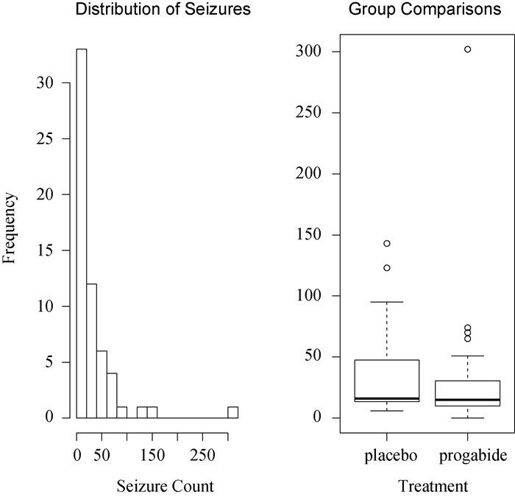
13.3　泊松回归 - 图1

图13-1　随机化后的癫痫发病数的分布情况（来源：Breslow癫痫数据）

从图13-1中可以清楚地看到因变量的偏倚特性以及可能的离群点。初看图形时，药物治疗下癫痫发病数似乎变小了，且方差也变小了（泊松分布中，较小的方差伴随着较小的均值）。与标准最小二乘回归不同，泊松回归并不关注方差异质性。

接下来拟合泊松回归：

  1. > fit <- glm(sumY ~ Base + Age + Trt, data=breslow.dat, family=poisson())
  2. > summary(fit)
  4. Call:
  5. glm(formula = sumY ~ Base + Age + Trt, family = poisson(), data = breslow.
  6.   dat)
  8. Deviance Residuals:
  9.    Min      1Q  Median      3Q     Max
  10. -6.057  -2.043  -0.940   0.793  11.006
  12. Coefficients:
  13.               Estimate Std. Error z value Pr(>|z|)
  14. (Intercept)   1.948826   0.135619   14.37  < 2e-16 ***
  15. Base          0.022652   0.000509   44.48  < 2e-16 ***
  16. Age           0.022740   0.004024    5.65  1.6e-08 ***
  17. Trtprogabide -0.152701   0.047805   -3.19   0.0014 **
  18. ---
  19. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  21. (Dispersion parameter for poisson family taken to be 1)
  23.     Null deviance: 2122.73  on 58  degrees of freedom
  24. Residual deviance:  559.44  on 55  degrees of freedom
  25. AIC: 850.7
  27. Number of Fisher Scoring iterations: 5

输出结果列出了偏差、回归参数、标准误和参数为0的检验。注意，此处预测变量在p<0.05的水平下都非常显著。

13.3.1　解释模型参数

使用coef()函数可获取模型系数，或者调用summary()函数的输出结果中的Coefficients表格：

  1. > coef(fit)
  2.  (Intercept)         Base          Age Trtprogabide
  3.       1.9488       0.0227       0.0227      -0.1527

在泊松回归中，因变量以条件均值的对数形式ln(λ)来建模。年龄的回归参数为0.0227，表明保持其他预测变量不变，年龄增加一岁，癫痫发病数的对数均值将相应增加0.03。截距项即当预测变量都为0时，癫痫发病数的对数均值。由于不可能为0岁，且调查对象的基础癫痫发病数均不为0，因此本例中截距项没有意义。

通常在因变量的初始尺度（癫痫发病数，而非发病数的对数）上解释回归系数比较容易。为此，指数化系数：

  1. > exp(coef(fit))
  2.  (Intercept)         Base          Age Trtprogabide
  3.        7.020        1.023        1.023        0.858

现在可以看到，保持其他变量不变，年龄增加一岁，期望的癫痫发病数将乘以1.023。这意味着年龄的增加与较高的癫痫发病数相关联。更为重要的是，一单位Trt的变化（即从安慰剂到治疗组），期望的癫痫发病数将乘以0.86，也就是说，保持基础癫痫发病数和年龄不变，服药组相对于安慰剂组癫痫发病数降低了20%。

另外需要牢记的是，与Logistic回归中的指数化参数相似，泊松模型中的指数化参数对响应变量的影响都是成倍增加的，而不是线性相加。同样，你还需要评价泊松模型的过度离势。

13.3.2　过度离势

泊松分布的方差和均值相等。当响应变量观测的方差比依据泊松分布预测的方差大时，泊松回归可能发生过度离势。由于处理计数型数据时经常发生过度离势，且过度离势会对结果的可解释性造成负面影响，因此我们需要花些时间讨论该问题。

可能发生过度离势的原因有如下几个（Coxe et al.，2009）。

  • 遗漏了某个重要的预测变量。

  • 可能因为事件相关。在泊松分布的观测中，计数中每次事件都被认为是独立发生的。以癫痫数据为例，这意味着对于任何病人，每次癫痫发病的概率与其他癫痫发病的概率相互独立。但是这个假设通常都无法满足。对于某个的病人，在已知他已经发生了39次癫痫时，第一次发生癫痫的概率不可能与第40次发生癫痫的概率相同。

  • 在纵向数据分析中，重复测量的数据由于内在群聚特性可导致过度离势。此处并不讨论纵向泊松模型。

如果存在过度离势，在模型中你无法进行解释，那么可能会得到很小的标准误和置信区间，并且显著性检验也过于宽松（也就是说，你将会发现并不真实存在的效应）。

与Logistic回归类似，此处如果残差偏差与残差自由度的比例远远大于1，那么表明存在过度离势。对于癫痫数据，它的比例为：

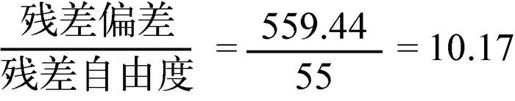
13.3　泊松回归 - 图2

很显然，比例远远大于1。

qcc包提供了一个对泊松模型过度离势的检验方法。（在首次使用前，请确保已经下载和安装此包。）如下代码可进行癫痫数据过度离势的检验：

  1. > library(qcc)
  2. > qcc.overdispersion.test(breslow.dat$sumY, type="poisson")
  4. Overdispersion test Obs.Var/Theor.Var Statistic p-value
  5.        poisson data              62.9      3646       0

意料之中，显著性检验的p值果然小于0.05，进一步表明确实存在过度离势。

通过用family = "quasipoisson"替换family = "poisson"， 你仍然可以使用glm()函数对该数据进行拟合。这与Logistic回归处理过度离势的方法是相同的。

  1. > fit.od <- glm(sumY ~ Base + Age + Trt, data=breslow.dat,
  2.                 family=quasipoisson())
  3. > summary(fit.od)
  5. Call:
  6. glm(formula = sumY ~ Base + Age + Trt, family = quasipoisson(),
  7.     data = breslow.dat)
  9. Deviance Residuals:
  10.    Min      1Q  Median      3Q     Max
  11. -6.057  -2.043  -0.940   0.793  11.006
  13. Coefficients:
  14.              Estimate Std. Error t value Pr(>|t|)
  15. (Intercept)   1.94883    0.46509    4.19  0.00010 ***
  16. Base          0.02265    0.00175   12.97  < 2e-16 ***
  17. Age           0.02274    0.01380    1.65  0.10509
  18. Trtprogabide -0.15270    0.16394   -0.93  0.35570
  19. ---
  20. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  22. (Dispersion parameter for quasipoisson family taken to be 11.8)
  24.     Null deviance: 2122.73  on 58  degrees of freedom
  25. Residual deviance:  559.44  on 55  degrees of freedom
  26. AIC: NA
  28. Number of Fisher Scoring iterations: 5

注意，使用类泊松（quasi-Poisson）方法所得的参数估计与泊松方法相同，但标准误变大了许多。此处，标准误越大将会导致Trt（和Age）的p值越大于0.05。当考虑过度离势，并控制基础癫痫数和年龄时，并没有充足的证据表明药物治疗相对于使用安慰剂能显著降低癫痫发病次数。

不过请记住，本例只是用于阐释泊松模型，它的结果并不能用来反映真实世界中的普罗加比（治疗癫痫）的药效问题。我不是医生（至少不是一个药剂师），也未在电视中扮演过这类角色，数据只是用来阐释模型的。

最后，我们以探究泊松回归的一些重要变种和扩展结束本节。

13.3.3　扩展

R提供了基本泊松回归模型的一些有用扩展，包括允许时间段变化、存在过多0时会自动修正的模型，以及当数据存在离群点和强影响点时有用的稳健模型。下面分别对它们进行介绍。

  • 时间段变化的泊松回归

对于泊松回归的讨论，我们一直将响应变量局限在一个固定长度时间段中进行测量（例如，八周内的癫痫发病数、过去一年内交通事故数、一天中亲近社会的举动次数），整个观测集中时间长度都是不变的。不过，你也可以拟合允许时间段变化的泊松回归模型。此处假设结果变量是一个比率。

为分析比率，必须包含一个记录每个观测的时间长度的变量（如time）。然后，将模型从：

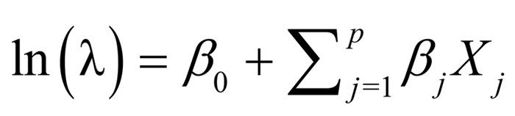
13.3　泊松回归 - 图3

修改为：

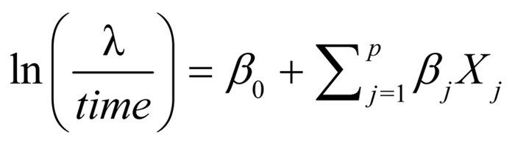
13.3　泊松回归 - 图4

或等价的：

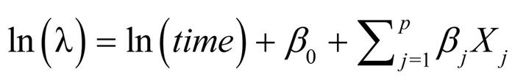
13.3　泊松回归 - 图5

为拟合新模型，你需要使用glm()函数中的offset选项。例如在Breslow癫痫研究中，假设病人随机分组后检测的时间长度在14天到60天间变化。你可以将癫痫发病率作为因变量（假设已记录了每个病人发病的时间），然后拟合模型：

  1. fit <- glm(sumY ~ Base + Age + Trt, data=breslow.dat,
  2.            offset= log(time), family=poisson())

其中sumY指随机化分组后在每个病人被研究期间其癫痫发病的次数。此处假定比率不随时间变化（比如，4天中发生2次癫痫与20天发生10次癫痫比率相同）。

  • 零膨胀的泊松回归

在一个数据集中，0计数的数目时常比用泊松模型预测的数目多。当总体的一个子群体无任何被计数的行为时，就可能发生这种问题。以Logistic回归中的婚外情数据为例，初始结果变量（affairs）记录了调查对象在过去一年中的婚外偷腥次数。在整个调查期间，很有可能有一群对配偶忠诚的群体从未有过婚外情。这便称为结构零值（相对于调查中那群有婚外情的人）。

此时，你可以使用零膨胀的泊松回归（zero-inflated Poisson regression）分析该数据。它将同时拟合两个模型：一个用来预测哪些人又会发生婚外情，另外一个用来预测排除了婚姻忠诚者后的调查对象会发生多少次婚外情。你可以把该模型看做Logistic回归（预测结构零值）和泊松回归（预测无结构零值观测的计数）的组合。pscl包中的zeroinfl()函数可做零膨胀泊松回归。

  • 稳健泊松回归

robust包中的glmRob()函数可以拟合稳健广义线性模型，包含稳健泊松回归。正如上文所提到的，当存在离群点和强影响点时，该方法会很有效。

深入探究

广义线性模型是一种数学上的复杂模型，有许多可用的学习资源。Dunteman和Ho的An Introduction to Generalized Linear Models（2006）是一个较好的简介，可供参考；McCullagh和Nelder的Generalized Linear Models, Second Edition（1989）则是经典的广义线性模型的（高级）材料。Dobson和Barnett的An Introduction to Generalized Linear Models, Third Edition（2008）和Fox的Applied Regression Analysis and Generalized Linear Models（2008）给出了一个全面而易懂的讲义，另外还有以R为背景的优秀简介可参考：Faraway (2006)和Fox (2002)。