13.1　广义线性模型和glm()函数

许多广泛应用的、流行的数据分析方法其实都归属于广义线性模型框架。本节中，我们将简短回顾这些方法背后的理论。你可跳过本节，稍后再回头阅读，这对于模型理解没有太大影响。

现假设你想要对响应变量Y和 p个预测变量X₁…X_p间的关系进行建模。在标准线性模型中，你可以假设Y呈正态分布，关系的形式为：

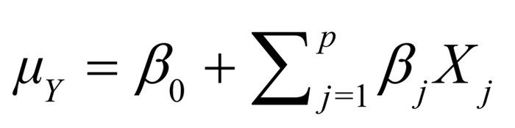
该等式表明响应变量的条件均值是预测变量的线性组合。参数β_j指一单位X_j的变化造成的Y预期的变化，β₀指当所有预测变量都为0时Y的预期值。对于该等式，你可通俗地理解为：给定一系列X变量的值，赋予X变量合适的权重，然后将它们加起来，便可预测Y观测值分布的均值。

值得注意的是，你并没有对预测变量X_j做任何分布的假设，与Y不同，它们不需要呈正态分布。实际上，它们常为类别型变量（比如方差分析设计）。另外，对预测变量使用非线性函数也是允许的，比如你常会使用预测变量X²或者X₁ × X₂，只要等式的参数（β₀,β₁,…，β_p）为线性即可。

广义线性模型拟合的形式为：

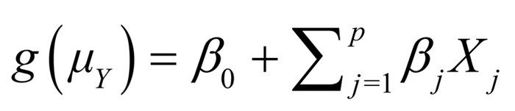
其中g(μ_Y)是条件均值的函数（称为连接函数）。另外，你可放松Y为正态分布的假设，改为Y服从指数分布族中的一种分布即可。设定好连接函数和概率分布后，便可以通过最大似然估计的多次迭代推导出各参数值。

13.1.1　glm()函数

R中可通过glm函数（还可用其他专门的函数）拟合广义线性模型。它的形式与lm()类似，只是多了一些参数。函数的基本形式为：

glm(formula, family=family(link=function), data=)

表13-1列出了概率分布（family）和相应默认的连接函数（function）。

表13-1　glm()的参数

glm()函数可以拟合许多流行的模型，比如Logistic回归、泊松回归和生存分析（此处不考虑）。下面对前两个模型进行阐述。假设你有一个响应变量（Y）、三个预测变量（X1、X2、X3）和一个包含数据的数据框（mydata）。

Logistic回归适用于二值响应变量（0,1）。模型假设Y服从二项分布，线性模型的拟合形式为：

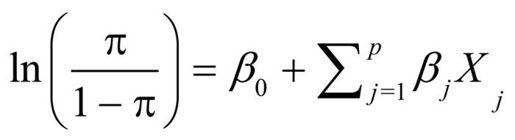
其中π= μ_Y是Y的条件均值（即给定一系列X的值时Y = 1的概率），(π/1-π)为Y = 1 时的优势比，log(π/1-π)为对数优势比，或logit。本例中，log(π/1-π)为连接函数，概率分布为二项分布，可用如下代码拟合Logistic回归模型：

glm(Y~X1+X2+X3, family=binomial(link="logit"), data=mydata)

Logistic回归在13.2节有更详细的介绍。

泊松回归适用于在给定时间内响应变量为事件发生数目的情形。它假设Y服从泊松分布，线性模型的拟合形式为：

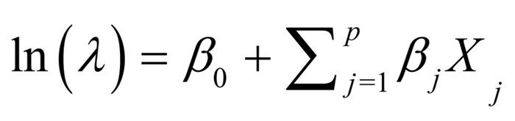
其中λ是Y的均值（也等于方差）。此时，连接函数为log(λ)，概率分布为泊松分布，可用如下代码拟合泊松回归模型：

glm(Y~X1+X2+X3, family=poisson(link="log"), data=mydata)

泊松回归在13.3节有介绍。

值得注意的是，标准线性模型也是广义线性模型的一个特例。如果令连接函数g( μ_Y) = μ_Y 或恒等函数，并设定概率分布为正态（高斯）分布，那么：

glm(Y~X1+X2+X3, family=gaussian(link="identity"), data=mydata)

生成的结果与下列代码的结果相同：

lm(Y~X1+X2+X3, data=mydata)

总之，广义线性模型通过拟合响应变量的条件均值的一个函数（不是响应变量的条件均值），假设响应变量服从指数分布族中的某个分布（并不仅限于正态分布），极大地扩展了标准线性模型。模型参数估计的推导依据的是极大似然估计，而非最小二乘法。

13.1.2　连用的函数

与分析标准线性模型时lm()连用的许多函数在glm()中都有对应的形式，其中一些常见的函数见表13-2。 表13-2　与glm()连用的函数

我们将在后面章节讲解这些函数的示例，在下一节中，我们将简要介绍模型适用性的评价。

13.1.3　模型拟合和回归诊断

与标准（OLS）线性模型一样，模型适用性的评价对于广义线性模型也非常重要。但遗憾的是，对于标准的评价过程，统计圈子仍莫衷一是。一般来说，你可以使用第8章中描述的方法，但要牢记以下建议。

当评价模型的适用性时，你可以绘制初始响应变量的预测值与残差的图形。例如，如下代码可绘制一个常见的诊断图：

plot(predict(model, type="response"),
    residuals(model, type= "deviance"))

其中，model为glm()函数返回的对象。

R将列出帽子值（hat value）、学生化残差值和Cook距离统计量的近似值。不过，对于识别异常点的阈值，现在并没统一答案，它们都是通过相互比较来进行判断。其中一个方法就是绘制各统计量的参考图，然后找出异常大的值。例如，如下代码可创建三幅诊断图：

plot(hatvalues(model))
plot(rstudent(model))
plot(cooks.distance(model))

你还可以用其他方法，代码如下：

library(car)
influencePlot(model)

它可以创建一个综合性的诊断图。在后面的图形中，横轴代表杠杆值，纵轴代表学生化残差值，而绘制的符号大小与Cook距离大小成正比。

当响应变量有许多值时，诊断图非常有用；而当响应变量只有有限个值时（比如Logistic回归），诊断图的功效就会降低很多。

若想更深入了解广义线性模型的回归诊断，可参考Fox（2008）和Faraway（2006）。本章后面几节将详细介绍两个最流行的广义线性模型：Logistic回归和泊松回归。