14.3　探索性因子分析

EFA的目标是通过发掘隐藏在数据下的一组较少的、更为基本的无法观测的变量，来解释一组可观测变量的相关性。这些虚拟的、无法观测的变量称作因子。（每个因子被认为可解释多个观测变量间共有的方差，因此准确来说，它们应该称作公共因子。）

模型的形式为：

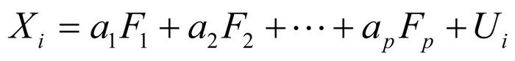
14.3　探索性因子分析 - 图1

其中Xi是第i个可观测变量（i = 1…k），Fj是公共因子（j = 1…p），并且p<k。Ui是Xi变量独有的部分（无法被公共因子解释）。ai可认为是每个因子对复合而成的可观测变量的贡献值。回到本章开头的Harman74.cor的例子，我们认为每个个体在24个心理学测验上的观测得分，是根据四个潜在心理学因素的加权能力值组合而成。

虽然PCA和EFA存在差异，但是它们的许多分析步骤都是相似的。为阐述EFA的分析过程，我们用它来对六个心理学测验间的相关性进行分析。112个人参与了六个测验，包括非语言的普通智力测验（general）、画图测验（picture）、积木图案测验（blocks）、迷津测验（maze）、阅读测验（reading）和词汇测验（vocab）。我们如何用一组较少的、潜在的心理学因素来解释参与者的测验得分呢？

数据集ability.cov提供了变量的协方差矩阵，你可用cov2cor()函数将其转化为相关系数矩阵。数据集没有缺失值。

  1. > options(digits=2)
  2. > covariances <- ability.cov$cov
  3. > correlations <- cov2cor(covariances)
  4. > correlations
  5.         general picture blocks maze reading vocab
  6. general    1.00    0.47   0.55 0.34    0.58  0.51
  7. picture    0.47    1.00   0.57 0.19    0.26  0.24
  8. blocks     0.55    0.57   1.00 0.45    0.35  0.36
  9. maze       0.34    0.19   0.45 1.00    0.18  0.22
  10. reading    0.58    0.26   0.35 0.18    1.00  0.79
  11. vocab      0.51    0.24   0.36 0.22    0.79  1.00

因为要寻求用来解释数据的潜在结构，可使用EFA方法。与使用PCA相同，下一步工作为判断需要提取几个因子。

14.3.1　判断需提取的公共因子数

用fa.parallel()函数可判断需提取的因子数：

  1. > library(psych)
  2. > covariances <- ability.cov$cov
  3. > correlations <- cov2cor(covariances)
  4. > fa.parallel(correlations, n.obs=112, fa="both", n.iter=100,
  5.               main="Scree plots with parallel analysis")

结果见图14-4。注意，代码中使用了fa = "both"，因子图形将会同时展示主成分和公共因子分析的结果。

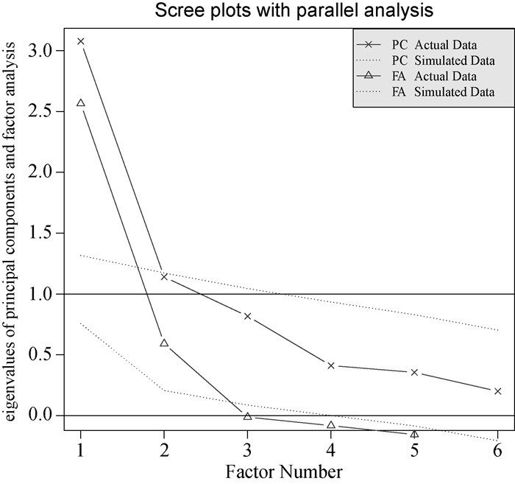
14.3　探索性因子分析 - 图2

图14-4　判断心理学测验需要保留的因子数。图中同时展示了PCA和EFA的结果。PCA结果建议提取一个或者两个成分，EFA建议提取两个因子

图形中有几个值得注意的地方。如果使用PCA方法，你可能会选择一个成分（碎石检验和平行分析）或者两个成分（特征值大于1）。当摇摆不定时，高估因子数通常比低估因子数的结果好，因为高估因子数一般较少曲解“真实”情况。

观察EFA的结果，显然需提取两个因子。碎石检验的前两个特征值（三角形）都在拐角处之上，并且大于基于100次模拟数据矩阵的特征值均值。对于EFA，Kaiser-Harris准则的特征值数大于0，而不是1。（大部分人都没有意识到这一点。）图形中该准则也建议选择两个因子。

14.3.2　提取公共因子

现在你决定提取两个因子，可以使用fa()函数获得相应的结果。fa()函数的格式如下：

  1. fa(r, nfactors=, n.obs=, rotate=, scores=, fm=)

其中：

  • r是相关系数矩阵或者原始数据矩阵；

  • nfactors设定提取的因子数（默认为1）；

  • n.obs是观测数（输入相关系数矩阵时需要填写）；

  • rotate设定旋转的方法（默认互变异数最小法）；

  • scores设定是否计算因子得分（默认不计算）；

  • fm设定因子化方法（默认极小残差法）。

与PCA不同，提取公共因子的方法很多，包括最大似然法（ml）、主轴迭代法（pa）、加权最小二乘法（wls）、广义加权最小二乘法（gls）和最小残差法（minres）。统计学家青睐使用最大似然法，因为它有良好的统计性质。不过有时候最大似然法不会收敛，此时使用主轴迭代法效果会很好。欲了解更多提取公共因子的方法，可参阅Mulaik（2009）和Corsuch（1983）。

本例使用主轴迭代法（fm = "pa"）提取未旋转的因子。结果见代码清单14-6。

代码清单14-6　未旋转的主轴迭代因子法

  1. > fa <- fa(correlations, nfactors=2, rotate="none", fm="pa")
  2. > fa
  3. Factor Analysis using method =  pa
  4. Call: fa(r = correlations, nfactors = 2, rotate = "none", fm = "pa")
  5. Standardized loadings based upon correlation matrix
  6.          PA1   PA2   h2   u2
  7. general 0.75  0.07 0.57 0.43
  8. picture 0.52  0.32 0.38 0.62
  9. blocks  0.75  0.52 0.83 0.17
  10. maze    0.39  0.22 0.20 0.80
  11. reading 0.81 -0.51 0.91 0.09
  12. vocab   0.73 -0.39 0.69 0.31
  14.                 PA1  PA2
  15. SS loadings    2.75 0.83
  16. Proportion Var 0.46 0.14
  17. Cumulative Var 0.46 0.60
  18. [……已删除额外输出……]

可以看到，两个因子解释了六个心理学测验60%的方差。不过因子载荷阵的意义并不太好解释，此时使用因子旋转将有助于因子的解释。

14.3.3　因子旋转

你可以使用正交旋转或者斜交旋转来旋转14.3.4节中两个因子的结果。现在我们同时尝试下两种方法，看看它们的异同。首先使用正交旋转（见代码清单14-7）。

代码清单14-7　用正交旋转提取因子

  1. > fa.varimax <- fa(correlations, nfactors=2, rotate="varimax", fm="pa")
  2. > fa.varimax
  3. Factor Analysis using method =  pa
  4. Call: fa(r = correlations, nfactors = 2, rotate = "varimax", fm = "pa")
  5. Standardized loadings based upon correlation matrix
  6.          PA1  PA2   h2   u2
  7. general 0.49 0.57 0.57 0.43
  8. picture 0.16 0.59 0.38 0.62
  9. blocks  0.18 0.89 0.83 0.17
  10. maze    0.13 0.43 0.20 0.80
  11. reading 0.93 0.20 0.91 0.09
  12. vocab   0.80 0.23 0.69 0.31
  14.                 PA1  PA2
  15. SS loadings    1.83 1.75
  16. Proportion Var 0.30 0.29
  17. Cumulative Var 0.30 0.60
  19. [……已删除额外输出……]

结果显示因子变得更好解释了。阅读和词汇在第一因子上载荷较大，画图、积木图案和迷宫在第二因子上载荷较大，非语言的普通智力测量在两个因子上载荷较为平均，这表明存在一个语言智力因子和一个非语言智力因子。

使用正交旋转将人为地强制两个因子不相关。如果想允许两个因子相关该怎么办呢？此时可以使用斜交转轴法，比如promax（见代码清单14-8）。

代码清单14-8　用斜交旋转提取因子

  1. > fa.promax <- fa(correlations, nfactors=2, rotate="promax", fm="pa")
  2. > fa.promax
  3. Factor Analysis using method =  pa
  4. Call: fa(r = correlations, nfactors = 2, rotate = "promax", fm = "pa")
  5. Standardized loadings based upon correlation matrix
  6.           PA1   PA2   h2   u2
  7. general  0.36  0.49 0.57 0.43
  8. picture -0.04  0.64 0.38 0.62
  9. blocks  -0.12  0.98 0.83 0.17
  10. maze    -0.01  0.45 0.20 0.80
  11. reading  1.01 -0.11 0.91 0.09
  12. vocab    0.84 -0.02 0.69 0.31
  14.                 PA1  PA2
  15. SS loadings    1.82 1.76
  16. Proportion Var 0.30 0.29
  17. Cumulative Var 0.30 0.60
  19.  With factor correlations of
  20.      PA1  PA2
  21. PA1 1.00 0.57
  22. PA2 0.57 1.00
  23. [……已删除额外输出……]

根据以上结果，你可以看出正交旋转和斜交旋转的不同之处。对于正交旋转，因子分析的重点在于因子结构矩阵（变量与因子的相关系数），而对于斜交旋转，因子分析会考虑三个矩阵：因子结构矩阵、因子模式矩阵和因子关联矩阵。

因子模式矩阵即标准化的回归系数矩阵。它列出了因子预测变量的权重。因子关联矩阵即因子相关系数矩阵。

在代码清单14-8中，PA1和PA2栏中的值组成了因子模式矩阵。它们是标准化的回归系数，而不是相关系数。注意，矩阵的列仍用来对因子进行命名（虽然此处存在一些争论）。你同样可以得到一个语言因子和一个非语言因子。

因子关联矩阵显示两个因子的相关系数为0.57，相关性很大。如果因子间的关联性很低，你可能需要重新使用正交旋转来简化问题。

因子结构矩阵（或称因子载荷阵）没有被列出来，但你可以使用公式F = P*Phi很轻松地得到它，其中F是因子载荷阵，P为因子模式矩阵，Phi为因子关联矩阵。下面的函数即可进行该乘法运算：

  1. fsm <- function(oblique) {
  2.   if (class(oblique)[2]=="fa" & is.null(oblique$Phi)) {
  3.        warning("Object doesn't look like oblique EFA")
  4.   } else {
  5.        P <- unclass(oblique$loading)
  6.        F <- P %*% oblique$Phi
  7.        colnames(F) <- c("PA1", "PA2")
  8.        return(F)
  9.   }
  10. }

对上面的例子使用该函数，可得：

  1. > fsm(fa.promax)
  2.          PA1  PA2
  3. general 0.64 0.69
  4. picture 0.33 0.61
  5. blocks  0.44 0.91
  6. maze    0.25 0.45
  7. reading 0.95 0.47
  8. vocab   0.83 0.46

现在你可以看到变量与因子间的相关系数。将它们与正交旋转所得因子载荷阵相比，你会发现该载荷阵列的噪音比较大，这是因为之前你允许潜在因子相关。虽然斜交方法更为复杂，但模型将更符合真实数据。

使用factor.plot()或fa.diagram()函数，你可以绘制正交或者斜交结果的图形。来看以下代码：

  1. factor.plot(fa.promax, labels=rownames(fa.promax$loadings))

它的生成图形见图14-5。

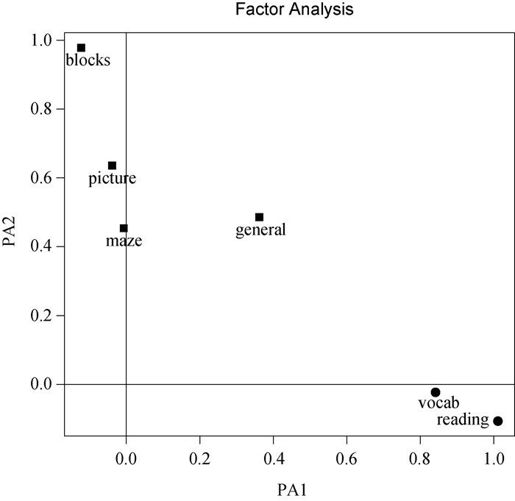
14.3　探索性因子分析 - 图3

图14-5　数据集ability.cov中心理学测验的两因子图形。词汇和阅读在第一个因子（PA1）上载荷较大，而积木图案、画图和迷宫在第二个因子（PA2）上载荷较大。普通智力测验在两个因子上较为平均

代码：

  1. fa.diagram(fa.promax, simple=FALSE)

生成的图形见图14-6。若使simple = TRUE，那么将仅显示每个因子下最大的载荷，以及因子间的相关系数。这类图形在有多个因子时十分实用。

当处理真实生活中的数据时，你不可能只对这么少的变量进行因子分析。此处只是为了操作方便，如果你想检测自己的能力，可尝试对Harman74.cor中的24个心理学测验进行因子分析。以下代码：

  1. library(psych)
  2. fa.24tests <- fa(Harman74.cor$cov, nfactors=4, rotate="promax")

应该是个不错的开头。

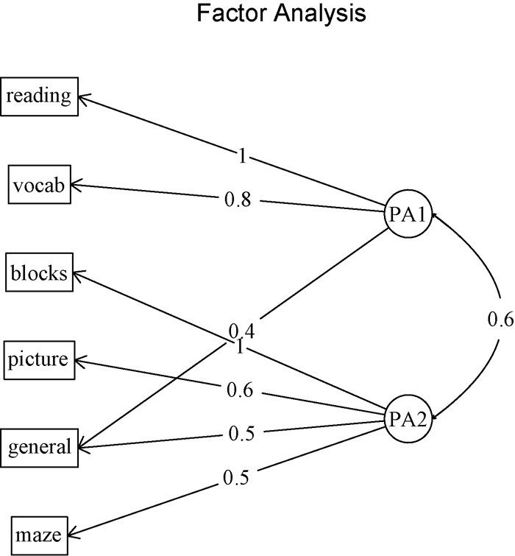
14.3　探索性因子分析 - 图4

图14-6　数据集ability.cov中心理学测验的两因子斜交旋转结果图

14.3.4　因子得分

相比PCA，EFA并不那么关注计算因子得分。在fa()函数中添加score = TRUE选项（原始数据可得时）便可很轻松地获得因子得分。另外还可以得到得分系数（标准化的回归权重），它在返回对象的weights元素中。

对于ability.cov数据集，通过二因子斜交旋转法便可获得用来计算因子得分的权重：

  1. > fa.promax$weights
  2.          [,1]  [,2]
  3. general 0.080 0.210
  4. picture 0.021 0.090
  5. blocks  0.044 0.695
  6. maze    0.027 0.035
  7. reading 0.739 0.044
  8. vocab   0.176 0.039

与可精确计算的主成分得分不同，因子得分只是估计得到的。它的估计方法有多种，fa()函数使用的是回归方法。若想更多地了解因子得分，可参阅DiStefano、Zhu和Mîndrilă的“Understanding and Using Factor Scores: Considerations for the Applied Researcher”（2009）。

在继续下文之前，让我们简单了解下其他用于探索性因子分析的实用R软件包。

14.3.5　其他与EFA相关的包

R包含了其他许多对因子分析非常有用的软件包。FactoMineR包不仅提供了PCA和EFA方法，还包含潜变量模型。它有许多此处我们并没考虑的参数选项，比如数值型变量和类别型变量的使用方法。FAiR包使用遗传算法来估计因子分析模型，它增强了模型参数估计能力，能够处理不等式的约束条件，GPArotation包则提供了许多因子旋转方法。最后，还有nFactors包，它提供了用来判断因子数目的许多复杂方法。