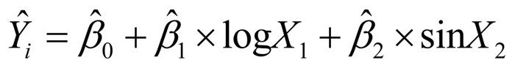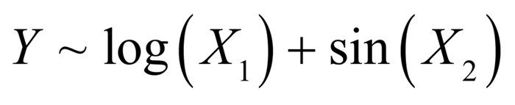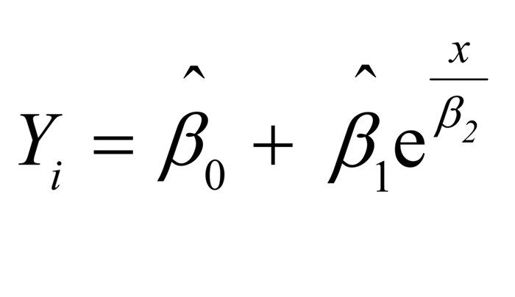8.2　OLS回归

在本章大部分内容中，我们都是利用OLS法通过一系列的预测变量来预测响应变量（也可以说是在预测变量上“回归”响应变量——其名也因此而来）。OLS回归拟合模型的形式：

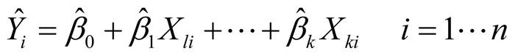
8.2　OLS回归 - 图1

其中，n 为观测的数目，k 为预测变量的数目。（虽然我极力避免讨论公式，但这里探讨公式是简化问题的需要。）等式中相应部分的解释如下。

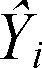8.2　OLS回归 - 图2 第i次观测对应的因变量的预测值（具体来讲，它是在已知预测变量值的条件下，对Y分布估计的均值）
Xji 第i次观测对应的第j个预测变量值
8.2　OLS回归 - 图3 截距项（当所有的预测变量都为0时，Y的预测值）
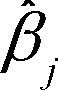8.2　OLS回归 - 图4 预测变量j的回归系数（斜率表示Xj改变一个单位所引起的Y的改变量）

我们的目标是通过减少响应变量的真实值与预测值的差值来获得模型参数（截距项和斜率）。具体而言，即使得残差平方和最小。

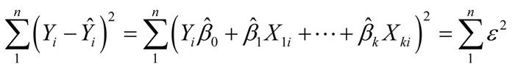
8.2　OLS回归 - 图5

为了能够恰当地解释OLS模型的系数，数据必须满足以下统计假设。

  • 正态性　对于固定的自变量值，因变量值成正态分布。

  • 独立性　Yi值之间相互独立。

  • 线性　因变量与自变量之间为线性相关。

  • 同方差性　因变量的方差不随自变量的水平不同而变化。也可称作不变方差，但是说同方差性感觉上更犀利。

如果违背了以上假设，你的统计显著性检验结果和所得的置信区间很可能就不精确。注意，OLS回归还假定自变量是固定的且测量无误差，但在实践中通常都放松了这个假设。

8.2.1　用lm()拟合回归模型

在R中，拟合线性模型最基本的函数就是lm()，格式为：

  1. myfit formula, data)

其中，formula指要拟合的模型形式，data是一个数据框，包含了用于拟合模型的数据。结果对象（本例中是myfit）存储在一个列表中，包含了所拟合模型的大量信息。表达式（formula）形式如下：

  1. Y ~ X1 + X2 + … + Xk

~左边为响应变量，右边为各个预测变量，预测变量之间用+符号分隔。表8-2中的符号可以不同方式修改这一表达式。 表8-2　R表达式中常用的符号

符　　号 用　　途
~ 分隔符号，左边为响应变量，右边为解释变量。例如，要通过x、z和w预测y，代码为y ~ x + z + w
+ 分隔预测变量
: 表示预测变量的交互项。例如，要通过x、z及x与z的交互项预测y，代码为y ~ x + z + x:z
* 表示所有可能交互项的简洁方式。代码y~ x * z * w可展开为y ~ x + z + w + x:z + x:w + z:w + x:z:w
^ 表示交互项达到某个次数。代码y ~ (x + z + w)^2可展开为y ~ x + z + w + x:z + x:w + z:w
. 表示包含除因变量外的所有变量。例如，若一个数据框包含变量x、y、z和w，代码y ~ .可展开为y ~ x + z + w
- 减号，表示从等式中移除某个变量。例如，y ~ (x + z + w)^2 – x:w可展开为y ~ x + z + w + x:z + z:w
-1 删除截距项。例如，表达式y ~ x - 1拟合y在x上的回归，并强制直线通过原点
I() 从算术的角度来解释括号中的元素。例如，y ~ x + (z + w)^2将展开为y ~ x + z + w + z:w。相反, 代码y ~ x + I((z + w)^2)将展开为y ~ x + h, h是一个由z和w的平方和创建的新变量
function 可以在表达式中用的数学函数。例如，log(y) ~ x + z + w表示通过x、z和w来预测log(y)

除了lm()，表8-3还列出了其他一些对做简单或多元回归分析有用的函数。拟合模型后，将这些函数应用于lm()返回的对象，可以得到更多额外的模型信息。 表8-3　对拟合线性模型非常有用的其他函数

函　　数 用　　途
summary() 展示拟合模型的详细结果
coefficients() 列出拟合模型的模型参数（截距项和斜率）
confint() 提供模型参数的置信区间（默认95%）
fitted() 列出拟合模型的预测值
residuals() 列出拟合模型的残差值
anova() 生成一个拟合模型的方差分析表，或者比较两个或更多拟合模型的方差分析表
vcov() 列出模型参数的协方差矩阵
AIC() 输出赤池信息统计量
plot() 生成评价拟合模型的诊断图
predict() 用拟合模型对新的数据集预测响应变量值

当回归模型包含一个因变量和一个自变量时，我们称为简单线性回归。当只有一个预测变量，但同时包含变量的幂（比如，X、X2、X3）时，我们称之为多项式回归。当有不止一个预测变量时，则称为多元线性回归。现在，我们首先从一个简单的线性回归例子开始，然后逐步展示多项式回归和多元线性回归，最后还会介绍一个包含交互项的多元线性回归的例子。

8.2.2　简单线性回归

让我们通过一个回归示例来熟悉表8-3中的函数。基础安装中的数据集women提供了15个年龄在30~39岁间女性的身高和体重信息，我们想通过身高来预测体重，获得一个等式可以帮助我们分辨出那些过重或过瘦的个体。代码清单8-1提供了分析过程，图8-1展示了结果图形。

代码清单8-1　简单线性回归

  1. > fit <- lm(weight ~ height, data=women)
  2. > summary(fit)
  3. Call:
  4. lm(formula=weight ~ height, data=women)
  6. Residuals:
  7.    Min     1Q Median     3Q    Max
  8. -1.733 -1.133 -0.383  0.742  3.117
  10. Coefficients:
  11.             Estimate Std. Error t value Pr(>|t|)
  12. (Intercept) -87.5167     5.9369   -14.7  1.7e-09 ***
  13. height        3.4500     0.0911    37.9  1.1e-14 ***
  14. ---
  15. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 '' 1
  17. Residual standard error: 1.53 on 13 degrees of freedom
  18. Multiple R-squared: 0.991,      Adjusted R-squared: 0.99
  19. F-statistic: 1.43e+03 on 1 and 13 DF,  p-value: 1.09e-14
  21. > women$weight
  23.  [1] 115 117 120 123 126 129 132 135 139 142 146 150 154 159 164
  25. > fitted(fit)
  27.      1      2      3      4      5      6      7      8      9
  28. 112.58 116.03 119.48 122.93 126.38 129.83 133.28 136.73 140.18
  29.     10     11     12     13     14     15
  30. 143.63 147.08 150.53 153.98 157.43 160.88
  32. > residuals(fit)
  34.     1     2     3     4     5     6     7     8     9    10    11
  35.  2.42  0.97  0.52  0.07 -0.38 -0.83 -1.28 -1.73 -1.18 -1.63 -1.08
  36.   12     13    14    15
  37. -0.53  0.02  1.57  3.12
  39. > plot(women$height,women$weight,
  40.     xlab="Height (in inches)",
  41.     ylab="Weight (in pounds)")
  42. > abline(fit)

通过输出结果，可以得到预测等式：

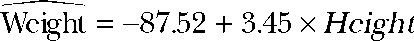
8.2　OLS回归 - 图6

因为身高不可能为0，你没必要给截距项一个物理解释，它仅仅是一个常量调整项。在Pr(>|t|)栏，可以看到回归系数（3.45）显著不为0（p<0.001），表明身高每增高1英寸，体重将预期增加3.45磅1。R平方项（0.991）表明模型可以解释体重99.1%的方差，它也是实际和预测值之间的相关系数（R2 = r2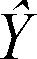8.2　OLS回归 - 图7Y）。残差标准误（1.53 lbs）则可认为是模型用身高预测体重的平均误差。F统计量检验所有的预测变量预测响应变量是否都在某个几率水平之上。由于简单回归只有一个预测变量，此处F检验等同于身高回归系数的t检验。

1 1英寸≈2.54厘米，1磅≈0.45千克。——编者注

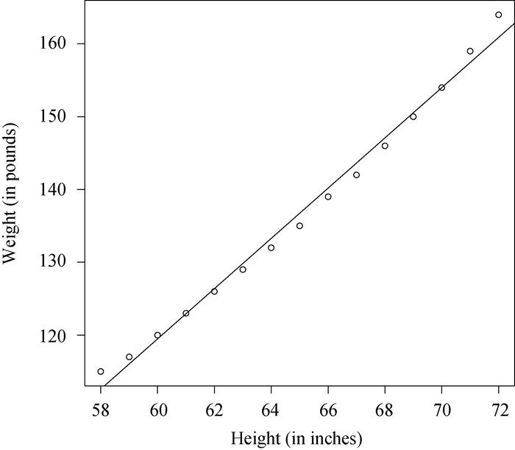
8.2　OLS回归 - 图8

图8-1　用身高预测体重的散点图以及回归线

为了展示的需要，我们已经输出了真实值、预测值和残差值。显然，最大的残差值在身高矮和身高高的地方出现，这也可以从图8-1看出来。

图形表明你可以用含一个弯曲的曲线来提高预测的精度。比如，模型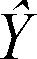8.2　OLS回归 - 图9 = β0 + β1X + β1X2就能更好地拟合数据。多项式回归允许你用一个解释变量预测一个响应变量，它们关系的形式即n次多项式。

8.2.3　多项式回归

图8-1表明，你可以通过添加一个二次项（即X2）来提高回归的预测精度。

如下代码可以拟合含二次项的等式：

  1. fit2 <- lm(weight ~ height + I(height^2), data=women)

I(height^2)表示向预测等式添加一个身高的平方项。I函数将括号的内容看做R的一个常规表达式。因为^（参见表8-2）符号在表达式中有特殊的含义，会调用你并不需要的东西，所以此处必须要用这个函数。

代码清单8-2展示了拟合含二次项等式的结果。

代码清单8-2　多项式回归

  1. > fit2 <- lm(weight ~ height + I(height^2), data=women)
  2. > summary(fit2)
  4. Call:
  5. lm(formula=weight ~ height + I(height^2), data=women)
  7. Residuals:
  8.     Min      1Q  Median      3Q     Max
  9. -0.5094 -0.2961 -0.0094  0.2862  0.5971
  11. Coefficients:
  12.              Estimate Std. Error t value Pr(>|t|)
  13. (Intercept) 261.87818   25.19677   10.39  2.4e-07 ***
  14. height       -7.34832    0.77769   -9.45  6.6e-07 ***
  15. I(height^2)   0.08306    0.00598   13.89  9.3e-09 ***
  16. ---
  17. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  19. Residual standard error: 0.384 on 12 degrees of freedom
  20. Multiple R-squared: 0.999,      Adjusted R-squared: 0.999
  21. F-statistic: 1.14e+04 on 2 and 12 DF,  p-value: <2e-16
  23. > plot(women$height,women$weight,
  24.     xlab="Height (in inches)",
  25.     ylab="Weight (in lbs)")
  26. > lines(women$height,fitted(fit2))

新的预测等式为：

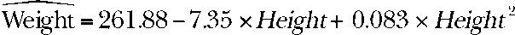
8.2　OLS回归 - 图10

在p<0.001水平下，回归系数都非常显著。模型的方差解释率已经增加到了99.9%。二次项的显著性（t = 13.89，p<0.001）表明包含二次项提高了模型的拟合度。从图8-2也可以看出曲线确实拟合得较好。

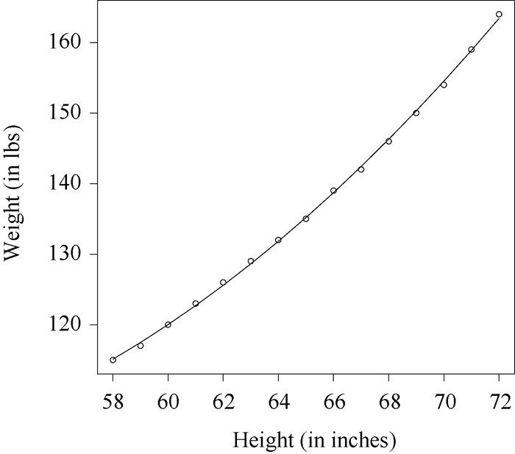
8.2　OLS回归 - 图11

图8-2　用身高预测体重的二次回归

线性模型与非线性模型

多项式等式仍可认为是线性回归模型，因为等式仍是预测变量的加权和形式（本例中是身高和身高的平方）。即使这样的模型：

8.2　OLS回归 - 图12

仍可认为是线性模型（参数项是线性的），能用这样的表达式进行拟合：

8.2　OLS回归 - 图13

相反，下面的例子才能算是真正的非线性模型：

8.2　OLS回归 - 图14

这种非线性模型可用nls()函数进行拟合。

一般来说，n次多项式生成一个n-1个弯曲的曲线。拟合三次多项式，可用：

  1. fit3 <- lm(weight ~ height + I(height^2) +I(height^3), data=women)

虽然更高次的多项式也可用，但我发现使用比三次更高的项几乎没有必要。

在继续下文之前，我还得提及car包中的scatterplot()函数，它可以很容易、方便地绘制二元关系图。以下代码能生成图8-3所示的图形。

  1. library(car)
  2. scatterplot(weight ~ height,
  3.    data=women,
  4.   spread=FALSE, lty.smooth=2,
  5.    pch=19,
  6.   main="Women Age 30-39",
  7.   xlab="Height (inches)",
  8.   ylab="Weight (lbs.)")

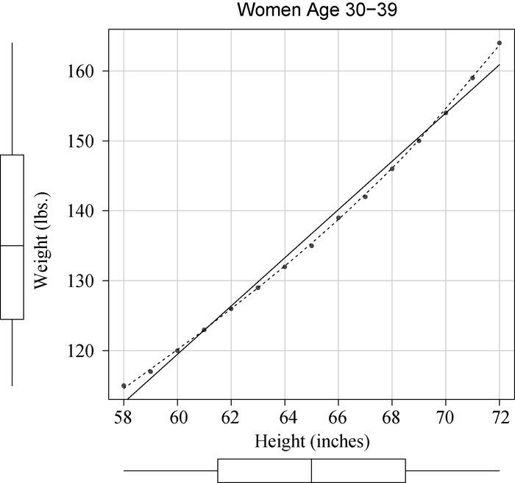
8.2　OLS回归 - 图15

图8-3　身高与体重的散点图。直线为线性拟合，虚线为曲线平滑拟合，边界为箱线图

这个功能加强的图形，既提供了身高与体重的散点图、线性拟合曲线和平滑拟合（loess）曲线，还在相应边界展示了每个变量的箱线图。spread=FALSE选项删除了残差正负均方根在平滑曲线上的展开和非对称信息。lty.smooth=2选项设置loess拟合曲线为虚线。pch=19选项设置点为实心圆（默认为空心圆）。粗略地看一下图8-3可知，两个变量基本对称，曲线拟合得比直线更好。

8.2.4　多元线性回归

当预测变量不止一个时，简单线性回归就变成了多元线性回归，分析也稍微复杂些。从技术上来说，多项式回归可以算是多元线性回归的特例：二次回归有两个预测变量（X和X2），三次回归有三个预测变量（X、X2和X3）。现在让我们看一个更一般的例子。

以基础包中的state.x77数据集为例，我们想探究一个州的犯罪率和其他因素的关系，包括人口、文盲率、平均收入和结霜天数（温度在冰点以下的平均天数）。

因为lm()函数需要一个数据框（state.x77数据集是矩阵），为了以后处理方便，你需要做如下转化：

  1. states <- as.data.frame(state.x77[,c("Murder", "Population",
  2.          "Illiteracy", "Income", "Frost")])

这行代码创建了一个名为states的数据框，包含了我们感兴趣的变量。本章的余下部分，我们都将使用这个新的数据框。

多元回归分析中，第一步最好检查一下变量间的相关性。cor()函数提供了二变量之间的相关系数，car包中scatterplotMatrix()函数则会生成散点图矩阵（参见代码清单8-3和图8-4）。

代码清单8-3　检测二变量关系

  1. > cor(states)
  2.            Murder Population Illiteracy Income Frost
  3. Murder       1.00       0.34       0.70  -0.23 -0.54
  4. Population   0.34       1.00       0.11   0.21 -0.33
  5. Illiteracy   0.70       0.11       1.00  -0.44 -0.67
  6. Income      -0.23       0.21      -0.44   1.00  0.23
  7. Frost       -0.54      -0.33      -0.67   0.23  1.00
  9. > library(car)
  10. > scatterplotMatrix(states, spread=FALSE, lty.smooth=2,
  11.     main="Scatter Plot Matrix")

scatterplotMatrix()函数默认在非对角线区域绘制变量间的散点图，并添加平滑（loess）和线性拟合曲线。对角线区域绘制每个变量的密度图和轴须图。

从图中可以看到，谋杀率是双峰的曲线，每个预测变量都一定程度上出现了偏斜。谋杀率随着人口和文盲率的增加而增加，随着收入水平和结霜天数增加而下降。同时，越冷的州府文盲率越低，收入水平越高。

现在使用lm()函数拟合多元线性回归模型（参见代码清单8-4）。

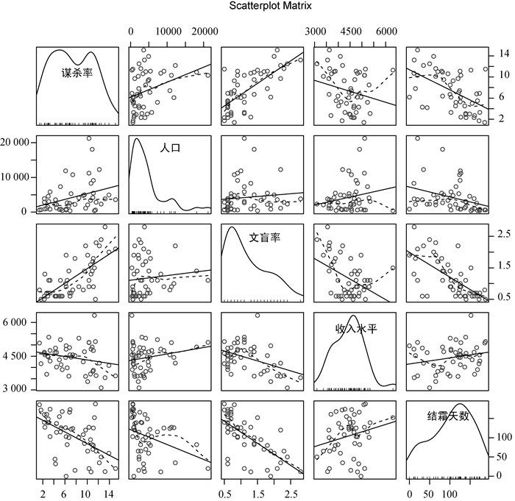
8.2　OLS回归 - 图16

图8-4　州府数据中因变量与自变量的散点图矩阵。［包含线性和平滑拟合曲线，以及相应的边际分布（核密度图和轴须图）］

代码清单8-4　多元线性回归

  1. > fit <- lm(Murder ~ Population + Illiteracy + Income + Frost,
  2.             data=states)
  3. > summary(fit)
  5. Call:
  6. lm(formula=Murder ~ Population + Illiteracy + Income + Frost,
  7.     data=states)
  9. Residuals:
  10.     Min      1Q  Median      3Q     Max
  11. -4.7960 -1.6495 -0.0811  1.4815  7.6210
  13. Coefficients:
  14.             Estimate Std. Error t value Pr(>|t|)
  15. (Intercept) 1.23e+00   3.87e+00    0.32    0.751
  16. Population  2.24e-04   9.05e-05    2.47    0.017 *
  17. Illiteracy  4.14e+00   8.74e-01    4.74  2.2e-05 ***
  18. Income      6.44e-05   6.84e-04    0.09    0.925
  19. Frost       5.81e-04   1.01e-02    0.06    0.954
  20. ---
  21. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.v 0.1 'v' 1
  23. Residual standard error: 2.5 on 45 degrees of freedom
  24. Multiple R-squared: 0.567,      Adjusted R-squared: 0.528
  25. F-statistic: 14.7 on 4 and 45 DF,  p-value: 9.13e-08

当预测变量不止一个时，回归系数的含义为，一个预测变量增加一个单位，其他预测变量保持不变时，因变量将要增加的数量。例如本例中，文盲率的回归系数为4.14，表示控制人口、收入和温度不变时，文盲率上升1%，谋杀率将会上升4.14%，它的系数在p<0.001的水平下显著不为0。相反，Frost的系数没有显著不为0（p=0.954），表明当控制其他变量不变时，Frost与Murder不呈线性相关。总体来看，所有的预测变量解释了各州谋杀率57%的方差。

以上分析中，我们没有考虑预测变量的交互项，在接下来的章节中，我们将考虑一个包含此因素的例子。

8.2.5　有交互项的多元线性回归

许多很有趣的研究都会涉及交互项的预测变量。以mtcars数据框中的汽车数据为例，若你对汽车重量和马力感兴趣，可以把它们作为预测变量，并包含交互项来拟合回归模型，参见代码清单8-5。

代码清单8-5　有显著交互项的多元线性回归

  1. > fit <- lm(mpg ~ hp + wt + hp:wt, data=mtcars)
  2. > summary(fit)
  4. Call:
  5. lm(formula=mpg ~ hp + wt + hp:wt, data=mtcars)
  7. Residuals:
  8.    Min     1Q Median     3Q    Max
  9. -3.063 -1.649 -0.736  1.421  4.551
  11. Coefficients:
  12.             Estimate Std. Error t value Pr(>|t|)
  13. (Intercept) 49.80842    3.60516   13.82  5.0e-14 ***
  14. hp          -0.12010    0.02470   -4.86  4.0e-05 ***
  15. wt          -8.21662    1.26971   -6.47  5.2e-07 ***
  16. hp:wt        0.02785    0.00742    3.75  0.00081 ***
  17. ---
  18. Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
  20. Residual standard error: 2.1 on 28 degrees of freedom
  21. Multiple R-squared: 0.885,      Adjusted R-squared: 0.872
  22. F-statistic: 71.7 on 3 and 28 DF,  p-value: 2.98e-13

你可以看到Pr(>|t|)栏中，马力与车重的交互项是显著的，这意味着什么呢？若两个预测变量的交互项显著，说明响应变量与其中一个预测变量的关系依赖于另外一个预测变量的水平。因此此例说明，每加仑汽油行驶英里数与汽车马力的关系依车重不同而不同。

预测mpg的模型为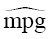8.2　OLS回归 - 图17 = 49.81 - 0.12×hp - 8.22×wt + 0.03×hp×wt。为更好地理解交互项，你可以赋给wt不同的值，并简化等式。例如，可以试试wt的均值（3.2），少于均值一个标准差和多于均值一个标准差的值（分别是2.2和4.2）。若wt = 2.2，则等式可以化简为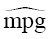8.2　OLS回归 - 图18 = 49.81 - 0.12×hp - 8.22×(2.2) + 0.03×hp×(2.2) = 31.41 - 0.06×hp；若wt = 3.2，则变成了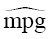8.2　OLS回归 - 图19 = 23.37 - 0.03×hp；若wt = 4.2，则等式为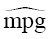8.2　OLS回归 - 图20 = 15.33 - 0.003×hp。你将发现，随着车重增加（2.2、3.2、4.2），hp每增加一个单位引起的mpg预期改变却在减少（0.06、0.03、0.003）。

通过effects包中的effect()函数，你可以用图形展示交互项的结果。格式为：

  1. plot(effect(term, mod, xlevels),
  2.   multiline=TRUE)

term即模型要画的项，mod为通过lm()拟合的模型，xlevels是一个列表，指定变量要设定的常量值，multiline=TRUE选项表示添加相应直线。对于上例，即：

  1. library(effects)
  2. plot(effect("hp:wt", fit,
  3.   list(wt=c(2.2,3.2,4.2))),
  4.   multiline=TRUE)

结果展示在图8-5中。

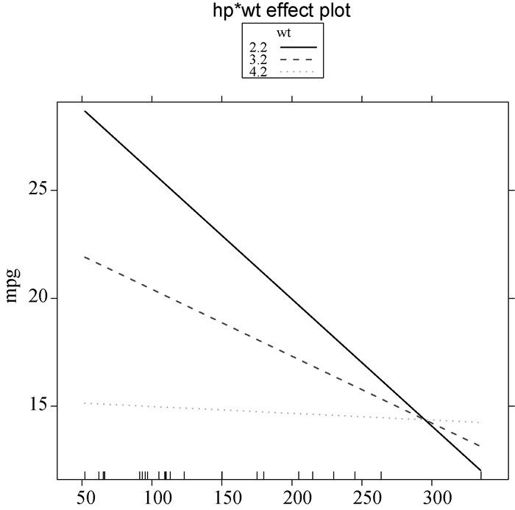
8.2　OLS回归 - 图21

图8-5　hp*wt的交互项图形。图形展示了wt三种值时mpg和hp的关系

从图中可以很清晰地看出，随着车重的增加，马力与每加仑汽油行驶英里数的关系减弱了。当wt = 4.2时，直线几乎是水平的，表明随着hp的增加，mpg不会发生改变。

然而，拟合模型只不过是分析的第一步，一旦拟合了回归模型，在信心十足地进行推断之前，必须对方法中暗含的统计假设进行检验。这正是下节的主题。