15.7　多重插补

多重插补（MI）是一种基于重复模拟的处理缺失值的方法。在面对复杂的缺失值问题时，MI是最常选用的方法，它将从一个包含缺失值的数据集中生成一组完整的数据集（通常是3到10个）。每个模拟数据集中，缺失数据将用蒙特卡洛方法来填补。此时，标准的统计方法便可应用到每个模拟的数据集上，通过组合输出结果给出估计的结果，以及引入缺失值时的置信区间。R中可利用Amelia、mice和mi包来执行这些操作。本节中，我们将重点学习mice包（利用链式方程的多元插补）提供的方法。

图15-5可以帮助理解mice包的操作过程。

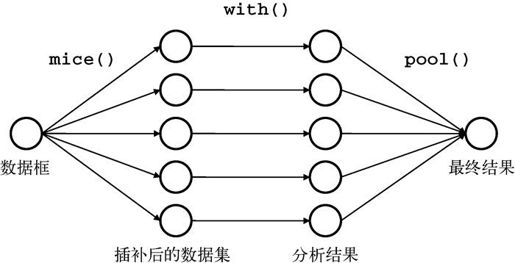
15.7　多重插补 - 图1

图15-5　通过mice包应用多重插补的步骤

函数mice()首先从一个包含缺失数据的数据框开始，然后返回一个包含多个（默认为5个）完整数据集的对象。每个完整数据集都是通过对原始数据框中的缺失数据进行插补而生成的。由于插补有随机的成分，因此每个完整数据集都略有不同。然后，with()函数可依次对每个完整数据集应用统计模型（如线性模型或广义线性模型），最后，pool()函数将这些单独的分析结果整合为一组结果。最终模型的标准误和p值都将准确地反映出由于缺失值和多重插补而产生的不确定性。

mice()函数如何插补缺失值？

缺失值的插补通过Gibbs抽样完成。每个包含缺失值的变量都默认可通过数据集中的其他变量预测得来，于是这些预测方程便可用来预测缺失数据的有效值。该过程不断迭代直到所有的缺失值都收敛为止。对于每个变量，用户可以选择预测模型的形式（称为基本插补法）和待选入的变量。

默认地，预测的均值用来替换连续型变量中的缺失数据，而Logistic或多元Logistic回归则分别用来替换二值目标变量（两水平因子）或多值变量（多于两水平的因子）。其他基本插补法包括贝叶斯线性回归、判别分析、两水平正态插补和从观测值中随机抽样。用户也可以选择自己独有的方法。

基于mice包的分析通常符合以下分析过程：

  1. library(mice)
  2. imp <- mice(mydata, m)
  3. fit <- with(imp, analysis)
  4. pooled <- pool(fit)
  5. summary(pooled)

  • mydata是一个包含缺失值的矩阵或数据框。

  • imp是一个包含m个插补数据集的列表对象，同时还含有完成插补过程的信息。默认地，m为5。

  • analysis是一个表达式对象，用来设定应用于m个插补数据集的统计分析方法。方法包括做线性回归模型的lm()函数、做广义线性模型的glm()函数、做广义可加模型的gam()，以及做负二项模型的nbrm()函数。表达式在函数的括号中，~的左边是响应变量，右边是预测变量（用+符号分隔开）。

  • fit是一个包含m个单独统计分析结果的列表对象。

  • pooled是一个包含这m个统计分析平均结果的列表对象。

现将多重插补法应用到sleep数据集上。重复15.6节的分析过程，不过此处我们将利用所有的62个动物。设定随机种子为1234，这样你的结果将和我的分析结果一样：

  1. > library(mice)
  2. > data(sleep, package="VIM")
  3. > imp <- mice(sleep, seed=1234)
  5.  […output deleted to save space…]
  7. > fit <- with(imp, lm(Dream ~ Span + Gest))
  8. > pooled <- pool(fit)
  9. > summary(pooled)
  10.                  est      se      t   df Pr(>|t|)    lo 95
  11. (Intercept)  2.58858 0.27552  9.395 52.1 8.34e-13  2.03576
  12. Span        -0.00276 0.01295 -0.213 52.9 8.32e-01 -0.02874
  13. Gest        -0.00421 0.00157 -2.671 55.6 9.91e-03 -0.00736
  14.                hi 95 nmis    fmi
  15. (Intercept)  3.14141   NA 0.0870
  16. Span         0.02322    4 0.0806
  17. Gest        -0.00105    4 0.0537

此处，你可以看到Span的回归系数不显著（p ≈ 0.08 ），Gest的系数在 p < 0.01的水平下很显著。若将这些结果与利用完整数据分析法（15.6节）所得的结果对比，你会发现背离的结论相同。当控制寿命不变时，妊娠期与做梦时长有一个（统计）显著的、负相关的关系。完整数据分析法基于42个有完整数据的动物，而此处的分析法基于整个数据集中全部62个动物的数据。另外，fmi栏也展示了缺失信息（即由于引入了缺失数据而引起的变异所占整体不确定性的比例）。

你可以通过检查分析过程所创建的对象来获取更多的插补信息。例如，来看imp对象的汇总信息：

  1. > imp
  3. Multiply imputed data set
  4. Call:
  5. mice(data = sleep, seed = 1234)
  6. Number of multiple imputations:  5
  7. Missing cells per column:
  8.  BodyWgt BrainWgt     NonD    Dream    Sleep     Span     Gest     Pred
  9.        0        0       14       12        4        4        4        0
  10.      Exp   Danger
  11.        0        0
  12. Imputation methods:
  13.  BodyWgt BrainWgt     NonD    Dream    Sleep     Span     Gest     Pred
  14.       ""       ""    "pmm"    "pmm"    "pmm"    "pmm"    "pmm"       ""
  15.      Exp   Danger
  16.       ""       ""
  17. VisitSequence:
  18.  NonD Dream Sleep  Span  Gest
  19.     3     4     5     6     7
  20. PredictorMatrix:
  21.          BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
  22. BodyWgt        0        0    0     0     0    0    0    0   0      0
  23. BrainWgt       0        0    0     0     0    0    0    0   0      0
  24. NonD           1        1    0     1     1    1    1    1   1      1
  25. Dream          1        1    1     0     1    1    1    1   1      1
  26. Sleep          1        1    1     1     0    1    1    1   1      1
  27. Span           1        1    1     1     1    0    1    1   1      1
  28. Gest           1        1    1     1     1    1    0    1   1      1
  29. Pred           0        0    0     0     0    0    0    0   0      0
  30. Exp            0        0    0     0     0    0    0    0   0      0
  31. Danger         0        0    0     0     0    0    0    0   0      0
  32. Random generator seed value:  1234

从输出结果可以看到，五个数据集同时被创建，预测均值（pmm）匹配法被用来处理每个含缺失数据的变量。BodyWgt、BrainWgt、Pred、Exp和Danger没有进行插补（" "），因为它们并没有缺失数据。VisitSequence从左至右展示了插补的变量，从NonD开始，以Gest结束。最后，预测变量矩阵（PredictorMatrix）展示了进行插补过程的含有缺失数据的变量，它们利用了数据集中其他变量的信息。（在矩阵中，行代表插补变量，列代表为插补提供信息的变量，1和0分别表示使用和未使用。）

通过提取imp对象的子成分，可以观测到实际的插补值。如：

  1. > imp$imp$Dream
  2.      1   2   3   4   5
  3. 1  0.5 0.5 0.5 0.5 0.0
  4. 3  2.3 2.4 1.9 1.5 2.4
  5. 4  1.2 1.3 5.6 2.3 1.3
  6. 14 0.6 1.0 0.0 0.3 0.5
  7. 24 1.2 1.0 5.6 1.0 6.6
  8. 26 1.9 6.6 0.9 2.2 2.0
  9. 30 1.0 1.2 2.6 2.3 1.4
  10. 31 5.6 0.5 1.2 0.5 1.4
  11. 47 0.7 0.6 1.4 1.8 3.6
  12. 53 0.7 0.5 0.7 0.5 0.5
  13. 55 0.5 2.4 0.7 2.6 2.6
  14. 62 1.9 1.4 3.6 5.6 6.6

展示了在Dream变量上有缺失值的12个动物的5次插补值。检查该矩阵可以帮助你判断插补值是否合理。若睡眠时长出现了负值，插补将会停止（否则结果将会很糟糕）。

利用complete()函数可以观察m个插补数据集中的任意一个。格式为：

  1. complete(imp, action=#)

其中#指定m个完整数据集中的一个来展示，比如：

  1. > dataset3 <- complete(imp, action=3)
  2. > dataset3
  3.   BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
  4. 1 6654.00   5712.0  2.1   0.5   3.3 38.6  645    3   5      3
  5. 2    1.00      6.6  6.3   2.0   8.3  4.5   42    3   1      3
  6. 3    3.38     44.5 10.6   1.9  12.5 14.0   60    1   1      1
  7. 4    0.92      5.7 11.0   5.6  16.5  4.7   25    5   2      3
  8. 5 2547.00   4603.0  2.1   1.8   3.9 69.0  624    3   5      4
  9. 6   10.55    179.5  9.1   0.7   9.8 27.0  180    4   4      4
  10. […output deleted to save space…]

展示了多重插补过程中创建的第三个完整数据集。

由于篇幅限制，此处我们只是简略介绍了mice包提供的多重插补法（MI）。mi和Amelia包也提供了一些有用的方法。如果你对缺失值的多重插补法感兴趣，可以参考以下学习资源：

上述每个资源都能加深你对这些虽然未充分利用但却十分重要的方法的理解。