13.2　Logistic回归

当通过一系列连续型和/或类别型预测变量来预测二值型结果变量时，Logistic回归是一个非常有用的工具。以AER包中的数据框Affairs为例，我们将通过探究婚外情的数据来阐述Logistic回归的过程。首次使用该数据前，请确保已下载和安装此软件包（使用install.packages("AER")）。

婚外情数据即著名的“Fair's Affairs”，取自于1969年《今日心理》（Psychology Today）所做的一个非常有代表性的调查，而Greene（2003）和Fair（1978）都对它进行过分析。该数据从601个参与者身上收集了9个变量，包括一年来婚外私通的频率以及参与者性别、年龄、婚龄、是否有小孩、宗教信仰程度（5分制，1分表示反对，5分表示非常信仰）、学历、职业（逆向编号的戈登7种分类），还有对婚姻的自我评分（5分制，1表示非常不幸福，5表示非常幸福）。

我们先看一些描述性的统计信息：

  1. > data(Affairs, package="AER")
  2. > summary(Affairs)
  3.     affairs          gender         age         yearsmarried    children
  4.  Min.   : 0.000   female:315   Min.   :17.50   Min.   : 0.125   no :171
  5.  1st Qu.: 0.000   male  :286   1st Qu.:27.00   1st Qu.: 4.000   yes:430
  6.  Median : 0.000                Median :32.00   Median : 7.000
  7.  Mean   : 1.456                Mean   :32.49   Mean   : 8.178
  8.  3rd Qu.: 0.000                3rd Qu.:37.00   3rd Qu.:15.000
  9.  Max.   :12.000                Max.   :57.00   Max.   :15.000
  10.  religiousness     education       occupation        rating
  11.  Min.   :1.000   Min.   : 9.00   Min.   :1.000   Min.   :1.000
  12.  1st Qu.:2.000   1st Qu.:14.00   1st Qu.:3.000   1st Qu.:3.000
  13.  Median :3.000   Median :16.00   Median :5.000   Median :4.000
  14.  Mean   :3.116   Mean   :16.17   Mean   :4.195   Mean   :3.932
  15.  3rd Qu.:4.000   3rd Qu.:18.00   3rd Qu.:6.000   3rd Qu.:5.000
  16.  Max.   :5.000   Max.   :20.00   Max.   :7.000   Max.   :5.000
  18. > table(Affairs$affairs)
  19.   0   1   2   3   7  12
  20. 451  34  17  19  42  38

从这些统计信息可以看到，52%的调查对象是女性，72%的人有孩子，样本年龄的中位数为32岁。对于响应变量，72%的调查对象表示过去一年中没有婚外情（451/601），而婚外偷腥的最多次数为12（占了6%）。

虽然这些婚姻的轻率举动次数被记录下来，但此处我们感兴趣的是二值型结果（有过一次婚外情/没有过婚外情）。按照如下代码，你可将affairs转化为二值型因子ynaffair。

  1. > Affairs$ynaffair[Affairs$affairs > 0]  <- 1
  2. > Affairs$ynaffair[Affairs$affairs == 0] <- 0
  3. > Affairs$ynaffair <- factor(Affairs$ynaffair,
  4.                              levels=c(0,1),
  5.                              labels=c("No","Yes"))
  6. > table(Affairs$ynaffair)
  7. No Yes
  8. 451 150

该二值型因子现可作为Logistic回归的结果变量：

  1. > fit.full <- glm(ynaffair ~ gender + age + yearsmarried + children +
  2.                   religiousness + education + occupation +rating,
  3.                   data=Affairs,family=binomial())
  5. > summary(fit.full)
  7. Call:
  8. glm(formula = ynaffair ~ gender + age + yearsmarried + children +
  9.     religiousness + education + occupation + rating, family = binomial(),
  10.     data = Affairs)
  12. Deviance Residuals:
  13.    Min      1Q  Median      3Q     Max
  14. -1.571  -0.750  -0.569  -0.254   2.519
  16. Coefficients:
  17.               Estimate Std. Error z value Pr(>|z|)
  18. (Intercept)     1.3773     0.8878    1.55  0.12081
  19. gendermale      0.2803     0.2391    1.17  0.24108
  20. age            -0.0443     0.0182   -2.43  0.01530 *
  21. yearsmarried    0.0948     0.0322    2.94  0.00326 **
  22. childrenyes     0.3977     0.2915    1.36  0.17251
  23. religiousness  -0.3247     0.0898   -3.62  0.00030 ***
  24. education       0.0211     0.0505    0.42  0.67685
  25. occupation      0.0309     0.0718    0.43  0.66663
  26. rating         -0.4685     0.0909   -5.15  2.6e-07 ***
  27. ---
  28. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  30. (Dispersion parameter for binomial family taken to be 1)
  32.     Null deviance: 675.38  on 600  degrees of freedom
  33. Residual deviance: 609.51  on 592  degrees of freedom
  34. AIC: 627.5
  36. Number of Fisher Scoring iterations: 4

从回归系数的p值（最后一栏）可以看到，性别、是否有孩子、学历和职业对方程的贡献都不显著（你无法拒绝参数为0的假设）。去除这些变量重新拟合模型，检验新模型是否拟合得好：

  1. > fit.reduced <- glm(ynaffair ~ age + yearsmarried + religiousness +
  2.                      rating, data=Affairs, family=binomial())
  3. > summary(fit.reduced)
  5. Call:
  6. glm(formula = ynaffair ~ age + yearsmarried + religiousness + rating,
  7.     family = binomial(), data = Affairs)
  9. Deviance Residuals:
  10.    Min      1Q  Median      3Q     Max
  11. -1.628  -0.755  -0.570  -0.262   2.400
  13. Coefficients:
  14.               Estimate Std. Error z value Pr(>|z|)
  15. (Intercept)     1.9308     0.6103    3.16  0.00156 **
  16. age            -0.0353     0.0174   -2.03  0.04213 *
  17. yearsmarried    0.1006     0.0292    3.44  0.00057 ***
  18. religiousness  -0.3290     0.0895   -3.68  0.00023 ***
  19. rating         -0.4614     0.0888   -5.19  2.1e-07 ***
  20. ---
  21. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  23. (Dispersion parameter for binomial family taken to be 1)
  25.     Null deviance: 675.38 on 600 degrees of freedom
  26. Residual deviance: 615.36 on 596 degrees of freedom
  27. AIC: 625.4
  29. Number of Fisher Scoring iterations: 4

新模型的每个回归系数都非常显著（p<0.05）。由于两模型嵌套（fit.reduced是fit.full的一个子集），你可以使用anova()函数对它们进行比较，对于广义线性回归，可用卡方检验。

  1. > anova(fit.reduced, fit.full, test="Chisq")
  2. Analysis of Deviance Table
  4. Model 1: ynaffair ~ age + yearsmarried + religiousness + rating
  5. Model 2: ynaffair ~ gender + age + yearsmarried + children +
  6.     religiousness + education + occupation + rating
  7.   Resid. Df Resid. Dev Df Deviance P(>|Chi|)
  8. 1       596        615
  9. 2       592        610  4     5.85      0.21

结果的卡方值不显著（p=0.21），表明四个预测变量的新模型与九个完整预测变量的模型拟合程度一样好。这使得你更加坚信添加性别、孩子、学历和职业变量不会显著提高方程的预测精度，因此可以依据更简单的模型进行解释。

13.2.1　解释模型参数

先看看回归系数：

  1. > coef(fit.reduced)
  2.   (Intercept)           age  yearsmarried religiousness       rating
  3.         1.931        -0.035  0.101               -0.329       -0.461

在Logistic回归中，响应变量是Y=1的对数优势比（log）。回归系数含义是当其他预测变量不变时，一单位预测变量的变化可引起的响应变量对数优势比的变化。

由于对数优势比解释性差，你可对结果进行指数化：

  1. > exp(coef(fit.reduced))
  2.   (Intercept)           age  yearsmarried religiousness       rating
  3.         6.895         0.965         1.106         0.720        0.630

可以看到婚龄增加一年，婚外情的优势比将乘以1.106（保持年龄、宗教信仰和婚姻评定不变）；相反，年龄增加一岁，婚外情的的优势比则乘以0.965。因此，随着婚龄的增加和年龄、宗教信仰与婚姻评分的降低，婚外情优势比将上升。因为预测变量不能等于0，截距项在此处没有什么特定含义。

如果有需要，你还可使用confint()函数获取系数的置信区间。例如，exp(confint (fit.reduced))可在优势比尺度上得到系数95%的置信区间。

最后，预测变量一单位的变化可能并不是我们最想关注的。对于二值型Logistic回归，某预测变量n单位的变化引起的较高值上优势比的变化为exp(βj)^n，它反映的信息可能更为重要。比如，保持其他预测变量不变，婚龄增加一年，婚外情的优势比将乘以1.106，而如果婚龄增加10年，优势比将乘以1.106^10，即2.7。

13.2.2　评价预测变量对结果概率的影响

对于我们大多数人来说，以概率的方式思考比使用优势比更直观。使用predict()函数，你可观察某个预测变量在各个水平时对结果概率的影响。首先创建一个包含你感兴趣预测变量值的虚拟数据集，然后对该数据集使用predict()函数，以预测这些值的结果概率。

现在我们使用该方法评价婚姻评分对婚外情概率的影响。首先，创建一个虚拟数据集，设定年龄、婚龄和宗教信仰为它们的均值，婚姻评分的范围为1～5。

  1. > testdata <- data.frame(rating=c(1, 2, 3, 4, 5), age=mean(Affairs$age),
  2.                          yearsmarried=mean(Affairs$yearsmarried),
  3.                          religiousness=mean(Affairs$religiousness))
  4. > testdata
  5.   rating  age yearsmarried religiousness
  6. 1      1 32.5         8.18          3.12
  7. 2      2 32.5         8.18          3.12
  8. 3      3 32.5         8.18          3.12
  9. 4      4 32.5         8.18          3.12
  10. 5      5 32.5         8.18          3.12

接下来，使用测试数据集预测相应的概率：

  1. > testdata$prob <- predict(fit.reduced, newdata=testdata, type="response")
  2.   testdata
  3.   rating  age yearsmarried religiousness  prob
  4. 1      1 32.5         8.18          3.12 0.530
  5. 2      2 32.5         8.18          3.12 0.416
  6. 3      3 32.5         8.18          3.12 0.310
  7. 4      4 32.5         8.18          3.12 0.220
  8. 5      5 32.5         8.18          3.12 0.151

从这些结果可以看到，当婚姻评分从1（很不幸福）变为5（非常幸福）时，婚外情概率从0.53降低到了0.15（假定年龄、婚龄和宗教信仰不变）。下面我们再看看年龄的影响：

  1. > testdata <- data.frame(rating=mean(Affairs$rating),
  2.                          age=seq(17, 57, 10),
  3.                          yearsmarried=mean(Affairs$yearsmarried),
  4.                          religiousness=mean(Affairs$religiousness))
  5. > testdata
  6.   rating age yearsmarried religiousness
  7. 1   3.93  17         8.18          3.12
  8. 2   3.93  27         8.18          3.12
  9. 3   3.93  37         8.18          3.12
  10. 4   3.93  47         8.18          3.12
  11. 5   3.93  57         8.18          3.12
  13. > testdata$prob <- predict(fit.reduced, newdata=testdata, type="response")
  14. > testdata
  15.   rating age yearsmarried religiousness    prob
  16. 1   3.93  17         8.18          3.12   0.335
  17. 2   3.93  27         8.18          3.12   0.262
  18. 3   3.93  37         8.18          3.12   0.199
  19. 4   3.93  47         8.18          3.12   0.149
  20. 5   3.93  57         8.18          3.12   0.109

此处可以看到，当其他变量不变，年龄从17增加到57时，婚外情的概率将从0.34降低到0.11。利用该方法，你可探究每一个预测变量对结果概率的影响。

13.2.3　过度离势

抽样于二项分布的数据的期望方差是σ2 = nπ(1 - π)，n为观测数，π为属于Y = 1组的概率。所谓过度离势，即观测到的响应变量的方差大于期望的二项分布的方差。过度离势会导致奇异的标准误检验和不精确的显著性检验。

当出现过度离势时，仍可使用glm()函数拟合Logistic回归，但此时需要将二项分布改为类二项分布（quasibinomial distribution）。

检测过度离势的一种方法是比较二项分布模型的残差偏差与残差自由度，如果比值：

13.2　Logistic回归 - 图1

比1大很多，你便可认为存在过度离势。回到婚外情的例子，可得：

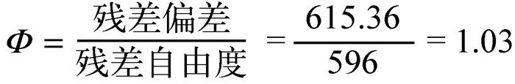
13.2　Logistic回归 - 图2

它非常接近于1，表明没有过度离势。

你还可以对过度离势进行检验。为此，你需要拟合模型两次，第一次使用family = "binomial"，第二次使用family = "quasibinomial"。假设第一次glm()返回对象记为fit，第二次返回对象记为fit.od，那么：

  1. pchisq(summary(fit.od)$dispersion * fit$df.residual,
  2.        fit$df.residual, lower = F)

提供的p值即可对零假设H0：Φ = 1 与备择假设H1：Φ ≠ 1进行检验。若p很小（小于0.05），你便可拒绝零假设。

将其应用到婚外情数据集，可得：

  1. > fit <- glm(ynaffair ~ age + yearsmarried + religiousness +
  2.              rating, family = binomial(), data = Affairs)
  3. > fit.od <- glm(ynaffair ~ age + yearsmarried + religiousness +
  4.                 rating, family = quasibinomial(), data = Affairs)
  5. > pchisq(summary(fit.od)$dispersion * fit$df.residual,
  6.          fit$df.residual, lower = F)
  8. [1] 0.34

此处p值（0.34）显然不显著（p > 0.05），这更增强了我们认为不存在过度离势的信心。下节介绍泊松回归时，我们仍将对过度离势问题进行讨论。

13.2.4　扩展

R中扩展的Logistic回归和变种如下所示。

  • 稳健Logistic回归　robust包中的glmRob()函数可用来拟合稳健的广义线性模型，包括稳健Logistic回归。当拟合Logistic回归模型数据出现离群点和强影响点时，稳健Logistic回归便可派上用场。

  • 多项分布回归　若响应变量包含两个以上的无序类别（比如，已婚/寡居/离婚），便可使用mlogit包中的mlogit()函数拟合多项Logistic回归。

  • 序数Logistic回归　若响应变量是一组有序的类别（比如，信用风险为差/良/好），便可使用rms包中的lrm()函数拟合序数Logistic回归。

可对多类别的响应变量（无论是否有序）进行建模是非常重要的扩展，但它也面临着解释性更复杂的困难。同时，在这种情况下评价模型拟合优度和回归诊断也变得更为复杂。

在婚外情的例子中，婚外偷腥的次数被二值化为一个“是/否”的响应变量，这是因为我们最感兴趣的是在过去一年中调查对象是否有过一次婚外情。如果兴趣转移到量上（过去一年中婚外情的次数），便可直接对计数型数据进行分析。分析计数型数据的一种流行方法是泊松回归，这便是我们接下来的话题。