9.7　多元方差分析

9.7　多元方差分析
- 9.7.1　评估假设检验
- 9.7.2　稳健多元方差分析

当因变量（结果变量）不止一个时，可用多元方差分析（MANOVA）对它们同时进行分析。以MASS包中的UScereal数据集为例[Venables，Ripley（1999）]，我们将研究美国谷物中的卡路里、脂肪和糖含量是否会因为储存架位置的不同而发生变化。其中1代表底层货架，2代表中层货架，3代表顶层货架。卡路里、脂肪和糖含量是因变量，货架是三水平（1、2、3）的自变量。分析过程见代码清单9-8。

代码清单9-8　单因素多元方差分析

> library(MASS)
> attach(UScereal)
> y <- cbind(calories, fat, sugars)
> aggregate(y, by=list(shelf), FUN=mean)
  Group.1 calories   fat sugars
1       1      119 0.662    6.3
2       2      130 1.341   12.5
3       3      180 1.945   10.9
> cov(y)
         calories   fat sugars
calories   3895.2 60.67 180.38
fat          60.7  2.71   4.00
sugars      180.4  4.00  34.05
> fit <- manova(y ~ shelf)
> summary(fit)
          Df Pillai approx F num Df den Df  Pr(>F)
shelf      1 0.1959   4.9550      3     61 0.00383 **
Residuals 63
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> summary.aov(fit)         # 输出单变量结果
 Response calories :
            Df  Sum Sq  Mean Sq  F value          Pr(>F)
shelf        1   45313   45313   13.995 0.0003983  ***
Residuals   63  203982    3238
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
 Response fat :
            Df   Sum Sq   Mean Sq  F value        Pr(>F)
shelf        1   18.421   18.421   7.476 0.008108  **
Residuals   63  155.236    2.464
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
 Response sugars :
            Df   Sum Sq   Mean Sq  F value       Pr(>F)
shelf        1   183.34   183.34   5.787 0.01909   *
Residuals   63  1995.87    31.68
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

代码清单9-8中，cbind()函数将三个因变量（卡路里、脂肪和糖）合并成一个矩阵。aggregate()函数可获取货架的各个均值，cov()则输出各谷物间的方差和协方差。

manova()函数能对组间差异进行多元检验。上面F值显著，说明三个组的营养成分测量值不同。

由于多元检验是显著的，因此可以使用summary.aov()函数对每一个变量做单因素方差分析。从上述结果可以看到，三组中每种营养成分的测量值都是不同的。另外，还可以用均值比较步骤（比如TukeyHSD）来判断对于每个因变量，哪种货架与其他货架都是不同的（此处已略去，以节省空间）。

9.7.1　评估假设检验

单因素多元方差分析有两个前提假设，一个是多元正态性，一个是方差—协方差矩阵同质性。

第一个假设即指因变量组合成的向量服从一个多元正态分布。可以用Q-Q图来检验该假设条件（参见补充内容“理论补充”对其工作原理的统计解释）。

理论补充

若有一个p*1的多元正态随机向量x，均值为μ，协方差矩阵为∑，那么x与μ的马氏距离的平方服从自由度为p的卡方分布。Q-Q图展示卡方分布的分位数，横纵坐标分别是样本量与马氏距离平方值。如果点全部落在斜率为1、截距项为0的直线上，则表明数据服从多元正态分布。

分析代码见代码清单9-9，结果见图9-11。

代码清单9-9　检验多元正态性

> center <- colMeans(y)
> n <- nrow(y)
> p <- ncol(y)
> cov <- cov(y)
> d <- mahalanobis(y,center,cov)
> coord <- qqplot(qchisq(ppoints(n),df=p),
    d, main="Q-Q Plot Assessing Multivariate Normality",
    ylab="Mahalanobis D2")
> abline(a=0,b=1)
> identify(coord$x, coord$y, labels=row.names(UScereal))

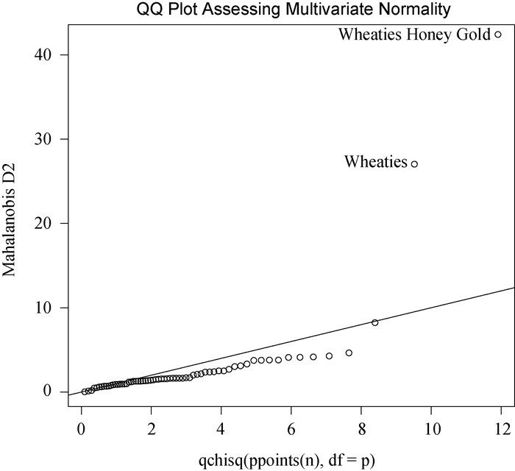
9.7　多元方差分析 - 图1

图9-11　检验多元正态性的Q-Q图

若数据服从多元正态分布，那么点将落在直线上。你能通过identify()函数（参见16.4节）交互性地对图中的点进行鉴别。从图形上看，观测点“Wheaties Honey Gold”和“Wheaties”异常，数据集似乎违反了多元正态性。可以删除这两个点再重新分析。

方差—协方差矩阵同质性即指各组的协方差矩阵相同，通常可用Box's M检验来评估该假设。由于R中没有Box's M函数，可以通过网络搜索找到合适的代码。另外，该检验对正态性假设很敏感，会导致在大部分案例中直接拒绝同质性假设。也就是说，对于这个重要的假设的检验，我们目前还没有一个好方法[但是可以参考Anderson（2006）和Silva et al.（2008）提供的一些有趣的备选方法，虽然在R中还没有实现]。

最后，还可以使用mvoutlier包中的ap.plot()函数来检验多元离群点。代码如下：

library(mvoutlier)
outliers <- aq.plot(y)
outliers

自己尝试一下，看看会得到什么结果吧！

9.7.2　稳健多元方差分析

如果多元正态性或者方差—协方差均值假设都不满足，又或者你担心多元离群点，那么可以考虑用稳健或非参数版本的MANOVA检验。稳健单因素MANOVA可通过rrcov包中的Wilks.test()函数实现。vegan包中的adonis()函数则提供了非参数MANOVA的等同形式。代码清单9-10是Wilks.test()的应用。

代码清单9-10　稳健单因素MANOVA

library(rrcov)
> Wilks.test(y,shelf,method="mcd")
        Robust One-way MANOVA (Bartlett Chi2)
data:  x
Wilks' Lambda = 0.511, Chi2-Value = 23.71, DF = 4.85, p-value =
0.0002143
sample estimates:
  calories   fat sugars
1      120 0.701   5.66
2      128 1.185  12.54
3      161 1.652  10.35

从结果来看，稳健检验对离群点和违反MANOVA假设的情况不敏感，而且再一次验证了存储在货架顶部、中部和底部的谷物营养成分含量不同。

9.7 多元方差分析