9.3　单因素方差分析

单因素方差分析中，你感兴趣的是比较分类因子定义的两个或多个组别中的因变量均值。以multcomp包中的cholesterol数据集为例（取自Westfall，Tobia，Rom，Hochberg，1999），50个患者均接受降低胆固醇药物治疗（trt）五种疗法中的一种疗法。其中三种治疗条件使用药物相同，分别是20 mg一天一次（1time）、10 mg一天两次（2times）和5 mg一天四次（4times）。剩下的两种方式（drugD和drugE）代表候选药物。哪种药物疗法降低胆固醇（响应变量）最多呢？分析过程见代码清单9-1。

代码清单9-1　单因素方差分析

  1. > library(multcomp)
  2. > attach(cholesterol)
  3. > table(trt)        # ❶ 各组样本大小
  4. trt
  5.  1time 2times 4times  drugD  drugE
  6.     10     10     10     10     10
  8. > aggregate(response, by=list(trt), FUN=mean)      # ❷ 各组均值
  9.   Group.1     x
  10. 1   1time  5.78
  11. 2  2times  9.22
  12. 3  4times 12.37
  13. 4   drugD 15.36
  14. 5   drugE 20.95
  16. > aggregate(response, by=list(trt), FUN=sd)      # ❸ 各组标准差
  17.   Group.1    x
  18. 1   1time 2.88
  19. 2  2times 3.48
  20. 3  4times 2.92
  21. 4   drugD 3.45
  22. 5   drugE 3.35
  24. > fit <- aov(response ~ trt)
  25. > summary(fit)         # ❹ 检验组间差异（ANOVA）
  26.             Df Sum Sq   Mean Sq    F value           Pr(>F)
  27. trt          4   1351       338       32.4     9.8e-13  ***
  28. Residuals   45    469        10
  29. ---
  30. Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  32. > library(gplots)
  33. > plotmeans(response ~ trt, xlab="Treatment", ylab="Response",     # ❺ 绘制各组均值及其置信区间的图形
  34.      main="Mean Plot\nwith 95% CI")
  35. > detach(cholesterol)

从输出结果可以看到，每10个患者接受其中一个药物疗法❶。均值显示drugE降低胆固醇最多，而1time降低胆固醇最少❷，各组的标准差相对恒定，在2.88到3.48间浮动❸。ANOVA对治疗方式（trt）的F检验非常显著（p<0.0001），说明五种疗法的效果不同❹。

gplots包中的plotmeans()可以用来绘制带有置信区间的组均值图形❺。如图9-1所示，图形展示了带有95%的置信区间的各疗法均值，可以清楚看到它们之间的差异。

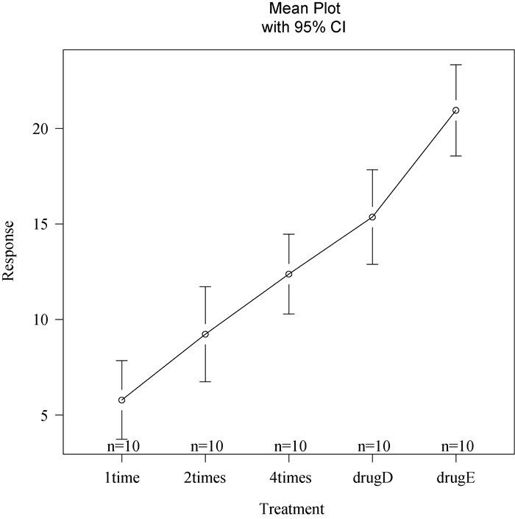
9.3　单因素方差分析 - 图1

图9-1　五种降低胆固醇药物疗法的均值，含95%的置信区间

9.3.1　多重比较

虽然ANOVA对各疗法的F检验表明五种药物疗法效果不同，但是并没有告诉你哪种疗法与其他疗法不同。多重比较可以解决这个问题。例如，TukeyHSD()函数提供了对各组均值差异的成对检验（见代码清单9-2）。但要注意TukeyHSD()函数与本章使用的HH包存在兼容性问题：若载入HH包，TukeyHSD()函数将会失效。对于上例，使用detach("package::HH")将它从搜寻路径中删除，然后再调用TukeyHSD()。

代码清单9-2　Tukey HSD的成对组间比较

  1. > TukeyHSD(fit)
  2.   Tukey multiple comparisons of means
  3.     95% family-wise confidence level
  5. Fit: aov(formula = response ~ trt)
  7. $trt
  8.                diff    lwr   upr p adj
  9. 2times-1time   3.44 -0.658  7.54 0.138
  10. 4times-1time   6.59  2.492 10.69 0.000
  11. drugD-1time    9.58  5.478 13.68 0.000
  12. drugE-1time   15.17 11.064 19.27 0.000
  13. 4times-2times  3.15 -0.951  7.25 0.205
  14. drugD-2times   6.14  2.035 10.24 0.001
  15. drugE-2times  11.72  7.621 15.82 0.000
  16. drugD-4times   2.99 -1.115  7.09 0.251
  17. drugE-4times   8.57  4.471 12.67 0.000
  18. drugE-drugD    5.59  1.485  9.69 0.003
  20. > par(las=2)
  21. > par(mar=c(5,8,4,2))
  22. > plot(TukeyHSD(fit))

可以看到，1time和2times的均值差异不显著（p=0.138），而1time和4times间的差异非常显著（p<0.001）。

成对比较图形如图9-2所示。第一个par语句用来旋转轴标签，第二个用来增大左边界的面积，可使标签摆放更美观（par选项参见第3章）。图形中置信区间包含0的疗法说明差异不显著（p>0.05）。

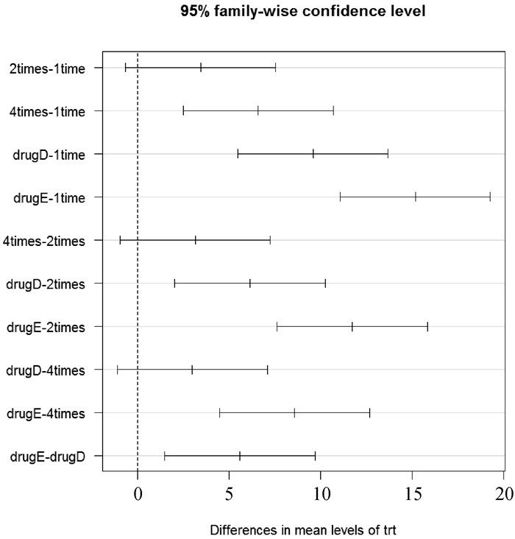
9.3　单因素方差分析 - 图2

图9-2　Tukey HSD均值成对比较图

multcomp包中的glht()函数提供了多重均值比较更为全面的方法，既适用于线性模型（如本章各例），也适用于广义线性模型（见第13章）。下面的代码重现了Tukey HSD检验，并用一个不同的图形对结果进行展示（图9-3）：

  1. > library(multcomp)
  2. > par(mar=c(5,4,6,2))
  3. > tuk <- glht(fit, linfct=mcp(trt="Tukey"))
  4. > plot(cld(tuk, level=.05),col="lightgrey")

上面的代码中，为适合字母阵列摆放，par语句增大了顶部边界面积。cld()函数中的level选项设置了使用的显著水平（0.05，即本例中的95%的置信区间）。

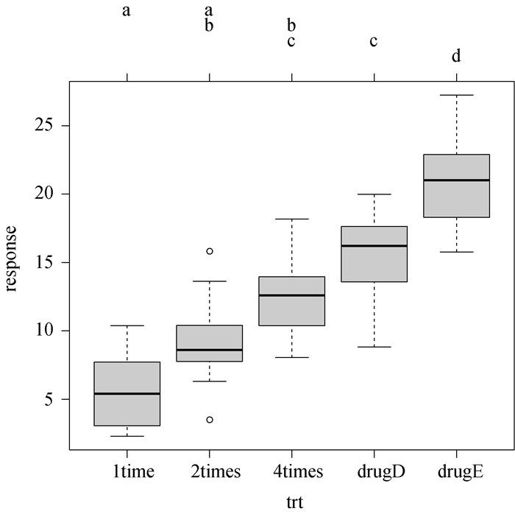
9.3　单因素方差分析 - 图3

图9-3　multcomp包中的Tukey HSD检验

有相同字母的组（用箱线图表示）说明均值差异不显著。可以看到，1time和2times差异不显著（有相同的字母a），2times和4times差异也不显著（有相同的字母b），而1time和4times差异显著（它们没有共同的字母）。个人认为，图9-3比图9-2更好理解，而且还提供了各组得分的分布信息。

从结果来看，使用降低胆固醇的药物时，一天四次5 mg剂量比一天一次20 mg剂量效果更佳，也优于候选药物drugD，但药物drugE比其他所有药物和疗法都更优。

多重比较方法是一个复杂但正迅速发展的领域，想了解更多，可参考Bretz、Hothorn和Westfall的Multiple Comparisons Using R（2010）一书。

9.3.2　评估检验的假设条件

上一章已经提过，我们对于结果的信心依赖于做统计检验时数据满足假设条件的程度。单因素方差分析中，我们假设因变量服从正态分布，各组方差相等。可以使用Q-Q图来检验正态性假设：

  1. > library(car)
  2. > qqPlot(lm(response ~ trt, data=cholesterol),
  3.          simulate=TRUE, main="Q-Q Plot", labels=FALSE)

注意qqPlot()要求用lm()拟合。图形如图9-4所示。

数据落在95%的置信区间范围内，说明满足正态性假设。

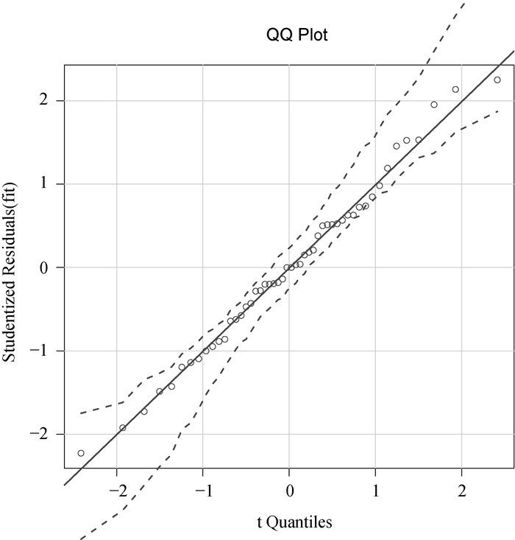
9.3　单因素方差分析 - 图4

图9-4　正态性检验

R提供了一些可用来做方差齐性检验的函数。例如，可以通过如下代码来做Bartlett检验：

  1. > bartlett.test(response ~ trt, data=cholesterol)
  3.         Bartlett test of homogeneity of variances
  5. data:  response by trt
  6. Bartlett's K-squared = 0.5797, df = 4, p-value = 0.9653

Bartlett检验表明五组的方差并没有显著不同（p=0.97）。其他检验如Fligner-Killeen检验（fligner.test()函数）和Brown-Forsythe检验（HH包中的hov()函数）此处没有做演示，但它们获得的结果与Bartlett检验相同。

不过，方差齐性分析对离群点非常敏感。可利用car包中的outlierTest()函数来检测离群点：

  1. > library(car)
  2. > outlierTest(fit)
  4. No Studentized residuals with Bonferonni p < 0.05
  5. Largest |rstudent|:
  6.    rstudent unadjusted p-value Bonferonni p
  7. 19 2.251149           0.029422           NA

从输出结果来看，并没有证据说明胆固醇数据中含有离群点（当p>1时将产生NA）。因此根据Q-Q图、Bartlett检验和离群点检验，该数据似乎可以用ANOVA模型拟合得很好。这些方法反过来增强了我们对于所得结果的信心。