9.6　重复测量方差分析

9.6　重复测量方差分析

所谓重复测量方差分析，即受试者被测量不止一次。本节重点关注含一个组内和一个组间因子的重复测量方差分析（这是一个常见的设计）。示例来源于生理生态学领域，研究方向是生命系统的生理和生化过程如何响应环境因素的变异（此为应对全球变暖的一个非常重要的研究领域）。基础安装包中的CO2数据集包含了北方和南方牧草类植物Echinochloa crus-galli （Potvin，Lechowicz，Tardif，1990）的寒冷容忍度研究结果，在某浓度二氧化碳的环境中，对寒带植物与非寒带植物的光合作用率进行了比较。研究所用植物一半来自于加拿大的魁北克省，另一半来自美国的密西西比州。

首先，我们关注寒带植物。因变量是二氧化碳吸收量（uptake），单位为ml/L，自变量是植物类型Type（魁北克VS密西西比州）和七种水平（95~1000 umol/m^2 sec）的二氧化碳浓度（conc）。另外，Type是组间因子，conc是组内因子。分析过程见代码清单9-7。

代码清单9-7　含一个组间因子和一个组内因子的重复测量方差分析

> w1b1 <- subset(CO2, Treatment=='chilled')
> fit <- aov(uptake ~ conc*Type + Error(Plant/(conc), w1b1)
> summary(fit)
Error: Plant
          Df  Sum Sq Mean Sq F value   Pr(>F)
Type       1 2667.24 2667.24  60.414 0.001477 **
Residuals  4  176.60   44.15
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Error: Plant:conc
          Df Sum Sq Mean Sq F value    Pr(>F)
conc       1 888.57  888.57  215.46 0.0001253 ***
conc:Type  1 239.24  239.24   58.01 0.0015952 **
Residuals  4  16.50    4.12
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Error: Within
          Df Sum Sq Mean Sq F value Pr(>F)
Residuals 30 869.05   28.97
> par(las=2)
> par(mar=c(10,4,4,2))
> with(w1b1, interaction.plot(conc,Type,uptake,
       type="b", col=c("red","blue"), pch=c(16,18),
       main="Interaction Plot for Plant Type and Concentration"))
> boxplot(uptake ~ Type*conc, data=w1b1, col=(c("gold", "green")),
         main=”Chilled Quebec and Mississippi Plants”,
          ylab=”Carbon dioxide uptake rate (umol/m^2 sec)”)

方差分析表表明在0.01的水平下，主效应类型和浓度以及交叉效应类型x浓度都非常显著，图9-9中通过interaction.plot()函数展示了交互效应。

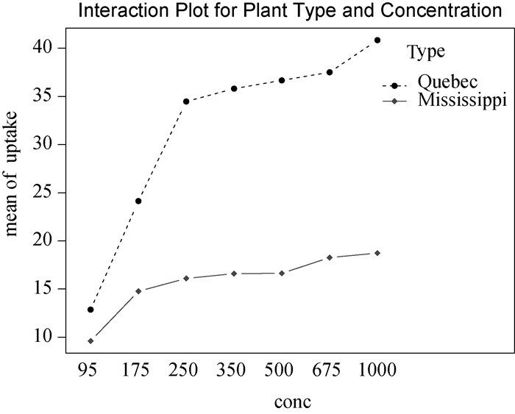
9.6　重复测量方差分析 - 图1

图9-9　CO₂浓度和植物类型对CO₂吸收的交互影响。图形由interaction.plot()函数绘制

若想展示交互效应其他不同的侧面，可以使用boxplot()函数对相同的数据画图，结果见图9-10。

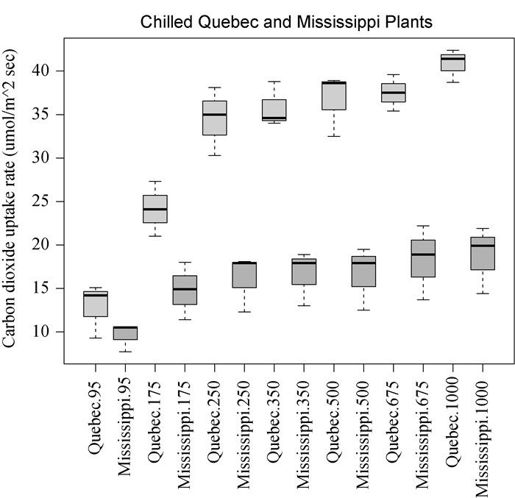
9.6　重复测量方差分析 - 图2

图9-10　CO₂浓度和植物类型对CO₂吸收的交互效应。图形由boxplot()函数绘制

从以上任意一幅图都可以看出，魁北克省的植物比密西西比州的植物二氧化碳吸收率高，而且随着CO₂浓度的升高，差异越来越明显。

注意　通常处理的数据集是宽格式（wide format），即列是变量，行是观测值，而且一行一个受试对象。9.4节中的litter数据框就是一个很好的例子。不过在处理重复测量设计时，需要有长格式（long format）数据才能拟合模型。在长格式中，因变量的每次测量都要放到它独有的行中，CO2数据集即该种形式。幸运的是，5.6.3节的reshape包可方便地将数据转换为相应的格式。

混合模型设计的各种方法

在分析本节关于CO₂的例子时，我们使用了传统的重复测量方差分析。该方法假设任意组内因子的协方差矩阵为球形，并且任意组内因子两水平间的方差之差都相等。但在现实中这种假设不可能满足，于是衍生了一系列备选方法：

使用lme4包中的lmer()函数拟合线性混合模型（Bates，2005）；

使用car包中的Anova()函数调整传统检验统计量以弥补球形假设的不满足（例如Geisser-Greenhouse校正）；

使用nlme包中的gls()函数拟合给定方差-协方差结构的广义最小二乘模型（UCLA，2009）；

用多元方差分析对重复测量数据进行建模（Hand，1987）。

以上方法已超出本书范畴，如果你对这些方法感兴趣，可以参考Pinheiro & Bates（2000）、 Zuur et al.（2009）。

目前为止，本章都只是对单个因变量的情况进行分析，在下一节，我们将简略介绍多个结果变量的设计。

9.6 重复测量方差分析