8.6　选择“最佳”的回归模型

尝试获取一个回归方程时，实际上你就面对着从众多可能的模型中做选择的问题。是不是所有的变量都要包括？抑或去掉那个对预测贡献不显著的变量？还是需要添加多项式项和/或交互项来提高拟合度？最终回归模型的选择总是会涉及预测精度（模型尽可能地拟合数据）与模型简洁度（一个简单且能复制的模型）的调和问题。如果有两个几乎相同预测精度的模型，你肯定喜欢简单的那个。本节讨论的问题，就是如何在候选模型中进行筛选。注意，“最佳”是打了引号的，因为没有做评价的唯一标准，最终的决定需要调查者的评判。（把它看做工作保障吧。）

8.6.1　模型比较

用基础安装中的anova()函数可以比较两个嵌套模型的拟合优度。所谓嵌套模型，即它的一些项完全包含在另一个模型中。在states的多元回归模型中，我们发现Income和Frost的回归系数不显著，此时你可以检验不含这两个变量的模型与包含这两项的模型预测效果是否一样好（见代码清单8-11）。

代码清单8-11　用anova()函数比较

  1. > fit1 <- lm(Murder ~ Population + Illiteracy + Income + Frost,
  2.           data=states)
  3. > fit2 <- lm(Murder ~ Population + Illiteracy, data=states)
  4. > anova(fit2, fit1)
  6. Analysis of Variance Table
  8. Model 1: Murder ~ Population + Illiteracy
  9. Model 2: Murder ~ Population + Illiteracy + Income + Frost
  10.   Res.Df     RSS  Df     Sum of Sq      F Pr(>F)
  11. 1     47 289.246
  12. 2     45 289.167  2     0.079 0.0061     0.994

此处，模型1嵌套在模型2中。anova()函数同时还对是否应该添加Income和Frost到线性模型中进行了检验。由于检验不显著（p=0.994），因此我们可以得出结论：不需要将这两个变量添加到线性模型中，可以将它们从模型中删除。

AIC（Akaike Information Criterion，赤池信息准则）也可以用来比较模型，它考虑了模型的统计拟合度以及用来拟合的参数数目。AIC值越小的模型要优先选择，它说明模型用较少的参数获得了足够的拟合度。该准则可用AIC()函数实现（见代码清单8-12）。

代码清单8-12　用AIC来比较模型

  1. > fit1 <- lm(Murder ~ Population + Illiteracy + Income + Frost,
  2.           data=states)
  3. > fit2 <- lm(Murder ~ Population + Illiteracy, data=states)
  4. > AIC(fit1,fit2)
  6.      df      AIC
  7. fit1  6 241.6429
  8. fit2  4 237.6565

此处AIC值表明没有Income和Frost的模型更佳。注意，ANOVA需要嵌套模型，而AIC方法不需要。

比较两模型相对来说更为直接，但如果有4个、10个，或者100个可能的模型怎么办呢？这便是下节的主题。

8.6.2　变量选择

从大量候选变量中选择最终的预测变量有以下两种流行的方法：逐步回归法（stepwise method）和全子集回归（all-subsets regression）。

  • 逐步回归

逐步回归中，模型会一次添加或者删除一个变量，直到达到某个判停准则为止。例如，向前逐步回归（forward stepwise）每次添加一个预测变量到模型中，直到添加变量不会使模型有所改进为止。向后逐步回归（backward stepwise）从模型包含所有预测变量开始，一次删除一个变量直到会降低模型质量为止。而向前向后逐步回归（stepwise stepwise，通常称作逐步回归，以避免听起来太冗长），结合了向前逐步回归和向后逐步回归的方法，变量每次进入一个，但是每一步中，变量都会被重新评价，对模型没有贡献的变量将会被删除，预测变量可能会被添加、删除好几次，直到获得最优模型为止。

逐步回归法的实现依据增删变量的准则不同而不同。MASS包中的stepAIC()函数可以实现逐步回归模型（向前、向后和向前向后），依据的是精确AIC准则。代码清单8-13中，我们应用的是向后回归。

代码清单8-13　向后回归

  1. > library(MASS)
  2. > fit1 <- lm(Murder ~ Population + Illiteracy + Income + Frost,
  3.           data=states)
  4. > stepAIC(fit, direction="backward")
  5. 　
  6. Start:  AIC=97.75
  7. Murder ~ Population + Illiteracy + Income + Frost
  8. 　
  9.              Df Sum of Sq    RSS    AIC
  10. - Frost       1      0.02 289.19  95.75
  11. - Income      1      0.06 289.22  95.76
  12. <none>                    289.17  97.75
  13. - Population  1     39.24 328.41 102.11
  14. - Illiteracy  1    144.26 433.43 115.99
  15. 　
  16. Step:  AIC=95.75
  17. Murder ~ Population + Illiteracy + Income
  18. 　
  19.              Df Sum of Sq    RSS    AIC
  20. - Income      1       0.06 289.25 93.76
  21. <none>                     289.19 95.75
  22. - Population  1     43.66 332.85 100.78
  23. - Illiteracy  1    236.20 525.38 123.61
  24. 　
  25. Step:  AIC=93.76
  26. Murder ~ Population + Illiteracy
  27. 　
  28.              Df Sum of Sq    RSS    AIC
  29. <none>                    289.25  93.76
  30. - Population  1     48.52 337.76  99.52
  31. - Illiteracy  1    299.65 588.89 127.31
  32. 　
  33. Call:
  34. lm(formula=Murder ~ Population + Illiteracy, data=states)
  35. 　
  36. Coefficients:
  37. (Intercept)   Population   Illiteracy
  38.   1.6515497    0.0002242    4.0807366

开始时模型包含4个（全部）预测变量，然后每一步中，AIC列提供了删除一个行中变量后模型的AIC值，中的AIC值表示没有变量被删除时模型的AIC。第一步，Frost被删除，AIC从97.75降低到95.75；第二步，Income被删除，AIC继续下降，成为93.76，然后再删除变量将会增加AIC，因此终止选择过程。

逐步回归法其实存在争议，虽然它可能会找到一个好的模型，但是不能保证模型就是最佳模型，因为不是每一个可能的模型都被评价了。为克服这个限制，便有了全子集回归法。

  • 全子集回归

全子集回归，顾名思义，即所有可能的模型都会被检验。分析员可以选择展示所有可能的结果，也可以展示n 个不同子集大小（一个、两个或多个预测变量）的最佳模型。例如，若nbest=2，先展示两个最佳的单预测变量模型，然后展示两个最佳的双预测变量模型，以此类推，直到包含所有的预测变量。

全子集回归可用leaps包中的regsubsets()函数实现。你能通过R平方、调整R平方或Mallows Cp统计量等准则来选择“最佳”模型。

R平方含义是预测变量解释响应变量的程度；调整R平方与之类似，但考虑了模型的参数数目。R平方总会随着变量数目的增加而增加。当与样本量相比，预测变量数目很大时，容易导致过拟合。R平方很可能会丢失数据的偶然变异信息，而调整R平方则提供了更为真实的R平方估计。另外，Mallows Cp统计量也用来作为逐步回归的判停规则。广泛研究表明，对于一个好的模型，它的Cp统计量非常接近于模型的参数数目（包括截距项）。

在代码清单8-14中，我们对states数据进行了全子集回归。结果可用leaps包中的plot()函数绘制（如图8-17所示），或者用car包中的subsets()函数绘制（如图8-18所示）。

代码清单8-14　全子集回归

  1. library(leaps)
  2. leaps <-regsubsets(Murder ~ Population + Illiteracy + Income +
  3.   Frost, data=states, nbest=4)
  4. plot(leaps, scale="adjr2")
  5. 　
  6. library(car)
  7. subsets(leaps, statistic="cp",
  8.   main="Cp Plot for All Subsets Regression")
  9. abline(1,1,lty=2,col="red")

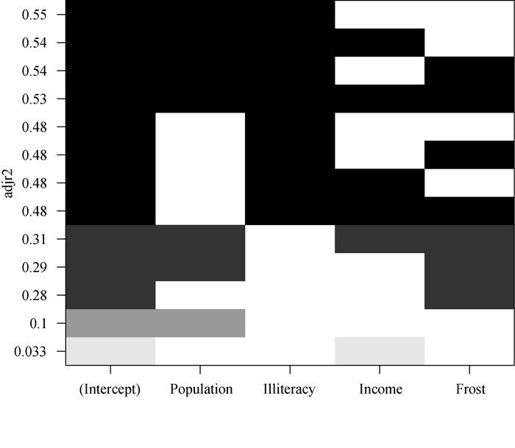
8.6　选择“最佳”的回归模型 - 图1

图8-17　基于调整R平方，不同子集大小的四个最佳模型

初看图8-17可能比较费解。第一行中（图底部开始），可以看到含intercept（截距项）和Income的模型调整R平方为0.33，含intercept和Population的模型调整R平方为0.1。跳至第12行，你会看到含intercept、Population、Illiteracy和Income的模型调整R平方值为0.54，而仅含intercept、Population和Illiteracy的模型调整R平方为0.55。此处，你会发现含预测变量越少的模型调整R平方越大（对于非调整的R平方，这是不可能的）。图形表明，双预测变量模型（Population和Illiteracy）是最佳模型。

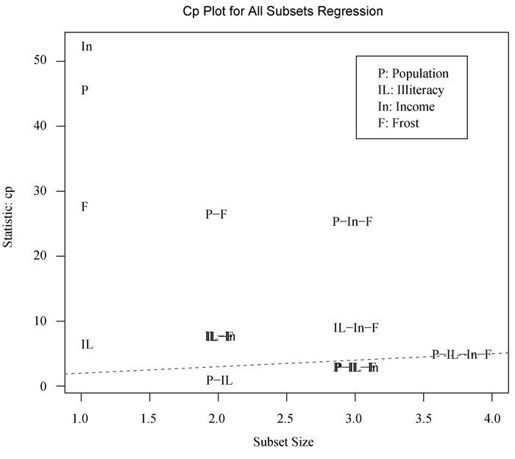
8.6　选择“最佳”的回归模型 - 图2

图8-18　基于Mallows Cp统计量，不同子集大小的四个最佳模型

在图8-18中，你会看到对于不同子集大小，基于Mallows Cp统计量的四个最佳模型。越好的模型离截距项和斜率均为1的直线越近。图形表明，你可以选择这几个模型，其余可能的模型都可以不予考虑：含Population和Illiteracy的双变量模型；含Population、Illiteracy和Frost的三变量模型，或Population、Illiteracy和Income的三变量模型（它们在图形上重叠了，不易分辨）；含Population、Illiteracy、Income和Frost的四变量模型。

大部分情况中，全子集回归要优于逐步回归，因为考虑了更多模型。但是，当有大量预测变量时，全子集回归会很慢。一般来说，变量自动选择应该被看做是对模型选择的一种辅助方法，而不是直接方法。拟合效果佳而没有意义的模型对你毫无帮助，主题背景知识的理解才能最终指引你获得理想的模型。