1.3　自动控制系统分类

自动控制系统广泛应用于各类工业部门。随着生产规模的不断扩大和生产能力的不断提高，以及自动化技术和控制理论的发展，自动控制系统也日益复杂和日趋完善。例如，由单输入单输出的控制系统发展为多输入多输出的系统；由具有常规控制仪表和控制器的连续控制系统，发展到由计算机作为控制器的直接数字控制系统，从而实现最优控制。由于各式各样自动控制系统的不断发展，很难确切地对自动控制系统进行分类。现将常见的几种自动控制系统概括介绍如下。

1.3.1　线性系统和非线性系统

按不同系统的特征方程式，可将自动控制系统分为线性系统和非线性系统。

线性控制系统是由线性元件组成的系统，该系统的特征方程式可以用线性微分方程描述。叠加性和齐次性是鉴别系统是否为线性系统的根据。线性微分方程的各项系数为常数时，称为线性定常系统。线性定常系统可以用拉普拉斯变换解微分方程，并由此定义出系统传递函数这一系统动态数学模型。根轨迹法和频率法就是在这一基础上发展起来的分析和设计线性系统的有效方法。多输入多输出系统所采用的状态空间、传递矩阵等分析方法，将在有关章节中论述。

如果系统微分方程的系数与自变量有关，则为非线性微分方程，由非线性微分方程描述的系统称为非线性控制系统。在自动控制系统中，即使只含一个非线性环节，这一系统也是非线性的。

对于非线性控制系统的理论与研究远不如线性控制系统那样完整，一般只能满足于近似的定性描述和数值计算。任何物理系统的特性，精确地说都是非线性的，但在误差允许范围内，可以将非线性特性线性化，近似地用线性微分方程来描述，这样就可以按照线性系统来处理。

非线性系统的暂态特性与其初始条件有关，从这一点来看，它与线性系统有很大的区别。例如当偏差的初始值很小时，系统的暂态过程是稳定的，而当偏差量的初值较大时，则可能不稳定。线性系统的暂态过程与初始条件无关。

1.3.2　离散系统和连续系统

从数学模型角度而言，连续系统各部分信号均以模拟的连续函数形式表示，以前的大部分闭环系统都属于连续系统。

从数学模型角度而言，离散系统的某一处或几处信号是以脉冲序列或数字形式表示的。目前的计算机控制系统都属于离散系统。

离散系统的主要特点是：在系统中使用脉冲开关或采样开关，将连续信号转变为离散信号。通常对以离散信号取脉冲形式的系统，称为脉冲控制系统；而对于采样数字计算机或数字控制器，其离散信号以数字形式传递的系统称为采样数字控制系统。图1.4是典型的采样数字控制系统结构示意图。

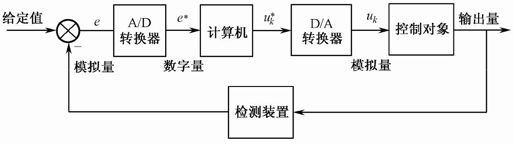
图1.4　采样数字控制系统结构示意图

由于被控对象的输入量和输出量是模拟信号，而计算机的输入量和输出量是数字信号，所以要有将模拟量转换为数字量的模/数转换装置（A/D）和把数字量转换为模拟量的数/模转换装置（D/A）。

研究离散系统的方法和研究连续系统的方法类似。

1.3.3　恒值系统和随动系统

在现代生产应用中使用最多的闭环自动控制系统，按给定量的不同特征，可将系统分为恒值系统和随动系统。

恒值系统往往要求被控制量保持在恒定值，其给定量是不变的，如恒温、恒速、恒压等自动控制系统。

在随动系统中，给定量是按照事先不知道的时间函数变化，要求输出量跟随给定量的变化而变化，因此也称为同步随动系统，如自动火炮的控制系统。