9.5　综合实例及MATLAB/Simulink应用

9.5　综合实例及MATLAB/Simulink应用

下面通过一个综合实例，讲述MATLAB/Simulink在本章中的应用。

【例9-13】　给定如下线性定常系统：

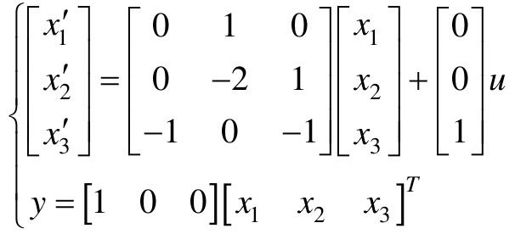
P_280-1

试利用MATLAB进行以下分析：

（1）分析系统的可控性、可观性；

（2）对系统进行非奇异线性变换，使其状态转移矩阵对角化，进而分析变换后系统的可控性、可观性；

（3）分析系统的稳定性，绘制系统的阶跃响应曲线；

（4）使用LTI Viewer工具绘制上述系统的阶跃响应和冲激响应曲线。

解：利用MATLAB求解的基本步骤如下。

【步骤1】　建立控制系统的数学模型。

题设中的系统采用状态空间的方式给出，所以建模时需要利用ss()命令，相应的MATLAB代码如下：

clear all;        %清除工作空间的变量
A = [0 1 0; 0 -2 1; -1 0 -1];  B = [0;0;1];  C = [1 0 0]; D = 0;
sys = ss(A,B,C,D)       %利用ss()命令建立状态空间模型

程序运行后，在MATLAB工作空间建立系统的状态空间模型。

【步骤2】　检验此系统的可控性和可观性。

相应的MATLAB代码如下：

control_matrix = ctrb(A,B);     %检验控制系统的可控性
rank_control = rank(control_matrix);
if rank_control < 3        %根据题意，可知能控矩阵的秩小于3时，系统不可控
    disp('系统不可控!');
else
    disp('系统可控!');
end
observe_matrix = obsv(A,C);     %检验控制系统的可观性
rank_observe = rank(observe_matrix);
if rank_observe < 3         %根据题意，可知能观矩阵的秩小于3时，系统可观
    disp('系统不可观!');
else
    disp('系统可观!');
end

程序的运行结果为：

系统可控！
系统可观！

可见，题目中给定的系统是完成能控能观的。

【步骤3】　对系统进行线性对角化变换。

需要利用求取矩阵特征值和特征向量的命令eig()，相应的MATLAB代码如下：

[V,S] = eig(A)       %求取矩阵特征值和特征向量
if rank(V) == 3       %矩阵满秩，进行对角化变换
    AA = inv(V) * A * V;
    BB = inv(V) * B;
    CC = C * V;
    sys_diag = ss(AA,BB,CC,D)
else
    disp('这个系统不可对角化');
end

程序运行结果为：

a =                x1                    x2                    x3
   x1         -0.338+0.562i  1.39e-017-4.16e-016i  2.64e-016+4.23e-016i
   x2  1.39e-017+4.72e-016i         -0.338-0.562i  1.39e-017-6.66e-01
   x3     1e-016+1.49e-016i  1.22e-016-1.29e-016i      -2.32+7.91e-01
b =           u1
   x1       0.593+0.398i
   x2       0.593-0.398i
   x3  -0.619+4.55e-017i
c =          x1            x2            x3
   y1  -0.459-0.39i  -0.459+0.39i        -0.379
d =     u1
   y1   0

由于数值计算的精度问题，上面的结果中矩阵a、b、c实际应为

P_282-1

不难看出，此时系统的状态矩阵确实为对角矩阵。

【步骤4】　分析线性变换后的系统可控性及可观性。

相应的MATLAB代码如下：

control_matrix = ctrb(AA,BB);    %检验控制系统的可控性
rank_control = rank(control_matrix);
if rank_control < 3       %根据题意，可知能控矩阵的秩小于3时，系统不可控
    disp('线性变换后系统不可控！');
else
    disp('线性变换后系统可控！');
end
observe_matrix = obsv(AA,CC);    %检验控制系统的可观性
rank_observe = rank(observe_matrix);
if rank_observe < 3      %根据题意，可知能观矩阵的秩小于3时，系统可观
    disp('线性变换后系统不可观！');
else
    disp('线性变换后系统可观！');
end

程序运行结果为：

线性变换后系统可控！
线性变换后系统可观！

这也验证了“对系统进行非奇异线性变换，不改变其原有的可控性和可观性”。

【步骤5】　分析系统的稳定性。

利用李雅普诺夫方法，分析系统的稳定性，相应的MATLAB代码如下：

P = lyap(A',eye(3))        %利用李雅普诺夫方法分析系统的稳定性

程序运行的结果为：

P = 3.5000    1.5000    0.5000
    1.5000    1.0000    0.5000
    0.5000    0.5000    1.0000

不难看出，P矩阵为正定的，因此系统是渐进稳定的。

【步骤6】　绘制系统的阶跃响应曲线。

相应的MATLAB代码如下：

step(sys)         %绘制阶跃响应曲线

运行程序，输出结果如图9.17所示。

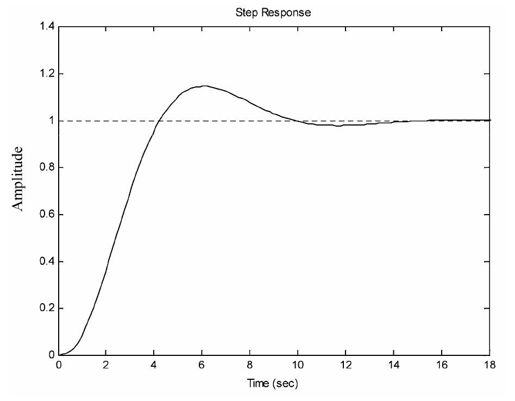
P_283-1

图9.17　系统的阶跃响应曲线

曲线收敛，验证了（4）中得出的结论：系统渐进稳定，因此这是一个既可控、又可观的渐进稳定线性定常系统。

【步骤7】　使用LTI Viewer工具进行分析。

用LTI Viewer工具绘制上述系统的阶跃响应曲线。代码如下：

ltiview;          % 调用LTI Viewer工具

在LTI Viewer工具中，导入控制系统模型sys，并且选择Plot Configurations，同时绘制系统sys的阶跃响应曲线和冲激响应曲线，结果如图9.18所示。

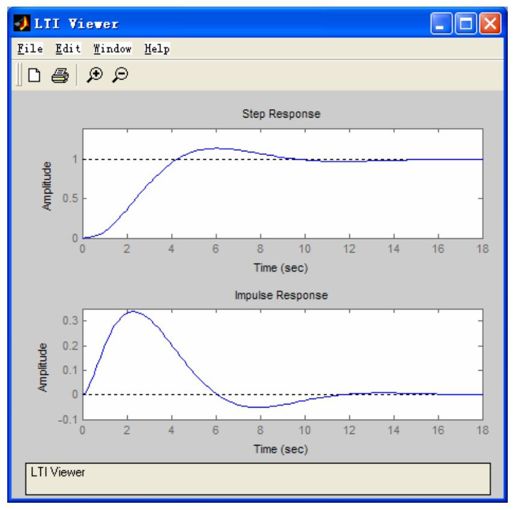
P_284-1

图9.18　用LTI Viewer工具进行线性系统的状态空间分析

从图9.18中不难看出，题设中的线性系统是渐进稳定的。这与步骤5得出的结论是完全一致的。

习　题

【9.1】　已知系统的状态方程如下：

P_284-2

（1）利用MATLAB建立控制系统的数学模型；

（2）编程绘制上述系统的阶跃响应和冲激响应，并分析系统稳定性；

（3）练习使用LTI Viewer工具，绘制系统的阶跃响应曲线和冲激响应曲线；

（4）计算上述系统的能控矩阵和能观矩阵，给出系统的能控性和能观性。

【9.2】　将如下几个系统化为特征值规范型。

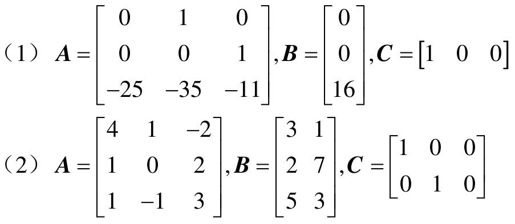
P_284-3

【9.3】　给定系统的状态方程如下：

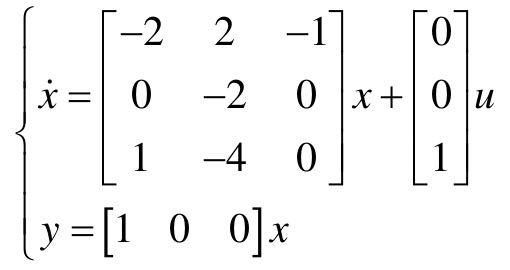
P_284-4

（1）利用MATLAB建立控制系统的数学模型；

（2）分析系统的可控性和可观性；

（3）计算系统的传递函数；

（4）根据传递函数，计算系统的零极点，并判断系统的稳定性；

（5）利用LTI Viewer工具绘制系统的阶跃响应曲线，验证系统的稳定性。

【9.4】　判断如下系统的可控子空间维数（可控子空间维数等于可控性矩阵的秩）。

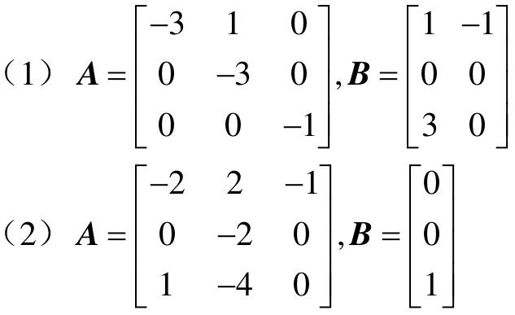
P_285-1

【9.5】　判断如下系统的可观子空间维数（可观子空间维数等于可观性矩阵的秩）。

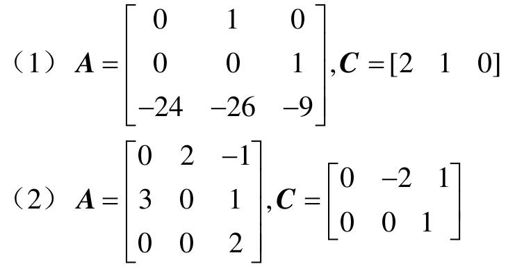
P_285-2

【9.6】　给定系统

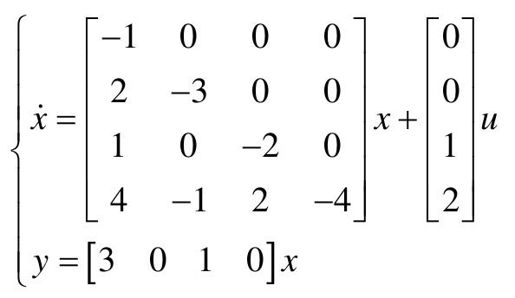
P_285-3

（1）利用MATLAB建立控制系统的数学模型；

（2）判断系统的可控性和可观性；如果不是完全可控或完全可观的，则计算其可控子空间维数和可观子空间维数；

（3）计算上述系统的传递函数；

（4）根据得到的传递函数，计算系统的零极点，判断系统的稳定性；

（5）在LTI Viewer中，绘制系统的阶跃响应曲线，验证系统的稳定性；

（6）利用李雅普诺夫方法，判断系统的稳定性，分析结果是否与第（4）问吻合。

9.5 综合实例及MATLAB/Simulink应用