5.5 综合实例及MATLAB/Simulink应用
下面通过两个综合实例,讲述MATLAB/Simulink在本章中的应用。
【例5-18】 某随动系统的结构如图5.43所示。利用MATLAB完成如下工作:
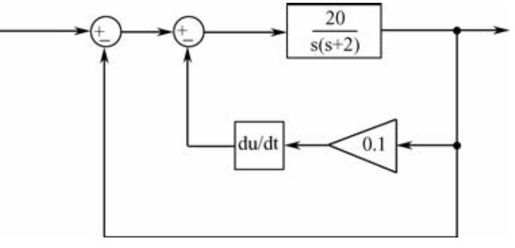
图5.43 随动系统的结构图
(1)对给定的随动系统建立数学模型;
(2)分析系统的稳定性,并且绘制阶跃响应曲线;
(3)计算系统的稳态误差;
(4)大致分析系统的总体性能,并给出理论上的解释。
解:利用MATLAB求解的基本步骤如下。
【步骤1】 求取系统的传递函数。
首先需要对系统框图进行化简。不难看出,题目中给出的系统包含两级反馈:外环是单位负反馈;内环则是二阶系统与微分环节构成的负反馈。可以利用MATLAB中的feedback函数计算出系统的传递函数。代码如下:
- clc; % 清除屏幕显示
- clear all; % 清除工作空间中的所有变量
- num1 = [20]; den1 = [1 2 0]; % 传递函数的分子、分母多项式系数
- sys1 = tf(num1,den1); % 二阶系统的传递函数
- num2 = [0.1 0]; den2 = [0 1]; % 微分环节传递函数的分子、分母多项式系数
- sys2 = tf(num2,den2); % 微分环节的传递函数
- sys_inner = feedback( sys1, sys2 ); % 内环反馈的传递函数
- sys_outer = feedback( sys_inner,1 ) % 外环反馈的传递函数
程序运行的结果为:
- Transfer function:
- 20
- -----------------
- s^2 + 4 s + 20
这样,就得出了系统的总体传递函数,即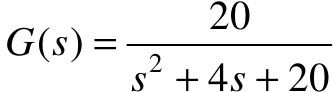 。
。
【步骤2】 进行稳定性分析。
根据求得的传递函数,对系统进行稳定性分析。可以采用roots命令求出传递函数分母多项式的根(即系统的极点),判断其实部是否都为负值;还可以利用pzmap直接绘制出系统的零极点,观察其分布。代码如下:
- % 根据求得的系统传递函数,利用 roots 命令判断系统的稳定性
- den = [1 4 20]; % 闭环系统传递函数分母多项式系数
- roots(den) % 求闭环系统特征多项式的根
- pzmap(sys_outer); % 利用 pzmap 命令绘制系统的零极点图
- grid on; % 在图像中显示网格线
程序运行的结果如下:
- ans = -2.0000 + 4.0000i
- -2.0000 - 4.0000i
可见,系统特征根均具有负实部,因此闭环系统是稳定的。
系统的零极点分布如图5.44所示。
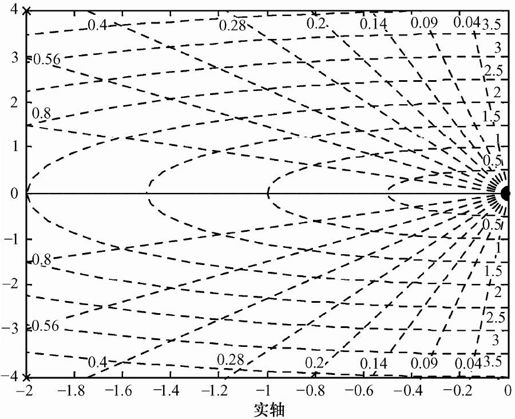
图5.44 系统的零极点分布图
从图中也不难看出,极点(在图中用“×”标识)都在左半平面,系统稳定。这与用roots命令得出的结论完全相同。在实际应用中,采用pzmap更为形象,而且代码更加简单。
【步骤3】 求取阶跃响应。
计算系统的阶跃响应:可以采用MATLAB编程实现,还可以利用Simulink对系统进行建模,直接观察响应曲线。MATLAB程序代码如下:
- % 计算系统的阶跃响应
- num = [20]; den = [1 4 20]; % 闭环系统传递函数分子、分母多项式系数
- [y,t,x] = step(num,den) % 计算闭环系统的阶跃响应
- plot(x,y); % 绘制阶跃响应曲线
- grid on; % 在图像中显示网格线
程序运行的结果如图5.45所示。其中,横坐标表示响应时间,纵坐标表示系统输出。
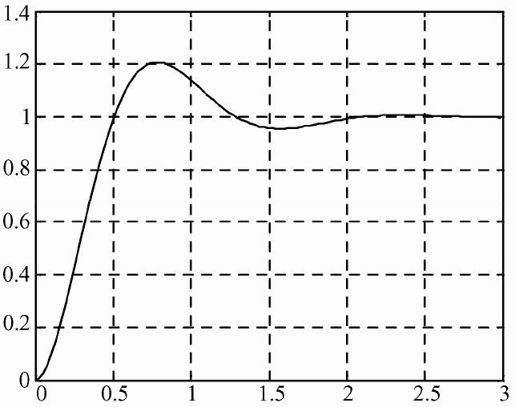
图5.45 系统阶跃响应曲线
采用Simulink对系统进行建模,如图5.46所示。其中,示波器Scope用来观察系统的响应曲线;示波器error用来观察系统的误差曲线。这里放置了3个信号源:阶跃信号、速度信号及加速度信号。选择不同的信号源,可以从Scope中得到系统的不同响应曲线。
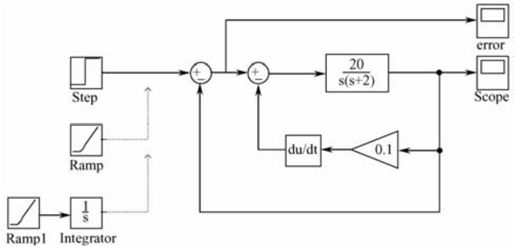
图5.46 利用Simulink对系统建模
用step信号激励系统,得到的输出如图5.47所示。
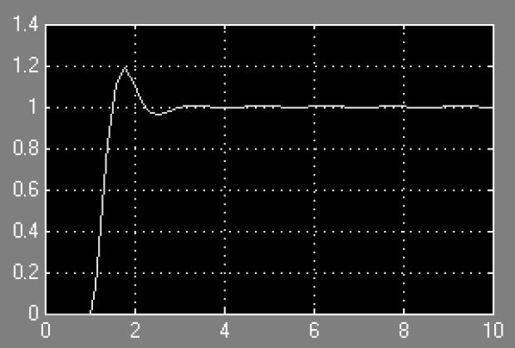
图5.47 系统阶跃响应曲线
这与编程得到的结果是完全相同的。
【步骤4】 分析系统的响应特性。
在上面的语句[y,t,x]=step(num,den)执行之后,变量y中就存放了系统阶跃响应的具体数值。从响应曲线中不难看出,系统的稳态值为1。可以利用如下代码计算系统的超调量:
- % 计算系统的超调量
- y_stable = 1; % 阶跃响应的稳态值
- max_response = max(y); % 闭环系统阶跃响应的最大值
- sigma = ( max_response - y_stable ) / y_stable % 阶跃响应的超调量
程序运行的结果为:
- sigma = 0.2076
同时可看出,系统的稳态误差为0。示波器error的波形显示如图5.48所示。
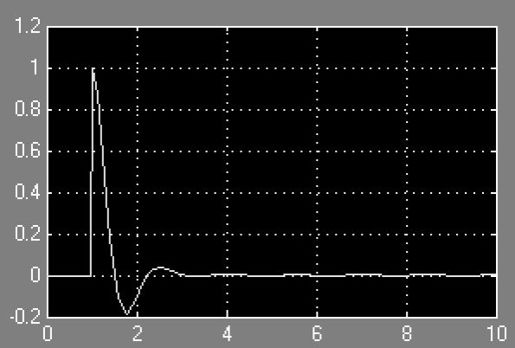
图5.48 系统误差曲线
可见,当阶跃输入作用系统2 s之后,输出就基本为1了。
还可以精确计算出系统的上升时间、峰值时间及调整时间。如上所述,y中存储了系统阶跃响应的数据;同时,x中存放了其中每个数据对应的时间。编写代码如下:
- % 计算系统的上升时间
- for i = 1 : length(y) % 遍历响应曲线
- if y(i) > y_stable % 如果某个时刻系统的输出值大于稳态值
- break; % 循环中断
- end
- end
- tr = x(i) % 计算此时对应的时间,就是阶跃响应的上升时间
- % 计算系统的峰值时间
- [max_response, index] = max(y); % 查找系统阶跃响应的最大值
- tp = x(index) % 计算此时对应的时间,就是阶跃响应的峰值时间
- % 计算系统的调整时间 ---> 取误差带为 2%
- for i = 1 : length(y) % 遍历响应曲线
- if max(y(i:length(y))) <= 1.02 * y_stable % 如果当前响应值在误差带内
- if min(y(i:length(y))) >= 0.98 * y_stable
- break; % 循环退出
- end
- end
- end
- ts = x(i) % 计算此时对应的时间,就是系统阶跃响应的调整时间
程序运行的结果如下:
- tr = 0.5245
- tp = 0.7730
- ts = 1.8773
即上升时间为0.52 s,峰值时间为0.77 s,并且系统在经过1.88 s后进入稳态。
综合利用MATLAB编程和Simulink仿真,可以很方便地对系统的响应性能进行分析。
【例5-19】已知某二阶系统的传递函数为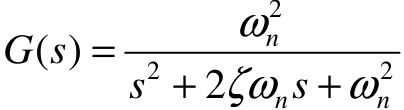 ,
,
(1)将自然频率固定为ωn=1, ζ=0,0.1,…,1,2,3,5,分析ζ变化时系统的单位阶跃响应;
(2)将阻尼比ζ固定为ζ=0.55,分析自然频率ωn变化时系统的单位阶跃响应(ωn的变化范围为0.1~1)。
解:利用MATLAB建立控制系统的数学模型,并且同时显示ωn=1,ζ(阻尼系数)取不同值时系统的阶跃响应曲线,代码如下:
- clc; % 清除屏幕显示
- clear; % 清除工作空间中的所有变量
- t = linspace(0,20,200)'; % 设置仿真时间
- omega = 1; % 设置二阶系统的自然频率
- omega2 = omega^2; % 计算自然频率的平方
- zuni = [0, 0.1, 0.2, 0.5, 1, 2, 3, 5]; % 设置阻尼系数向量
- num = omega2; % 二阶系统传递函数的分子多项式系数
- for k = 1 : 8 % 循环8次,分别计算在8种不同阻尼系数下系统的阶跃响应
- den = [1 2 * zuni(k) *omega omega2]; % 二阶系统传递函数分母多项式系数
- sys = tf(num,den); % 二阶系统的传递函数
- y(:,k) = step(sys,t); % 计算在当前阻尼系数下二阶系统的阶跃响应值
- end
- figure(1); % 开启新的图形显示窗口
- plot(t,y(:,1:8)); % 在一幅图像上依次绘制出上述8条阶跃响应曲线
- grid; % 显示网格线
- gtext('zuni=0'); gtext('zuni=0.1'); gtext('zuni=0.2'); gtext('zuni=0.5');
- % 为曲线添加标注
- gtext('zuni=1'); gtext('zuni=2'); gtext('zuni=3'); gtext('zuni=5');
- % 为曲线添加标注
运行程序,结果如图5.49所示。
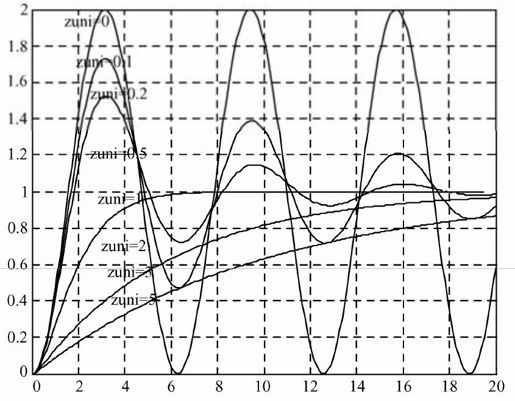
图5.49 固定自然频率,阻尼比变化时系统的阶跃响应曲线
从图5.49中不难看出,当固定自然频率后,改变二阶系统的阻尼系数ζ,在ζ<1时并不会改变阶跃响应的振荡频率;而当ζ>1时,阶跃响应曲线不再振荡,系统过阻尼。此外,当阻尼系数ζ为0时,系统的阶跃响应为等幅振荡;当0<ζ<1时,系统欠阻尼,阶跃响应曲线的振荡幅度随ζ的增大而减小,动态特性变好;当ζ>1时,系统的过渡过程时间随着ζ的增加而逐渐变长,系统响应变慢,动态特性反而下降。
利用MATLAB在一幅图像上绘制ζ=0.55,ωn从0.1变化到1时系统的阶跃响应曲线,代码如下:
- clc; % 清除屏幕显示
- clear all; % 清除工作空间中的所有变量
- t = linspace(0,20,200)'; % 设置仿真时间
- zuni = 0.55; % 设定阻尼系数
- omega = [0.1, 0.2, 0.4, 0.7, 1]; % 设置自然频率向量
- omega2 = omega.^2; % 计算自然频率的平方
- for k = 1 : 5 % 循环5次,分别计算在5种不同的自然频率下系统的阶跃响应
- num = omega2(k); % 二阶系统传递函数分子多项式系数
- den = [1 2 * zuni *omega(k) omega2(k)]; % 二阶系统传递函数分母多项式系数
- sys = tf(num,den); % 二阶系统的传递函数
- y(:,k) = step(sys,t); % 计算在当前自然频率下,二阶系统的阶跃响应值
- end
- figure(2); % 开启新的图形显示窗口
- plot(t,y(:,1:5)); % 在一幅图像上依次绘制出上述5条阶跃响应曲线
- grid; % 显示网格线
- gtext('omega=0.1'); gtext('omega=0.2'); gtext('omega=0.4'); % 为曲线添加标注
- gtext('omega=0.7'); gtext('omega=1.0'); % 为曲线添加标注
运行代码,结果如图5.50所示。
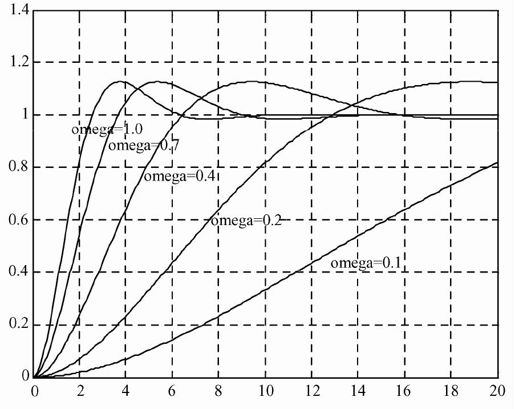
图5.50 固定阻尼系数,自然频率变化时系统的阶跃响应曲线
由图可知:当自然频率ωn从0.1变化到1时,系统的振荡频率加快,上升时间减少,过渡过程时间减少;系统响应更加迅速,动态性能变好。
自然频率ωn决定了系统阶跃响应的振荡频率。ωn越大,系统的振荡频率越高,响应速度也越快;阻尼系数ζ决定了系统的振荡幅度;当ζ<1时,系统欠阻尼,阶跃响应有超调;当ζ>1时,系统过阻尼,阶跃响应没有超调,但是响应速度大大减缓,过渡过程时间很长。经验证明,ζ=0.7时,系统的阶跃响应最好,在实际的工程应用中,通常选取ζ=0.7。
【例5-20】 已知某晶闸管-直流电机单闭环系统的结构图如图5.51所示。试分别用Simukink系统仿真和Simukink动态结构图仿真其单位阶跃响应和单位脉冲响应。
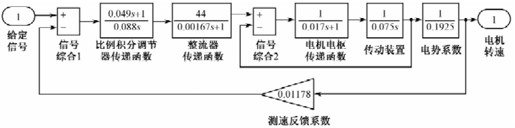
图5.51 系统结构图
解:利用Simulink的求解的基本步骤如下。
【步骤1】 在Simulink中建立该系统的动态模型,如图5.52所示,并将模型存为“Samples_5_20.mdl”。
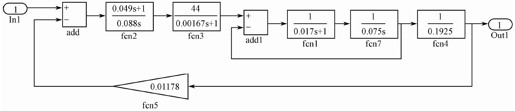
图5.52 Simulink中的系统动态模型
【步骤2】 求取系统的线性状态空间模型,并求取单位阶跃响应和脉冲响应。
在MATLAB命令窗口中运行以下命令:
- [A,B,C,D]=linmod('Samples_5_20'); %提取Simulink模型的线性状态空间模型
- sys=ss(A,B,C,D);
- figure(1); step(sys); %求取单位阶跃响应
- figure(2); impulse(sys); %求取单位脉冲响应
程序运行后,输出的阶跃曲线和脉冲曲线如图5.53和5.54所示。

图5.53 系统的单位阶跃响应曲线
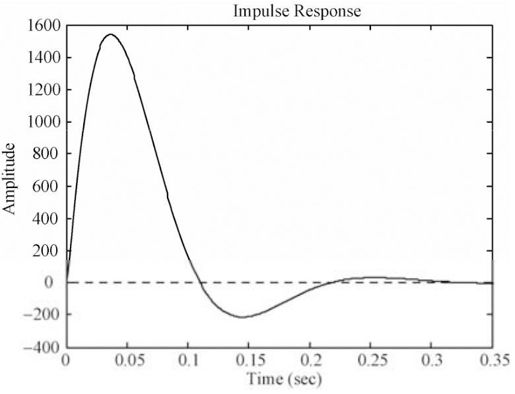
图5.54 系统脉冲响应曲线
【步骤3】 利用Simulink系统模型图仿真。
进行单位阶跃响应和单位脉冲响应仿真的系统仿真图如图5.55所示,其中,在step模块中,设置跳变时间为0,初始值为0,终止值为1,采样时间为0;impulse模块中,脉冲类型选为“Time based”,幅值设置为100,脉宽设置为1。
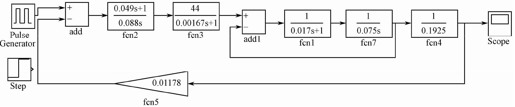
图5.55 Simulink中的系统动态仿真模型
进行阶跃响应仿真时,将step模块作为输入信号;脉冲响应仿真时,将impulse模型作为输入信号,运行后,输出的阶跃曲线和脉冲曲线如图5.56和5.57所示。
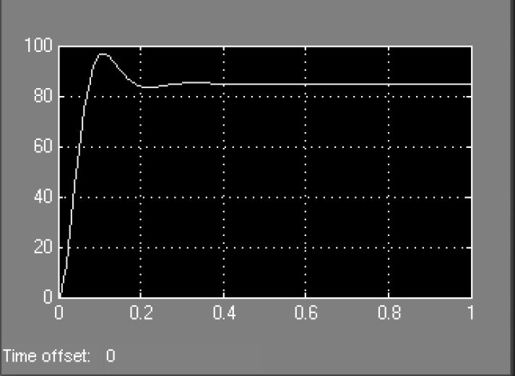
图5.56 系统单位阶跃响应
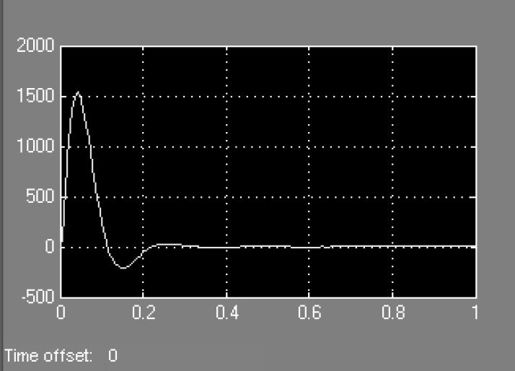
图5.57 系统脉冲响应
习 题
【5.1】 设单位负反馈控制系统的开环传递函数为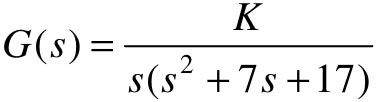 。
。
(1)试绘制K=10、100时闭环系统的阶跃响应曲线,并计算稳态误差、上升时间、超调量和过渡过程时间;
(2)绘制K=1000时闭环系统的阶跃响应曲线,与K=10、100所得结果相比较,分析增益系数与系统稳定性的关系;
(3)利用roots命令,确定使系统稳定时K的取值范围。
【5.2】 给定单位负反馈控制系统的开环传递函数G(s)分别为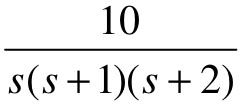 、
、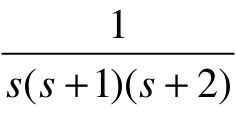 和
和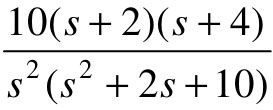 ,试判定闭环系统的稳定性,并确定当输入为阶跃信号时系统的稳态误差(如果系统稳定)。
,试判定闭环系统的稳定性,并确定当输入为阶跃信号时系统的稳态误差(如果系统稳定)。
【5.3】 已知某单位负反馈控制系统的开环传递函数为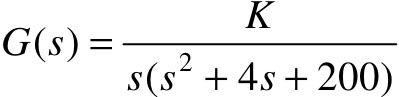 。利用MATLAB中的Simulink工具,绘制系统的结构图;并且在K取不同值时,分别绘制系统的阶跃响应曲线、冲激响应曲线以及斜坡输入响应曲线。
。利用MATLAB中的Simulink工具,绘制系统的结构图;并且在K取不同值时,分别绘制系统的阶跃响应曲线、冲激响应曲线以及斜坡输入响应曲线。
【5.4】 设系统的微分方程为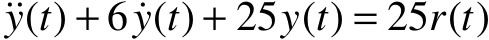 ,其中,y(t)为系统的输出变量,r(t)为系统的输入变量。
,其中,y(t)为系统的输出变量,r(t)为系统的输入变量。
(1)利用MATLAB建立上述控制系统的数学模型;
(2)绘制系统的单位阶跃响应曲线和单位冲激响应曲线。
【5.5】 设单位负反馈控制系统的开环传递函数为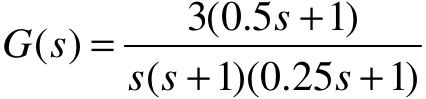 。
。
(1)利用MATLAB建立上述控制系统的数学模型;
(2)利用MATLAB绘制系统的单位阶跃响应曲线和单位冲激响应曲线;
(3)利用LTI Viewer工具绘制系统的单位阶跃响应曲线和单位冲激响应曲线。
【5.6】 已知某单位负反馈控制系统的开环传递函数为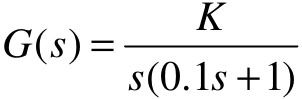 。
。
(1)假定系统的阻尼系数为0.5,计算此时的系统增益K;
(2)当K=5时,绘制闭环系统的阶跃响应曲线,并计算上升时间、稳态时间、超调量以及静态误差。
【5.7】 已知控制系统的特征方程分别为s3+3s2+2s+24=0和s5+3s4+12s3+24s2+32s+48=0,试判断系统的稳定性,如果不稳定,计算系统在右半s平面的根的数目。
【5.8】 已知单位负反馈控制系统的开环传递函数G(s)为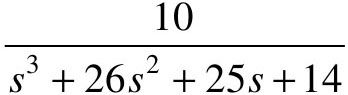 、
、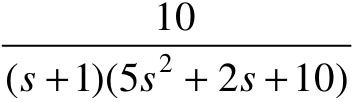 和
和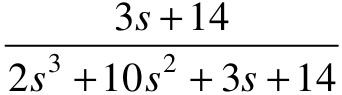 ,试分别确定其静态位置误差系数、静态速度误差系数以及静态加速度误差系数,并计算当输入信号为r(t)=2t时系统的静态误差。
,试分别确定其静态位置误差系数、静态速度误差系数以及静态加速度误差系数,并计算当输入信号为r(t)=2t时系统的静态误差。
