7.4　系统开环频率特性作图

用频率法分析控制系统时控制系统通常由若干环节组成，根据它们的基本特性，可以把系统分解成一些典型环节的串联，再按照串联的规律将这些典型环节的频率特性组合起来，即得到整个系统的开环频率特性。

7.4.1　开环对数频率特性作图

当n个环节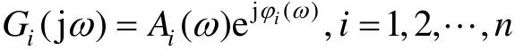串联时，串联后的系统G(jω)表示为：

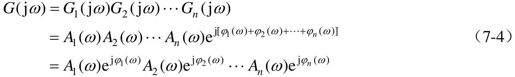
对数幅频特性L(ω)为：

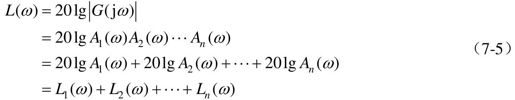
对数相频特性φ(ω)为：

可以看出，对数幅频特性采用20lgA(ω)，就可以把幅值的乘除运算简化为加减运算，从而简化曲线的绘制过程。

一般情况下，控制系统开环对数频率特性图的绘制步骤如下：

（1）将开环频率特性按典型环节分解，分解成典型环节串联的形式，并写成时间常数形式；

（2）求出各转角频率（交接频率），将其从小到大排列为ω1,ω2,ω3,…，并标注在ω轴上；

（3）绘制低频渐近线（ω1左边的部分），这是一条斜率为-20 rdB/dec（r为系统开环频率特性所含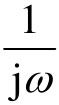因子的个数）的直线，它或者它的延长线应通过点（1, 20lgK）；

（4）各转角频率间的渐近线都是直线，但自最小的转角频率ω1起，渐近线斜率发生变化，斜率变化取决于各转角频率对应的典型环节的频率特性函数。

（5）画出各串联典型环节的相频特性，将其相加得到系统开环相频特性。

7.4.2　开环极坐标作图

设反馈控制系统的开环传递函数为G(jω)H(jω)，其中G(jω)和H(jω)分别是前向通道和反馈通道的传递函数。

系统的开环频率特性为G(jω)H(jω)，在绘制开环极坐标曲线时，可将G(jω)H(jω)写成极坐标形式：。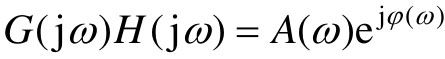

给出不同的ω，计算出相应的A(ω)和φ(ω)，即可得出极坐标图中相应的点，当ω由0→∞变化时，用光滑曲线连接就可得到系统的极坐标曲线，又称为奈氏曲线。

一般情况下，系统开环频率特性极坐标图的绘制步骤如下：

（1）将系统的开环频率特性函数G(jω)H(jω)写成。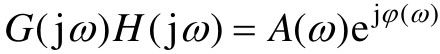

（2）确定Nyquist图的起点（ω=0+）和（ω→+∞）。起点与系统所包含的积分环节个数有关，终点的A(ω)与系统开环传递函数分母和分子多项式阶次的差有关。

（3）确定Nyquist图与坐标轴的交点。

（4）根据以上的分析并且结合开环频率特性的变化趋势绘制Nyquist图。