3.8　S函数设计与应用

3.8　S函数设计与应用
- 3.8.1　S函数设计模板
- 3.8.2　S函数设计举例

Simulink为用户提供了许多内置的基本库模块，如连续系统模块库（Continous）、离散系统模块库（Discontinous）等，通过这些模块的连接构成系统的模型。这些内置的基本库模块是有限的，在许多情况下，尤其是在特殊的应用中，需要用到一些特殊的模块，这些模块可以用基本模块构成，是由基本模块扩展而来的。

Simulink提供了一个功能强大的对模块库进行扩展的新工具S-Function，它依然是基于Simulink原来提供的内置模块，通过对那些经常使用的模块进行组合并封装而构建出可重复使用的新模块。

S-Function是系统函数（System Function）的简称，是一个动态系统的计算机语言描述。在MATLAB中，用户可以选择用M文件编写，也可以用C或mex文件编写，在这里只给大家介绍如何用M文件编写S-Function，使用C语言或mex文件编写的方法与M文件编写的方法基本类似。

S-Function提供了扩展Simulink模块库的有力工具，它采用一种特定的调用语法，实现函数和Simulink解法器之间的交互。

S-Function最广泛的用途是定制用户自己的Simulink模块。它的形式十分通用，能够支持连续系统、离散系统和混合系统。

3.8.1　S函数设计模板

对于一些算法比较复杂的模块可以使用MATLAB语言按照S-Function的格式来编写。应该注意的是，这样构造的S-Function只能用于基于Simulink的仿真，并不能将其转换成独立于MATLAB的程序。

M文件格式的S函数模板及结构

MATLAB提供了一个模板文件，方便了S-Function的编写，该模板文件位于MATLAB根目录toolbox/Simulink/blocks下，去除注释部分后的程序结构如下：

S-Function的模板
function [sys, x0, str, ts] = sfuntmpl(t, x, u, flag)
switch flag,
case 0,      % Initialization
 [sys, x0, str, ts]=mdlInitializeSizes;   %初始化子函数
case 1,      % Derivatives
sys=mdlDerivatives(t, x, u);     　　　　 %微分计算子函数
case 2,      % Update
sys=mdlUpdate(t, x, u);      　　　　　　 %状态更新子函数
case 3,      % Outputs
sys=mdlOutputs(t, x, u);     　　　　　  %结果输出子函数
case 4,      % GetTimeOfNextVarHit
sys=mdlGetTimeOfNextVarHit(t, x, u);     %计算下一个采样点的绝对时间的子函数
case 9,      % Terminate
sys=mdlTerminate(t, x, u);       　　　　%仿真结束子函数
otherwise   % Unexpected flags
error(['Unhandled flag = ', num2str(flag)]);
end

M文件S-Function可用的子函数及功能说明如下：

mdlInitializeSizes：定义S-Function模块的基本特性，包括采样时间、连续或者离散状态的初始条件和Sizes数组。
mdlDerivatives：计算连续状态变量的微分方程。
mdlUpdate：更新离散状态、采样时间和主时间步的要求。
mdlOutputs：计算S-Function的输出。
mdlGetTimeOfNextVarHit：计算下一个采样点的绝对时间，即在mdlInitializeSizes中说明了一个可变的离散采样时间。
mdlTerminate：结束仿真任务。

模板文件中S-Function的结构十分简单，它只为不同的flag值指定需调用的M文件子函数。例如，当flag=3时，即模块处于计算输出这个仿真阶段时，需调用的子函数为sys=mdloutputs(t, x, u)。

模板文件使用switch语句来完成这种指定，当然这种结构并不唯一，用户也可以使用if语句来完成同样的功能。在实际运用时，可以根据实际需要去掉某些值，因为并不是每个模块都需要经过所有的子函数调用。

模板的使用

模板文件只是Simulink为方便用户而提供的一种参考格式，并不是编写S-Function的语法要求，用户完全可以改变子函数的名称，或者直接把代码写在主函数中。但使用模板文件的好处是比较方便、条理清晰。

概括说来，建立S-Function可以分成两个分离的任务：

初始化模块特性包括输入/输出信号的宽度、离散连续状态的初始条件和采样时间。
将算法放到合适的S-Function子函数中去。

为了让Simulink识别出一个M文件S-Function，用户必须在S函数里提供有关S函数的说明信息，包括采样时间、连续或者离散状态个数等初始条件。这一部分主要是在mdlInitializeSizes子函数里完成。

Sizes数组是S-Function函数信息的载体，其内部的字段意义分别如下所述。

NumContStates：连续状态的个数（状态向量连续部分的宽度）。
NumDiscStates：离散状态的个数（状态向量离散部分的宽度）。
NumOutputs：输出变量的个数（输出向量的宽度）。
NumInputs：输入变量的个数（输入向量的宽度）。
DirFeedthrough：有无直接馈入。注意：DirFeedthrough是一个布尔变量，它的取值只有0和1两种。0表示没有直接馈入，此时用户在编写mdlOutputs子函数时就要确保子函数的代码里不出现输入变量u；1表示有直接馈入。
NumSampleTimes：采样时间的个数，也就是ts变量的行数，与用户对ts的定义有关。

如果字段代表的向量宽度为动态可变，则可以将它们赋值为-1。需要指出的是，由于S-Function会忽略端口，所以当有多个输入变量或多个输出变量时，必须用mux模块或demux模块将多个单一输入合成为一个复合输入向量或将一个复合输出向量分解为多个单一输出。

S函数模板文件的输入/输出参数

S-Function默认的4个输入参数为t、x、u和flag，它们的次序不能变动，代表的意义分别为：

t表示当前仿真时间，这个输入参数通常用于决定下一个采样时刻，或者在多采样速率系统中，用来区分不同的采样时刻点，并据此进行不同的处理。
x表示状态向量，这个参数是必须的，甚至在系统中不存在状态时也是如此，它的使用非常灵活。
u表示输入向量。
flag是一个用于控制在每一个仿真阶段调用哪一个子函数的参数，由Simulink在调用时自动取值。

S-Function默认的4个输出参数为sys、x0、str和ts，它们的次序不能变动，代表的意义分别为：

sys是一个通用的返回参数，其返回值的意义取决于flag的值。
x0是初始的状态值（没有状态时是一个空矩阵），这个返回参数只在flag值为0时才有效，其他时候都会被忽略。
str参数没有什么意义，是MathWorks公司为将来的应用保留的，M文件S-Function必须把它设为空矩阵。
ts是一个m×2矩阵，它的两列分别表示采样时间间隔和偏移。

使用模板编写S-Function，用户只需把S函数名换成期望的函数名，如果需要额外的输入参量，还需在输入参数列表的后面增加这些参数，因为前面的4个参数是Simulink调用S-Function时自动传入的。对于输出参数，最好不要修改。接下来的工作就根据所编S-Function要完成的任务，用相应的代码去替代模板里各个子函数的代码。

Simulink在每个仿真阶段都会对S-Function进行调用，在调用时，Simulink会根据所处的仿真阶段为flag传入不同的值，而且还会为sys这个返回参数指定不同的角色，即尽管是相同的sys变量，但在不同的仿真阶段其意义却不相同，这种变化由Simulink自动完成。

3.8.2　S函数设计举例

下面通过一个完整的实例讲述S函数的创建和在Simulink中应用S函数的方法。

【例3-7】　利用MATLAB中S函数模板设计一个连续系统的S-Function。给定控制系统的传递函数为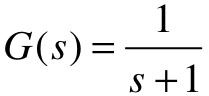 079gs-1 。试利用仿真集成环境Simulink中的S函数，绘制此控制系统的阶跃s+1响应曲线。

解：本题的基本步骤如下。

【步骤1】　获取状态空间表达式。

根据传递函数，写出该控制系统的运动方程，如下：

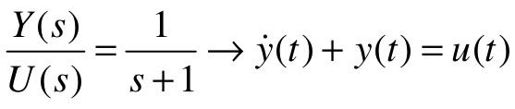
079gs-2

选取状态变量x=y，则系统的状态空间表示为：

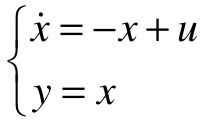
079gs-3

【步骤2】　建立S函数的M文件。

根据状态方程对MATLAB提供的S函数模板进行裁剪，得到sfunction_example.m文件。具体操作如下：复制MATLAB安装文件夹下的toolbox\simulink\blocks子目录下的sfuntmpl.m文件，并将其改名为sfunction_example.m，再根据状态方程修改程序中的代码。

具体的修改过程如下。

（1）重新命名函数。函数名需要随文件名的修改而修改，如下所示：

function [sys,x0,str,ts] = sfunction_example(t,x,u,flag,x_initial)

其中，x_initial是状态变量x的初始值，它需要在Simulink对系统进行仿真前由用户手工赋值。

主函数部分的代码如下：

switch flag,
  case 0,     % Initialization，初始化%
    [sys,x0,str,ts]=mdlInitializeSizes(x_initial);
 　case 1,    % Derivatives，计算模块导数%
    sys=mdlDerivatives(t,x,u);
 　case 2,    % Update，更新模块离散状态%
    ys=mdlUpdate(t,x,u);
 　case 3,    % Outputs，计算模块输出%
    sys=mdlOutputs(t,x,u);
 　case 4,    % GetTimeOfNextVarHit，计算下一个采样时间点%
    sys=mdlGetTimeOfNextVarHit(t,x,u);
 　case 9,    % Terminate，仿真结束%
    sys=mdlTerminate(t,x,u);
   otherwise  % Unexpected flags，出错标记 %
    error(['Unhandled flag = ',num2str(flag)]);
end

（2）修改“初始化”子函数部分的代码。修改后的代码如下：

% 由于状态变量x的初始状态是用户事先设定的，所以输入参数列表中需加入x_initial
  function [sys,x0,str,ts]=mdlInitializeSizes(x_initial)
  sizes = simsizes;           % 用于设置模块参数的结构体用simsizes来生成
  sizes.NumContStates  = 1;   % 系统中的连续状态变量个数为1
  sizes.NumDiscStates  = 0;   % 系统中的离散状态变量个数为0
  sizes.NumOutputs     = 1;   % 系统的输出个数为1
  sizes.NumInputs      = 1;   % 系统的输入个数为1
  sizes.DirFeedthrough = 0;   % 输入和输出间不存在直接比例关系
  sizes.NumSampleTimes = 1;   % 只有1个采样时间
  sys = simsizes(sizes);      % 设置完后赋给sys输出
  x0  = x_initial;            % 设定状态变量的初始值
  str = [];                   % 固定格式
  ts  = [0 0];                % 该取值对应纯连续系统

（3）修改“计算模块导数”子函数部分的代码。修改后的代码如下：

function sys=mdlDerivatives(t,x,u)
  dx = -x + u                % 对应于系统的状态空间方程
  sys = dx;                  % 把计算得出的导数向量赋值给sys变量

（4）修改“更新模块离散状态”子函数部分的代码。修改后的代码如下：

function sys=mdlUpdate(t,x,u)
sys = [];

因为本题讨论的是连续时间系统，所以这部分代码无须修改。

（5）修改“计算模块输出”子函数部分代码。修改后的代码如下：

function sys=mdlOutputs(t,x,u)
sys = x;

因为题目中给定的系统阶次为1，输出方程为y=x，所以只需要将计算得到的状态值x赋值给sys即可。

（6）修改“计算下一个采样时间点”子函数部分的代码。修改后的代码如下：

function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1;
sys = t + sampleTime;

这部分代码表示此时要计算下一次采样的时间，只在离散采样系统中有用（即上文的mdlInitializeSizes中提到的ts设置ts(1)不为0）。

本例中，这部分代码无须修改，直接采用默认设置。

（7）修改“仿真结束”子函数部分的代码。修改后的代码如下：

function sys=mdlTerminate(t,x,u)
sys = [];

这部分代码表示此时系统要结束，一般来说在mdlTerminate函数中写上sys=[]就可，也无须修改，直接采用默认设置。如果需要在结束时进行一些设置，就在此函数中编写代码。

此外，出错标记采用默认设置即可，无须改动。

至此，S函数的代码编写工作已经完成。

【步骤3】　将sfunction_example创建成S-Function模块。

打开Simulink，在Simulink中新建一个空白的模型窗口，拖动“User-Defined Functions”库中的S-Function模块到其中，并相应放置输入的阶跃信号发生器和检测输出波形的示波器，如图3.37所示。

081-3

图3.37　S函数应用举例

【步骤4】　给状态变量赋初始值。

在进行真正的仿真之前，还需要在MATLAB工作空间为状态变量x的初始值x_initial进行赋值。在MATLAB工作空间中输入如下命令：

clear;
x_initial = 0;

参数设定之后，启动Simulink仿真，仿真结果如图3.38所示。

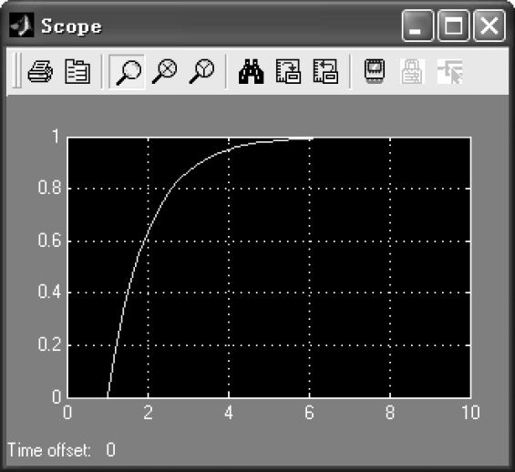
082-01

图3.38　利用S函数仿真的结果

为了验证上述结果，可以在Simulink中搭建如图3.39所示的系统。

082-1

图3.39　直接用传递函数模型验证S函数的正确性

启动仿真，输出的结果和图3.38完全相同。两次仿真的结果完全相同证明了上述S函数的代码正确。

从前面的分析可知，对于比较复杂的系统，可以通过编写S函数对系统进行建模，这无疑大大扩展了MATLAB对系统仿真的能力。

3.8 S函数设计与应用