2.7　复数和复变函数运算

复数及在其基础上发展起来的复变函数这一重要的数学分支，解决了许多实变函数无法解决的问题，有着广泛的工程应用。

复变函数是控制工程的数学基础，常用来描述控制系统模型的传递函数就属于复变函数。MATLAB支持在运算和函数中使用复数或复数矩阵，还支持复变函数运算。下面讲述MATLAB中的基本复数运算，以及留数运算、泰勒级数、傅里叶变换、拉普拉斯变换和Z变换。

2.7.1　复数运算基础

1. 复数的一般表示

MATLAB是以i或j字元来代表虚部复数运算的。

一个复数可表示为：x=a+bi，其中a称为实部，b称为虚部。

也可写成复指数形式：x=reiθ。其中r称为复数的模，又记为|x|；θ称为复数的幅角，又记为arctan(x)，且满足如下关系：

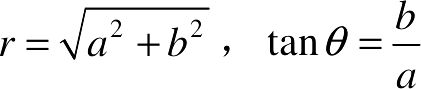
具体采用哪种表示方法取决于实际问题。一般而言，第一种问题适合处理复数的代数运算，第二种方法适合处理复数旋转等涉及幅角改变的问题。

一个复数也可以看做关于实部和虚部的符号函数。因此，既可以直接构造复数，也可以用符号函数构造复数。下面分别介绍这两种构造方法。

（1）用直接法构造两种形式的复数。直接法就是利用符号i或j来表示复数单位，将复数看做完整的一个表达式输入。其具体形式也有两种，可以用实部和虚部形式表示，也可以用复指数形式表示。

（2）用符号函数法构造两种形式的复数。所谓符号函数法就是将复数看成函数形式，其实部和虚部看做自变量，用syms来构造，用subs对符号函数中自变量进行赋值。

【例2-9】　构造复数实例。试分别使用上述两种方法在MATLAB中构造复数x=-1+i。

解：在MATLAB命令窗口中输入：

x1=-1+i                          %直接法构造，实部虚部形式
x2=sqrt(2)*exp(i*(3*pi/4))       %直接法构造，复指数形式
%符号函数法构造,实部虚部形式
syms a b real;                   %声明a,b为实数型
x3=a+b*i                         %实部虚部形式复数的符号表达
subs(x3,{a,b},{-1,1})            %代入具体值
%符号函数法构造,复指数形式
syms r ct real;                  %声明r,ct为实数型
x4=r*exp(ct*i);                  %复指数形式复数的符号表达
subs(x4,{r,ct},{sqrt(2),3*pi/4}) %代入具体值

输出结果为：

x1 = -1.0000 + 1.0000i
x2 = -1.0000 + 1.0000i
x3 = -1.0000 + 1.0000i
x4 = -1.0000 + 1.0000i

1. 复数矩阵的表示

MATLAB中矩阵运算贯穿始终，复数矩阵也是其中的一个重要方面。由于复数矩阵的每个元素都是复数，所以对应的复数创建矩阵也有两种，即直接创建和利用符号函数创建。

复数矩阵的直接创建有两种方法：一种是由复数元素构造复数矩阵；另一种是利用两个矩阵分别做实部和虚部构造新的复数矩阵。下面举例说明复数矩阵的直接创建，另一种方法很容易实现，在此不再赘述。

（1）由复数元素构造复数矩阵。复数矩阵的每个元素都是复数，将复数作为矩阵元素并按照矩阵格式进行填充就得到了复数矩阵。

（2）由实矩阵创造复数矩阵。由两个分别作为实部和虚部的同维矩阵构造复数矩阵。

【例2-10】　由复数元素构造复数矩阵实例。构造复数矩阵。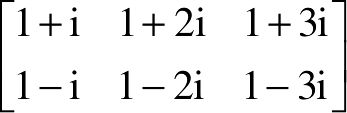

解：可直接输入各元素来构造矩阵，此处通过其复指数形式构造。

在MATLAB命令窗口中输入：

%直接输入各元素来构造
A1=[sqrt(2)*exp((pi/4)*i) 1+2i 1+3i;sqrt(2)*exp((-pi/4)*i) 1-2i 1-3i] %
%由实矩阵构
A2re=[1 1 1;1 1 1]; A2im=[1 2 3;-1 -2 -3]; A2=A2re+A2im*i

输出结果A1和A2均为：

1.0000 + 1.0000i   1.0000 + 2.0000i   1.0000 + 3.0000i
1.0000 - 1.0000i   1.0000 - 2.0000i   1.0000 - 3.0000i

1. 复数绘图

对于复数函数的绘图主要有两种形式：一种是直角坐标图，即分别以复数的实部和虚部为坐标画出复数的表示图；另一种为极坐标图，即分别以复数的模和幅角为坐标画图。

MATLAB提供了绘制极坐标图的函数polar，它还可绘制出极坐标栅格线，其常用的调用格式为：

polar(theta,rho)

其中，theta为极坐标极角，rho为极坐标矢径。

【例2-11】　复数函数绘图实例。画出函数y=t+itsin(t)在两种坐标下的表示图，如图2.12所示。

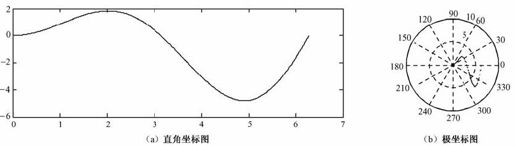
图2.12　极坐标下复数的表示

解：直角坐标图——以实部为横坐标，以虚部为纵坐标；极坐标图——以模为极半径，以幅角为极角，在MATLAB命令窗口中输入：

t=0:0.01:2*pi; y=t+i*t.*sin(t);  %直角坐标表示
r=abs(y);bdelta=angle(y);        %极坐标表示
subplot(2,1,1)
plot(y)                          %绘制直角坐标图
title('直角坐标图') ; subplot(2,1,2)
polar(delta,r)                   %绘制极坐标图
title('极坐标图')

1. 复数的结构操作函数

对于一个形如x=a+bi的复数，通常希望能够了解它自身的结构性质，包括实部、虚部、模和幅角等。MATLAB提供了方便的操作函数。下面利用实例来说明各个函数的调用方法。

表2.13　复数的结构操作函数

在MATLAB中，复数的基本运算和实数相同，都是使用相同的函数。比如复数或复数矩阵x除以y，运算命令也是x/y，与实数运算一样。因此，复数基本运算的内容此处不再赘述。

1. 留数及其基本运算

留数的定义：设a是f(z)的孤立奇点，C是a的充分小的邻域内一条把a点包含在其内部的闭路，积分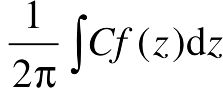称为f(z)在a点的留数或残数，记做Res[f(z),a]。

留数定理：如果函数f(z)在闭路C上解析，在C的内部除去n个孤立奇点a1,a2,…,an外也解析，则闭路上的积分满足

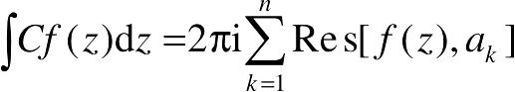
如果能够求得函数f(z)在各极点的留数的显式表达，则该闭路积分很容易获得。

由罗朗展开，若a是f(z)的m重极点，则函数在该点的留数可以表示为：

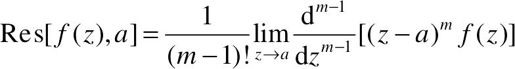
至此，通过留数定理可以把闭路积分转化为简单的代数计算。

由于在工程中遇到的f(z)多数情况下为有理分式，所以可表示为如下形式：

函数residue可以求得该有理式的留数，residue的返回参数有3个，分别对应留数向量、极点向量和高阶项。

调用格式：

[r, p, k] = residue([an an-1 … a0], [bn bn-1 … b0])

如果仅对留数感兴趣，后两个参数可省略。

2.7.2　拉普拉斯变换及逆变换

在MATLAB中，可以采用符号运算工具箱进行拉氏变换（拉普拉斯变换的简称）和拉氏反变换，采用的函数是laplace和ilaplace，使用前，用syms函数设置有关的符号变量。在MATLAB的符号工具箱中，有拉氏变换和拉氏反变换的运算函数，下面进行简单介绍。

符号变量设置函数syms的格式为：syms arg1 arg2…，用于设置符号运算中的变量arg1、arg2等。也可以用arg1=sym('arg1'); arg2=sym('arg2');…来进行符号变量设置。

当需要说明变量的数据类型时，可采用以下格式：syms arg1 arg2…datatype。其中datatype可以是实型（real）、整型（positive）、非实型（unreal）等。

laplace变换函数的格式为：

L=laplace(F)

其中，F是时域函数表达式，约定的自变量是t，得到的拉氏变换函数是L(s)。

ilaplace拉氏反变换函数的常用格式为：

F=ilaplace(L)

它将L拉氏函数变换为时域函数F。

【例2-12】　求函数f1(t)=eat（a为实数）、f2(t)=t-sint的拉氏变换。

解：MATLAB程序代码如下。

syms t s a                        %创建符号变量
f1=exp(a*t); f2=t-sin(t)          %定义函数
L1=laplace(f1); L2=laplace(f2)    %进行拉氏变换

程序运行后，输出的结果为：

L1 =1/(s-a)
L2 =1/s^2-1/(s^2+1)

由运行结果可知，，。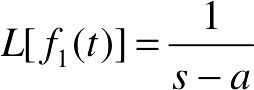

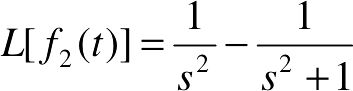【例2-13】　求函数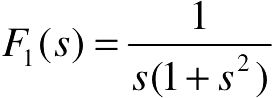、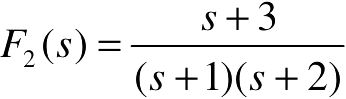的拉氏反变换。

解：MATLAB程序代码如下。

syms t s                                       %创建符号变量
F1=1/( s*(1+s^2) ); F2=(s+3)/((s+1)*(s+2) )    %定义函数
f1=ilaplace(F1); f2=ilaplace(F2)               %进行拉氏反变换

程序运行后，输出的结果为：

f1=1-cos(t)
f2=2*exp(-t)-exp(-2*t)

由运行结果可知，L-1[F1(S)]=1-cos(t), L-1[F2(S)]=2e-t-e-2t，t≥0。

2.7.3　Z变换及其反变换

MATLAB提供了符号运算工具箱（Symbolic Math Toolbox），可方便地进行Z变换和Z反变换，进行Z变换的函数是ztrans，进行Z反变换的函数是iztrans。

1. ztrans

函数常用的调用格式如下。

F=ztrans(f)：函数返回独立变量n关于符号向量f的Z变换函数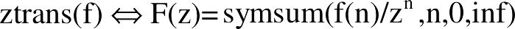：，这是默认的调用格式。

F=ztrans(f, w)：函数返回独立变量n关于符号向量f的Z变换函数，只是用w代替了默认的z：。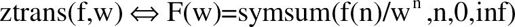

F=ztrans(f, k, w)：函数返回独立变量n关于符号向量k的Z变换函数：。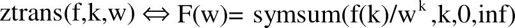

1. iztrans

函数常用的调用格式如下。

f=iztrans(F)：函数返回独立变量z关于符号向量F的Z反变换函数，这是默认的调用格式。

f=iztrans(F, k)：函数返回独立变量k关于符号向量F的Z反变换函数，只是用k代替了默认的z。

f=iztrans(F, w, k)：函数返回独立变量w关于符号向量F的Z反变换函数。

【例2-14】　试求函数f1(t)=t、f2(t)=e-at、f3(t)=sin(at)的Z变换。

解：使用MATLAB提供的符号工具箱函数进行计算，程序代码如下。

syms n a w k z T                                %创建符号变量，T为采样周期
x1=ztrans(n*T); x1=simplify(x1)                 %进行Z变换并化简结果
x2=ztrans(exp(-a*n*T)); x2=simplify(x2)         %进行Z变换并化简结果
x3=ztrans(sin(w*a*T), w, z) ;  x3=simplify(x3)  %进行Z变换并化简结果

运行结果如下：

x1 =T*z/(z-1)^2
x2 =z*exp(a*T)/(z*exp(a*T)-1)
x3 =z*sin(a*T)/(z^2-2*z*cos(a*T)+1)

可见，变换结果为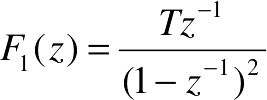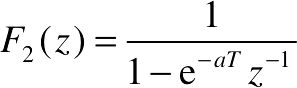：、和。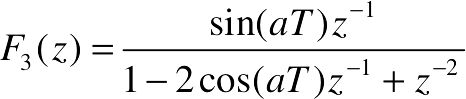

【例2-15】　试求函数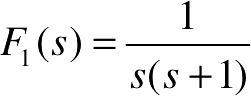、、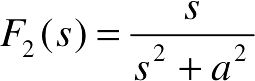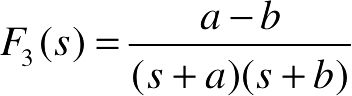的Z变换。

解：使用MATLAB提供的符号工具箱函数进行计算，由于只有时域的Z变换，因此对于拉氏域首先需要进行拉氏反变换，程序代码如下。

syms s n t1 t2 t3 a b k z T                            %创建符号变量，T为采样周期
x1= ilaplace(1/s/(s+1), t1);  x1=simplify(x1)          %进行拉氏反变换并化简结果
x2= ilaplace( s/(s^2+a^2), t2) ; x2=simplify(x2)       %进行拉氏反变换并化简结果
x3= ilaplace( (a-b)/(s+a)/(s+b), t3) ; x3=simplify(x3) %进行拉氏反变换并化简结果

运行结果如下：

x1 =1-exp(-t1)
x2 =cos(csgn(a)*a*t2)           % csgn(a)求a的符号
x3 =-exp(-a*t3)+exp(-b*t3)

对拉氏反变换结果进行Z变换，注意把时间参数t1, t2, t3都替换成n*T，在命令窗口中输入：

>>x1=ztrans(1-exp(-n*T));  x1=simplify(x1)
>> x2=ztrans(cos((a^2)^(1/2)*n*T));  x2=simplify(x2)
>>  x3=ztrans(-exp(-a*n*T)+exp(-b*n*T));  x3=simplify(x3)

运行结果如下：

x1 =z*(-1+exp(T))/(z-1)/(z*exp(T)-1)
x2 =(z-cos(signum(a)*a*T))*z/(z^2-2*z*cos(signum(a)*a*T)+1) % signum(a)求a的符号
x3 = -z*(-exp(a*T)+exp(b*T))/(z*exp(a*T)-1)/(z*exp(b*T)-1)

可见，变换结果为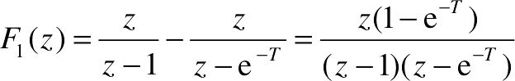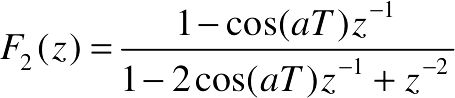：、和。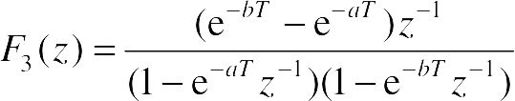

【例2-16】　试求函数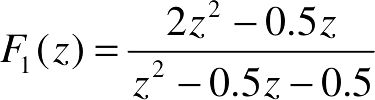和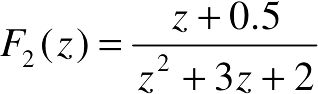的Z反变换。

解：使用MATLAB提供的符号工具箱函数进行计算，程序代码如下。

syms z a k T            %创建符号变量，T为采样周期
x1=iztrans( (2*z^2-0.5*z)/(z^2-0.5*z-0.5)); x1=simplify(x1) %进行Z反变换并化简结果
x2=iztrans( (z+0.5)/(z^2+3*z+2) ); x2=simplify(x3)  %进行Z反变换并化简结果

运行程序，输出拉氏反变换结果如下：

x1 =(-1)^n*2^(-n)+1
x2 =1/2*(-1)^n+3/4*(-1)^(1+n)*2^n

可见，变换结果为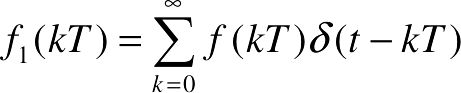和。