4.7　非线性数学模型的线性化

系统如果不能应用叠加原理，则系统是非线性的。在建立控制系统的微分方程时，常常遇到非线性方程。由于解非线性微分方程比较困难，因而提出了非线性特性的线性化问题。如果我们能够做某种近似，或者缩小一些研究问题的范围，那么大部分非线性特性都可以近似地作为线性特性来处理，这会给控制系统研究工作带来诸多方便。虽然这种方法是近似的，但在一定范围内能够反映系统的特性，在工程实践中有很大的实际意义。

在控制工程中，如果系统的运行是围绕平衡点进行的，并且系统中的信号是围绕平衡点变化的小信号，那么就可以用线性系统去近似非线性系统。这种线性系统在有限的工作范围内等效于原来的非线性系统。在控制工程中，这种线性化模型（线性定常模型）是很重要的。

线性化过程用数学方法来处理就是将一个非线性函数y=f(x)，在其工作点(x0,y0)处展开成泰勒级数，然后忽略其二次以上的高阶项得到线性化方程，并以此代替原来的非线性函数。因为忽略了泰勒级数展开中的高阶项，所以这些被忽略的项必须很小，即变量只能对工作状态有微小的偏离。

对于具有一个自变量的非线性函数，设其输入量为x(t)，输出量为y(t)，系统正常工作点为y0=f(x0)，那么在f(x0)附近展开成泰勒级数为：

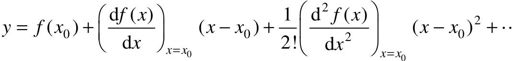
式中，导数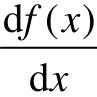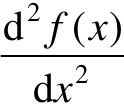，，…均是在x=x0点上计算得到的。如果变量的变化x-x0很小，则可以忽略二次以上的项，可写成：

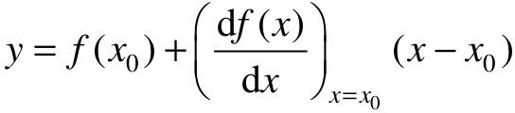
或

式中，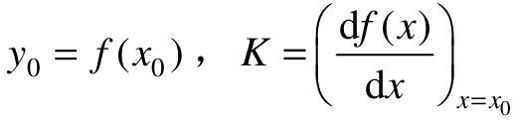

式（4-1）表明y-y0与x-x0成正比，式（4-1）就是方程y0=f(x0)在工作点(x0,y0)附近的线性化模型。

对于多输入量函数的线性化，下面以两个输入变量的函数y=f(x1,x2)在工作点x1=x10，x2=x20处的线性化为例进行介绍。

方程y=f(x1,x2)在工作点附近展开成泰勒级数如下：

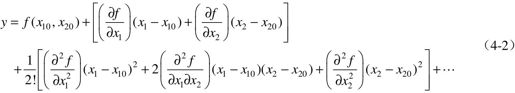
式中，偏导数都在x1=x10，x2=x20上计算得到，在工作点附近，高阶项可以忽略不计，于是式（4-2）可以写成如下形式：

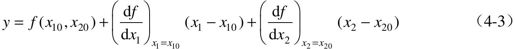
或

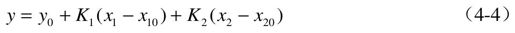
式中，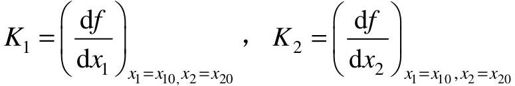

上述线性化方法只有在工作状态附近才是正确的。当工作状态的变化范围很大时，线性化方程就不合适了，这时必须使用非线性方程。应当特别注意，在分析和设计中采用的具体数学模型只是在一定的工作条件下才能精确地表示实际系统的动态特性，在其他工作条件下它可能是不精确的。