6.6　综合实例及MATLAB/Simulink应用

6.6　综合实例及MATLAB/Simulink应用

下面通过一个综合实例，讲述MATLAB/Simulink在本章中的应用。

【例6-10】　已知单位负反馈控制系统的开环传递函数为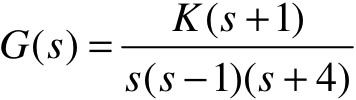 170-2

（1）画出这个系统的根轨迹；

（2）确定使闭环系统稳定的增益值K；

（3）分析系统的阶跃响应性能；

（4）利用rltool对系统的性能进行分析。

解：利用MATLAB求解的基本步骤如下。

【步骤1】　建立系统的数学模型。

利用MATLAB，对该控制系统建模，代码如下。

clc;                     % 清除命令窗口的显示
clear;                   % 清除工作空间的所有变量
num = [1 1];             % 开环传递函数分子多项式系数
den = conv([1 0],conv([1 -1],[1 4]));   % 开环传递函数分母多项式系数
sys = tf(num,den)        % 控制系统的开环传递函数模型

程序运行结果如下：

Transfer function:
    s + 1
-------------------
s^3 + 3 s^2 - 4 s

结果输出的是用来绘制根轨迹的那部分传递函数。

【步骤2】　绘制根轨迹。

根据已经建立的数学模型，绘制系统的根轨迹曲线，代码如下：

rlocus(sys);           % 绘制系统的根轨迹曲线
grid on;               % 显示网格线
title('根轨迹图');     % 给曲线添加标题

得到的系统根轨迹如图6.20所示。

171-1

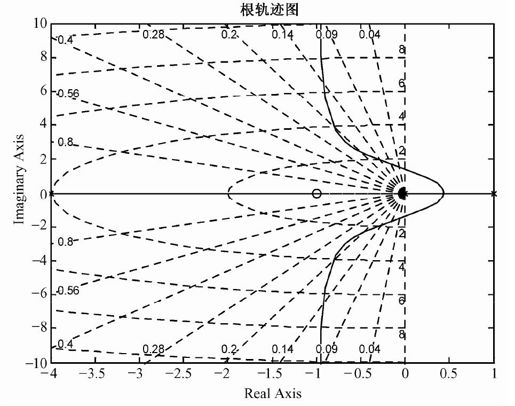
图6.20　系统根轨迹图

图6.20中，“×”表示闭环系统的极点，“○”表示闭环系统的零点。用鼠标单击图中的曲线，可以得到对应的系统增益、极点、频率等参数。如图6.21所示。

171-2

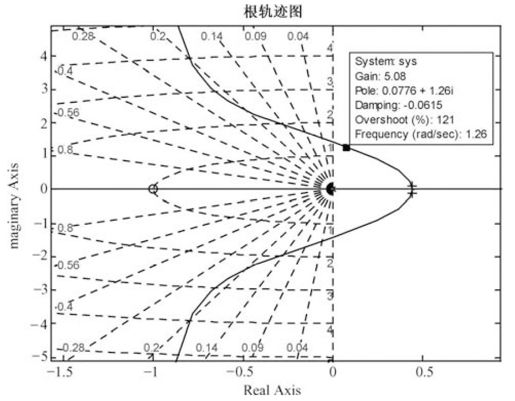
图6.21　从根轨迹图中读取系统参数

得到根轨迹图后，可以利用“rlocfind”命令计算用户选定点处的增益和其他闭环极点。根据题目要求，需要求得根轨迹穿越虚轴时的系统增益，以此确定稳定的增益范围。代码如下：

[k,poles] = rlocfind(sys)     % 计算用户所选定的点处的增益和其他闭环极点

运行程序，单击根轨迹与虚轴的交点，直接在图中进行选取，精度往往较差。可以将曲线局部放大，结果如图6.22所示。

172-1

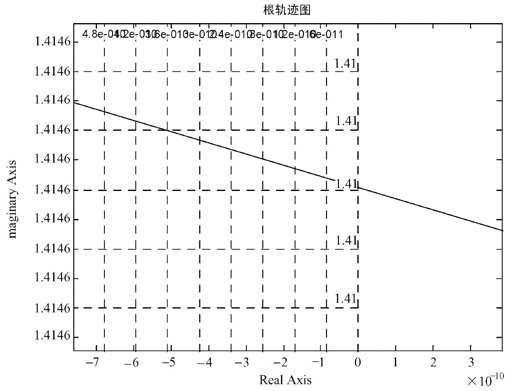
图6.22　选取根轨迹与虚轴的交点

同时得到：

k = 6.0018
poles = -2.9997
    -0.0002 + 1.4145i
    -0.0002 - 1.4145i

可见，当增益K>6时，闭环系统的极点都位于虚轴的左部，处于稳定态。

【步骤3】　使用rltool进行分析。

使用根轨迹分析与设计的工具rltool，执行命令“rltool(sys)”就可以得到控制系统sys的根轨迹分析图形界面。如图6.23所示。

172-2

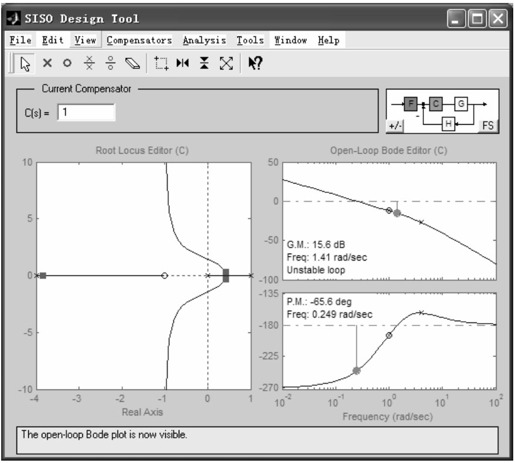
图6.23　控制系统根轨迹分析与设计器

在Current Compensator编辑器中输入不同的值，Root Locus Editor中会立刻显示出对应的极点。设定系统增益为6，如图6.24所示。

173-1

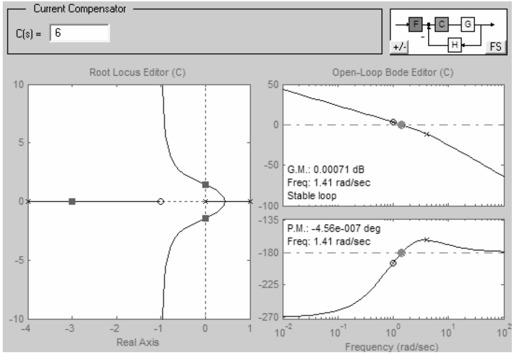
图6.24　设定系统增益为6时的根轨迹和Bode图

从图6.24中不难看出，K=6恰好是系统的临界增益，这与rlocfind命令得出的结果是相符的。利用rltool还可以在根轨迹图中增加、删除系统的零极点，是一个非常方便的工具。

至此，已经得出使系统稳定的增益范围。取K=6（临界增益），容易分析出系统此时的阶跃响应应当是等幅振荡。

此外，还可以利用rltool工具分析系统的阶跃响应。设定系统增益为20，在rltool界面下选择Analysis菜单，单击Response to Step Command，得到如图6.25所示的结果。

173-2

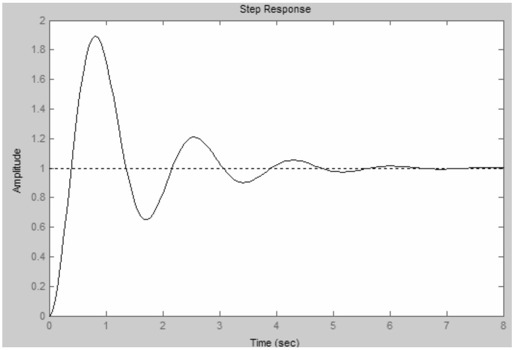
图6.25　K=20时系统的阶跃响应

可见，系统稳定，并且稳态误差为0。此时，系统的穿越频率为1.41，相角稳定裕度为17，剪切频率为3.68。

当然，还可以利用step命令直接得到阶跃响应曲线。执行“step(feedback(20*sys, 1))”即可，运行结果完全相同。

习　题

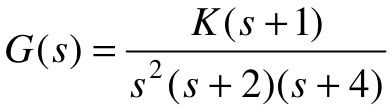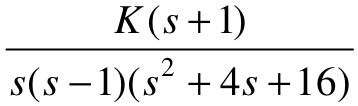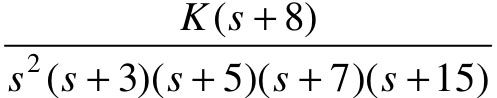【6.1】　已知单位负反馈控制系统的前向传递函数分别为 174-1 、 174-2 和 174-3 ，试利用MATLAB分别绘制各系统的根轨迹图。

【6.2】　某单位负反馈控制系统的开环传递函数为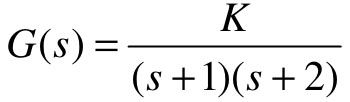 174-4 。

（1）利用MATLAB中的rltool工具，绘制系统的根轨迹图，并确定使闭环系统稳定的K的取值范围；

（2）在rltool中，尝试添加新的极点（-3,0），观察根轨迹的变化，并且确定使闭环系统稳定的K的取值范围，继续尝试添加其他的零点、极点，分析根轨迹的变化；

（3）在Simulink中对上述系统建模，给出K取不同值时系统在阶跃信号下的响应曲线，验证（2）中的结论。

【6.3】　已知单位负反馈控制系统的开环传递函数为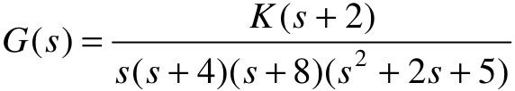 174-5 。

（1）绘制系统的根轨迹曲线；

（2）求系统临界稳定时增益系数K的取值。

【6.4】　已知单位负反馈控制系统的开环传递函数为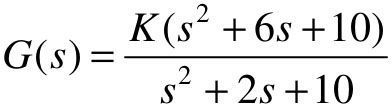 174-6 。

（1）绘制系统的根轨迹曲线，并确定使闭环系统稳定的K的取值范围；

（2）上述控制系统的根轨迹有何特点？

【6.5】　设单位负反馈控制系统的结构如图6.A所示。

174-9

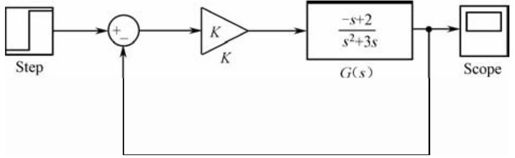
图6.A　习题

（1）在MATLAB中建立上述控制系统的数学模型；

（2）绘制系统的根轨迹曲线；

（3）判断点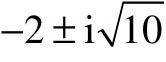 174-7 是否在根轨迹曲线上；

（4）确定使闭环系统稳定的K的取值范围。

【6.6】　已知单位负反馈控制系统的结构如图6.B所示。

175-1

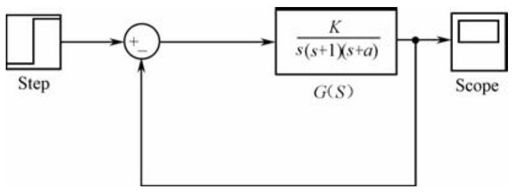
图6.B　习题

在MATLAB中编程实现如下功能：当参数a从0变化到无穷大时，绘制出系统的根轨迹族（提示：实际编程时，可以给参数a赋以几个离散的值。只需反应出根轨迹的变化趋势即可）。

【6.7】　某种机械手型机器人的传递函数为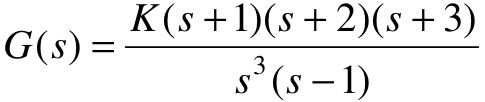 175-2 。

（1）在MATLAB中建立上述控制系统的数学模型；

（2）绘制机械手控制系统的根轨迹曲线；

（3）确定使闭环系统稳定时K的取值；

（4）在第三问得出的K的范围中，选取一组不同的K值，分别绘制闭环系统的阶跃响应曲线，并且比较曲线之间的异同。

6.6 综合实例及MATLAB/Simulink应用