5.2　时域响应分析

时域响应指的是系统在外部输入（设定值输入或扰动输入）作用下的输出过程。

5.2.1　典型输入

为了研究自动控制系统的暂态特性和稳态特性，需要知道输入量的变化规律，但通常是不能准确知道输入量的变化的。不同的输入形式其响应是不同的，为了便于比较，常用一些规定的输入形式作为系统输入来检查系统的性能，这些输入就称为典型输入。自动控制系统通常使用的典型输入信号有脉冲输入、阶跃输入、斜坡输入、加速度输入和正弦输入。利用这些典型输入信号易于对系统进行试验和数学分析。

1. 单位脉冲输入

单位脉冲输入定义为：

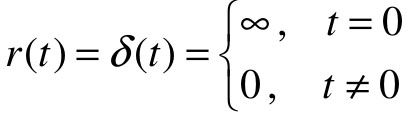
其中，

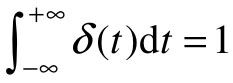
其拉氏变换为：

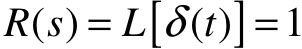
单位脉冲函数的幅值为无穷大，持续时间为零，纯属数学上的假设，但在系统分析中是很有用的。实际中，常用系统受到单位脉冲输入作用后的输出来衡量系统的暂态响应特性。

单位脉冲响应的拉氏变换就是系统的传递函数。如果在系统输入端加一单位脉冲函数，由输出响应即可求得系统的传递函数。

在分析闭环系统时，单位脉冲输入具有重要意义。根据系统的脉冲响应可以求出系统的传递函数，并且可以求出任意输入信号下的系统响应。

1. 单位阶跃输入

单位阶跃输入的定义及拉氏变换为：

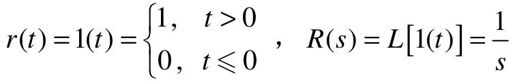
在t=0处的阶跃信号相当于一个不变的信号突然加到系统上。对于恒值系统，相当于给定值突然发生变化；对于随动系统，相当于加一个突变的给定位置信号。

1. 单位斜坡输入

单位斜坡输入的定义及拉氏变换为：

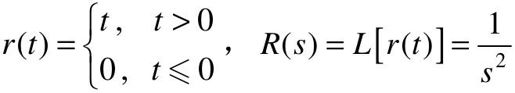
单位斜坡输入对于随动系统，相当于加一个恒速变化的位置信号。

1. 单位加速度输入

单位加速度输入的定义及拉氏变换为：

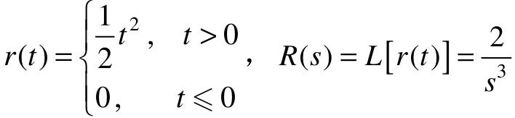
单位加速度输入对于随动系统，相当于加一个恒加速度变化的位置信号。

1. 单位正弦输入

单位正弦输入的定义及拉氏变换为：

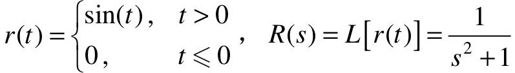
利用单位正弦输入可以求得系统对不同频率的稳态响应，由此可以间接判断系统性能。

典型输入的选用应视不同系统要求而定。例如，对于恒值控制系统通常用阶跃输入；对于随动系统通常用斜坡输入和加速度输入；对于扰动与响应系统通常用阶跃输入和脉冲输入。

5.2.2　线性系统时域响应一般求法

设已知系统的传递函数为：

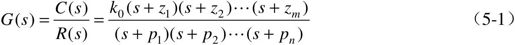
且输入为：

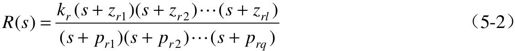
式中，-zr1, -zr2, …, -zrl及-pr1, -pr2, …, -prq分别是输入函数r(t)拉氏变换式R(s)的零点和极点，通常简称为输入零点和极点。

那么，

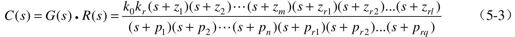
5.2.2.1　G(s)无重极点的情况

若式（5-3）中无重极点，则C(s)可分解为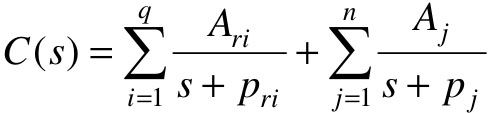：，那么，

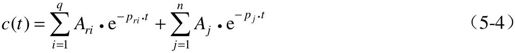
式中，，。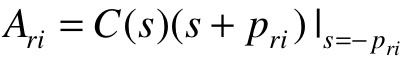

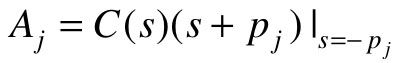通常把c(t)表达式中线性独立的分量和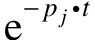称为模态，它取决于传递函数的极点和输入极点。模态的特征是发散还是收敛，是单调变化还是振荡，决定了响应的基本特征。

Ari和Aj称为C(s)的留数，它由C(s)的极点和零点共同决定。留数的大小和模态共同决定了响应。

由此可知，系统时域响应的特征是由闭环极点决定的。零点可以影响c(t)的具体变化形状。另一方面，通常把式（5-4）中的第一项称为响应的稳态分量，它和输入极点有关；第二项称为响应的动态分量，它和系统传递函数的极点有关。当然，系统本身的动态性能是由其动态分量决定的。

5.2.2.2　G(s)有重极点的情况

C(s)有重极点时，方法有所不同，下面进行简要说明。

设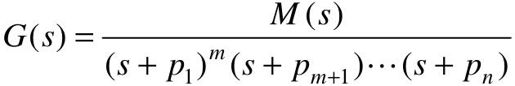，其中，-p1是m重极点，那么，

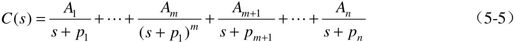
式中，

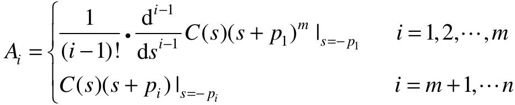
而

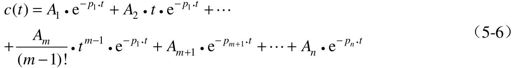
5.2.3　时域响应性能指标

5.2.3.1　阶跃响应性能指标

当已知时域响应c(t)时，按c(t)的形状就大致可判断出其动力学性能的优劣。一般来说，对系统输出响应的要求可以用两个基本要求和三个衡量标准来概括。

两个基本要求是：对设定值输入的跟随和对扰动输入的抑制。

三个衡量标准是：跟随和抑制过程的稳定性、快速性和准确性。

下面对设定值为阶跃信号的响应加以说明，通常将之称为阶跃响应。阶跃响应的一般情况如图5.1所示。

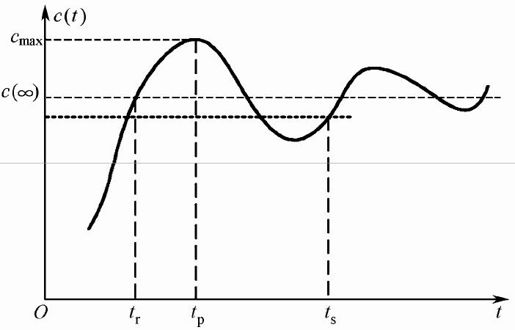
图5.1　阶跃响应瞬态指标图

图5.1中，tr称为上升时间，它表示c(t)第一次达到稳态值c(∞)的时间。对于单调无超调过程显然该定义不适用，一般可定义为c(t)从0.1c(∞)上升到0.9c(∞)所需的时间。

（1）tp称为峰值时间，它表示c(t)达到最大值cmax的时间。

（2）σp%称为超调量，且

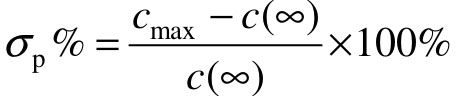
（3）ts称为调节时间，且

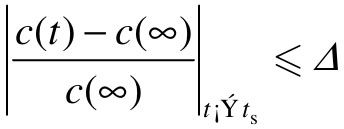
式中，Δ称为允许误差，一般取Δ=0.05或Δ=0.02。

上述指数显然从不同的侧面反映了系统的性能，其中tr反映了快速性，σp%反映了稳定性，而ts是稳定性和快速性的一种综合。

5.2.3.2　误差积分指标

上述指标从不同侧面衡量了系统的性能，但在系统分析和最优设计时还需用到一种误差积分指标。

定义误差函数e(t)=c(∞)-c(t)，如图5.2中的阴影部分所示。显然，阴影部分的面积越小则跟随性能越好。

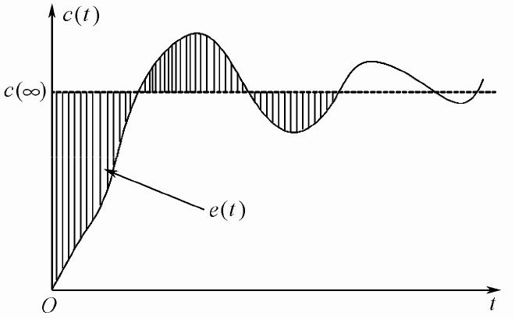
图5.2　阶跃响应误差指标图

有如下几种常用的误差积分指标。

（1）误差积分指标IE。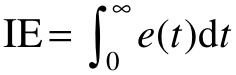，显然，该指标对于振荡型过程不适用。

（2）误差绝对值积分指标IAE。。

（3）误差平方积分指标ISE。。

后两种指标均用于振荡型响应分析，其中ISE指标比较适合在理论分析中使用。一般来说，在同等条件下，用ISE指标设计出来的系统与用IAE指标设计出来的系统相比较，其tr较小而σp%较大。

（4）误差绝对值乘时间积分指标ITAE。。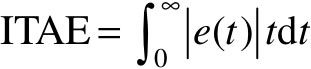

由图5.2可以看出，IAE和ISE指标的大小主要取决于第一块面积，但在一般情况下，系统的相对稳定性σp%和综合快速性ts由第二块面积的大小来反映，因此应加上第二块在指数函数中的份额，处理方法是乘以时间函数t作为权系数。该指标目前被广泛应用于最优化分析和设计中。

5.2.4　一阶和二阶系统的时域响应

5.2.4.1　一阶系统时域响应

可以用一阶微分方程描述的系统称为一阶系统，其传递函数为：

式中，T称为一阶系统的时间常数，G(s)可写成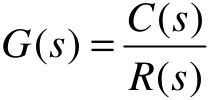。当r(t)=1(t)，即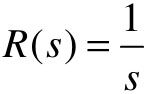时，一阶系统的输出c(t)称为单位阶跃响应，其拉氏变换式为

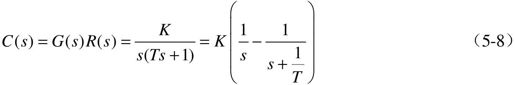
对式（5-8）进行拉氏反变换，得

典型的一阶系统的单位阶跃响应曲线如图5.3所示。

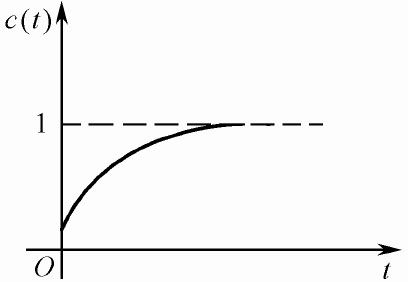
图5.3　一阶系统的单位阶跃响应曲线

一阶系统时域响应的性能指标如下。

（1）调整时间ts：经过时间3T～4T，响应曲线已达稳态值的95%～98%，可以认为其调整过程已完成，故一般取ts=(3～4)T。

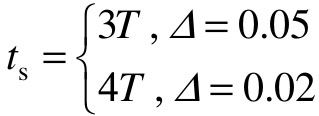
2）稳态误差ess：系统的实际输出c(t)在时间t趋于无穷大时将趋近输入值，即

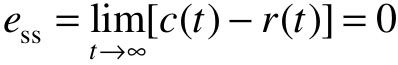
（3）超调量σp%：一阶系统的单位阶跃响应为非周期响应，是单调的，故系统无振荡、无超调，σp%=0。

一阶系统的闭环极点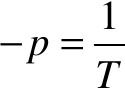，位于实轴上，由此可得到以下两条结论：

• 如果系统闭环极点位于负实轴上，则阶跃响应是单调的，σp%=0。
• 调节时间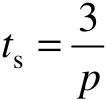，即闭环极点离虚轴距离越远则响应越快。

5.2.4.2　二阶系统时域响应

典型二阶系统的结构如图5.4所示，其闭环传递函数G(s)为：

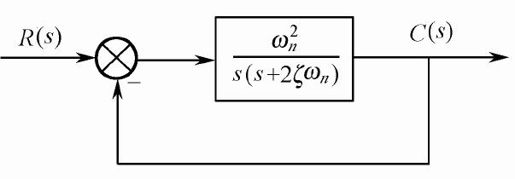
图5.4　典型二阶系统的结构图

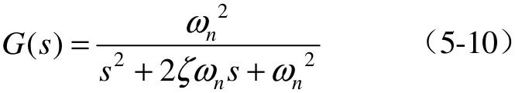
或

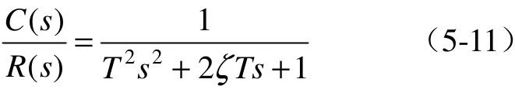
式中，ωn为无阻尼自由振荡角频率，简称固有频率；ζ为阻尼系数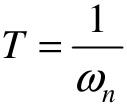；为系统振荡周期。

系统的特征方程为：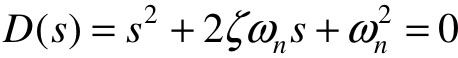

特征根为：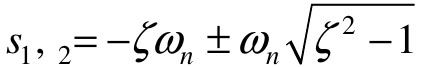

因此，二阶系统的两个极点为：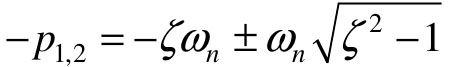

在不同阻尼比下两个极点有不同的特征，因此其时域响应特征也不同。

1. 零阻尼（ζ=0）

此时两个极点是一对纯虚根，-p1,2=±jωn，可求得其单位阶跃响应为：

典型的单位阶跃响应曲线如图5.5所示，是一种等幅振荡曲线，振荡角频率就是ωn。

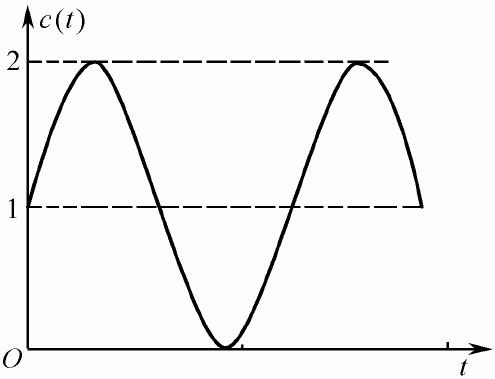
图5.5　零阻尼系统单位阶跃响应曲线

1. 欠阻尼（0<ζ<1）

此时两个极点是一对负实部的共轭复根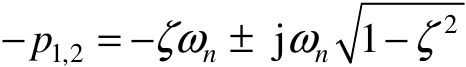，，典型的单位阶跃响应如图5.6所示，是一种衰减振荡曲线。

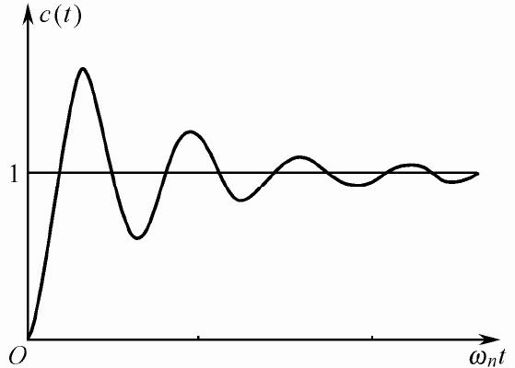
图5.6　欠阻尼系统单位阶跃响应曲线

曲线的表达式可表示为：

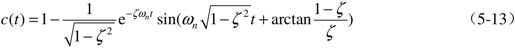
通常可设σ=ζωn为衰减指数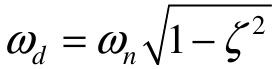；为振荡角频率；为初相角。

其他性能指标可用以下方法求取。

（1）上升时间tr。由c(t)|t=tr=1，得到即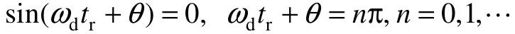，由于第一次达到稳态值的时间取n=1，则

（2）峰值时间tp。令可得到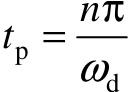，由于第一次达到的峰值取n=1，则

（3）超调量σp%。由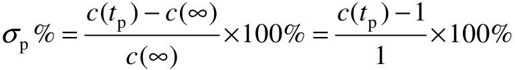可得到：

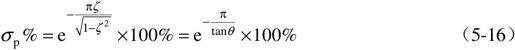
（4）超调时间ts。按定义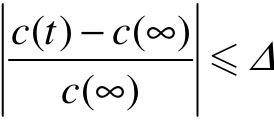，即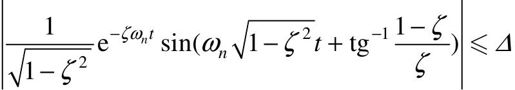，由于正弦项的绝对值总小于1，故上式可近似地表示为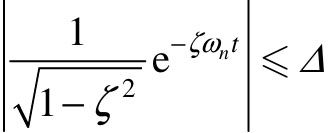：，即。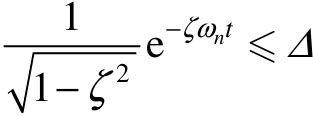

由于上述不等式是单调下降的，取等号即可，故经化简可得：

在常用的ζ范围（0.4～0.9）内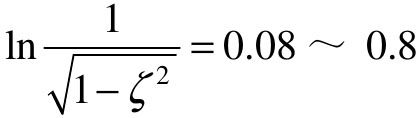，，平均取0.5是合适的，故

1. 临界阻尼（ζ=1）

此时两个极点是一对负实数重极点，-p1,2=-ωn，其单位阶跃响应表达式可表示为：

典型的单位阶跃响应如图5.7所示。

图5.7　临界阻尼系统单位阶跃响应曲线

由图可见，ζ=1时，阶跃响应正好进入单调无超调状态（σp%=0），故可从这个意义上定义其临界。临界阻尼下的调节时间可以通过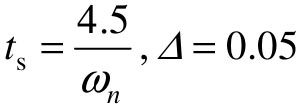计算来获得。

1. 过阻尼（ζ>1）

此时两个极点是两个不相等的负实数极点，。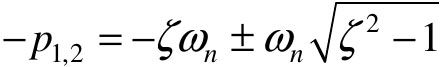

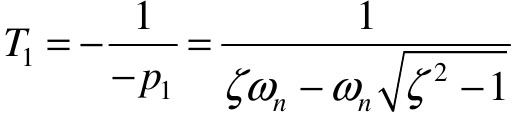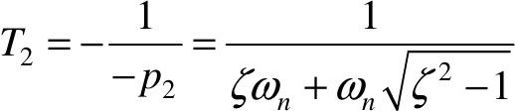和，则

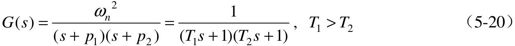
其单位阶跃响应表达式可表示为：

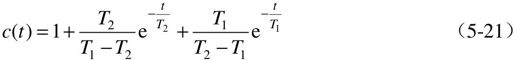
典型的单位阶跃响应曲线如图5.8所示。

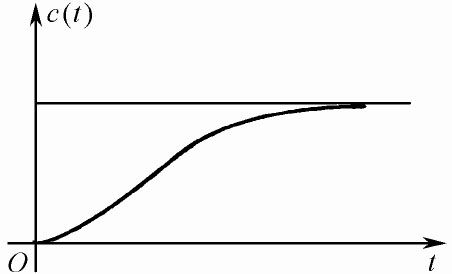
图5.8　过阻尼系统单位阶跃响应曲线

从图可以看出，响应仍是一个单调过程，σp%=0，其调节时间ts可通过数值计算来确定，ζ越大，即T1和T2越错开，ts越大。

从图中可以看出一个重要现象，即当T1>>T2时，对响应表达式中的两个分量，只有第二分量（与T1对应）起主要作用，而第一分量（与T2对应）仅仅影响时域响应的起始点。一般认为，当T1>>5T2时，T2的影响就可以忽略不计了，即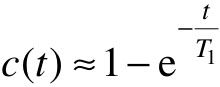，相应地

此时二阶系统就可以近似地作为一阶系统来分析了。

5.2.5　高阶系统的时域分析

5.2.5.1　高阶系统时域响应的一般形式

设系统的闭环传递函数为：

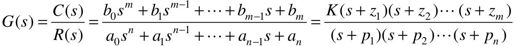
当输入r(t)=1(t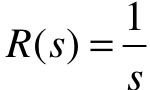)时，，此时

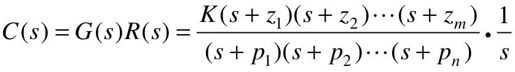
为使问题简单化一些，可设G(s)中无重极点，则

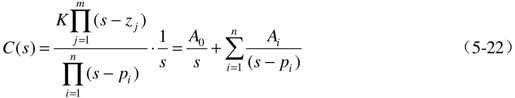
式中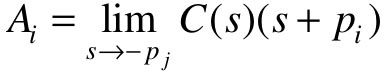，，i=0,1,…,n,-p0=0，则

一般地，若G(s)的极点中有q个负实数极点、r个负实部共轭复数极点，则上式还可改写为：

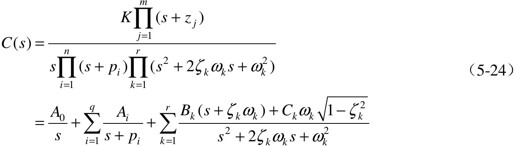
式中，r+2q=m，则

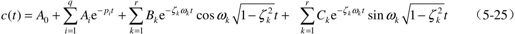
5.2.5.2　高阶系统的主导极点

由式（5-25）可知，高阶系统阶跃响应是由一系列动态分量组成的，各动态分量的幅值由闭环极点和零点共同决定。

由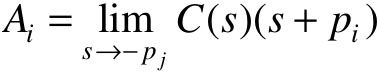可知，当某个极点与某个零点接近时，其幅值必定很小，其动态分量的衰减速度由其极点的实部，即闭环极点距虚轴的距离决定。距虚轴越远的闭环极点，其所对应的动态分量衰减越快。显然，在阶跃响应过程中，影响最大的分量是那些幅值最大而衰减又最慢的分量，这些分量所对应的闭环极点是那些距虚轴最近而附近又没有闭环零点的闭环极点。

由此可得以下结论：

（1）主导极点。在整个响应过程中，起决定性作用的是闭环极点，称之为主导极点，它是距虚轴最近而附近又没有闭环零点的闭环极点。工程上往往只用主导极点来估算系统的动态特性，即将系统近似地看成是一阶或二阶系统。

（2）距虚轴的距离较主导极点远5倍或5倍以上的闭环零点、极点，其影响可以忽略不计。

（3）偶极子。一对靠得很近的闭环零点、极点称为偶极子。工程上，当某极点与某零点之间的距离比它们的模值小一个数量级时，就可认为这对零点、极点为偶极子。偶极子对时域的影响可以忽略不计。在闭环传递函数中，如果零点、极点数值上相近，则可将该零点和极点一起消掉，称为偶极子相消。

（4）除主导极点外，闭环零点的作用是使响应加快而超调增加，闭环极点的作用则正好相反。